 Intégrales
Intégrales
A SAVOIR: le cours sur les intégrales
Exercice 10
Cet exercice utilise primitives et intégrales.Quadrature de la parabole par la méthode d'Archimède
Nous allons déterminer l'aire délimitée par une portion de parabole en utilisant deux méthodes différentes.
Considérons une parabole $P $. Nous pouvons alors munir le plan d'un repère orthonormé tel que cette parabole $P $ soit la représentation graphique d'un trinôme $f$ défini sur $\ℝ$ par $f(x)=mx^2$, où $m$ est un paramètre strictement positif fixé (plus $m$ est proche de 0, plus la parabole est "aplatie").
Cette propriété est admise.
Soit $a$ et $b$ deux nombres fixés (avec $a\< b$).
Soit A le point de $P $ d'abscisse $a$ et B le point de $P $ d'abscisse $b$.
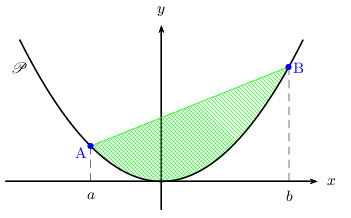
Nous allons déterminer l'aire $A_D$ du domaine $D$ (hachuré en vert) délimité par le segment [AB] et la parabole $P $
Méthode 1
-
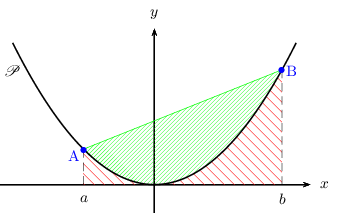
On admet que $b^3-a^3=(b-a)(a^2+ab+b^2)$.
Montrer, en utilisant une primitive, que l'aire $A_r$ du domaine (hachuré en rouge) situé entre $P $, l'axe des abscisses, et les droites d'équation $x=a$ et $x=b$ vérifie:
$A_r=m(b-a){a^2+ab+b^2}/{3}$ -
Chacun sait que l'aire d'un trapèze est donnée par la formule ${(base+Base)}/{2}×hauteur$.
Montrer que l'aire $A_t$ du trapèze constitué de la réunion des domaines hachurés en rouge et en vert vérifie:
$A_t=m(b-a){a^2+b^2}/{2}$ -
Montrer que l'aire $A_D$ du domaine $D$ (hachuré en vert) vérifie $A_D=m{(b-a)^3}/{6}$.
On notera que cette aire dépend uniquement de $m$ (lié à la forme de la parabole) et de la distance entre $a$ et $b$.
Méthode 2
Nous allons retrouver cette aire en utilisant la méthode géométrique employée par Archimède.
Pour simplifier, nous allons moderniser la méthode en utilisant quelques raisonnement analytiques.
Mais il faut savoir qu'Archimède (III éme siècle avant JC) a procédé de façon purement géométrique, les concepts de coordonnées et de fonction lui étant totalement inconnus.
-
Préambule
A est le point de $P $ d'abscisse $a$.
On pose $b=a+2h$.
Donc B est le point de $P $ d'abscisse $a+2h$.
On définit alors C comme le point de $P $ d'abscisse $a+h$.
Et soit M le milieu de la corde [AB].
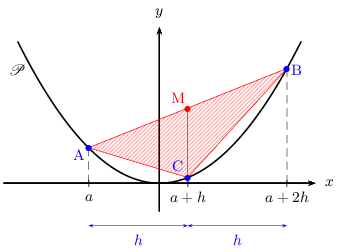
a. Vérifier que $x_M=a+h$ et $y_M=m{2a^2+4ah+4h^2}/{2}$
b. On a: $MC=y_M-y_C$. Montrer que $MC=mh^2$.
c. Chacun sait que l'aire d'un triangle est donnée par la formule ${base×hauteur}/{2}$.
Montrer que l'aire du triangle AMC vaut $m{h^3}/{2}$.
d. Montrer que l'aire du triangle ABC (hachuré en rouge) vaut $mh^3$.
On notera que cette aire dépend uniquement de $m$ (lié à la forme de la parabole) et de la demi-distance $h$ entre $a$ et $b$.
Cette aire peut aussi s'écrire $s_0=m{(b-a)^3}/{8}$ -
On pose $b=a+4h$ et on reprend le graphique précédent sur lequel on a ajouté les points D et E de la parabole $P $.
Cette fois-ci: A a pour abscisse $a$, D a pour abscisse $a+h$, C a pour abscisse $a+2h$, E a pour abscisse $a+3h$ et B a pour abscisse $a+4h$.
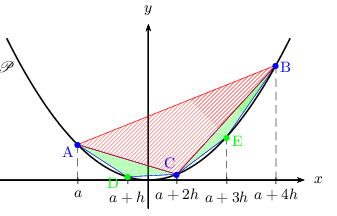
En utilisant le préambule, exprimer les aires des triangles ADC et CEB (hachurés en vert) en fonction de $h$ et de $m$.
Vérifier que la somme $s_1$ de leurs aires vérifie: $s_1=m{(b-a)^3}/{32}$ - On considère alors le domaine égal au polygone ADCEB constitué des triangles ABC, ADC et CEB.
Montrer que l'aire du polygone ADCEB vaut $A_1=m{(b-a)^3}/{8}(1+{1}/{4})$. -
En posant $b=a+8h$, on peut réitérer le processus précédent avec 4 points supplémentaires, les points F, G, H et I du graphique ci-dessous.
On obtient 4 triangles de plus (hachurés en bleu).
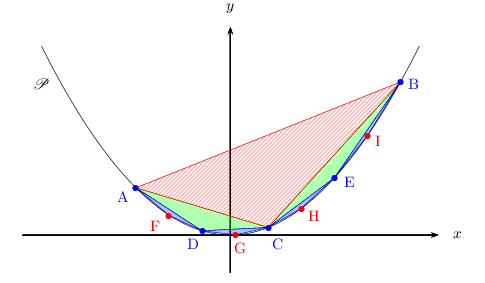
On peut alors montrer que l'aire du polygone AFDGCHEIB vaut $m{(b-a)^3}/{8}(1+{1}/{4}+{1}/{4^2})$.
En réitérant autant de fois que nécessaire ce processus, on obtient un polygone $P_n$ dont l'aire vaut $A_n=m{(b-a)^3}/{8}(1+{1}/{4}+{1}/{4^2}+...+{1}/{4^n})$ (où $n$ est un entier naturel non nul).
Montrer que $A_n=m{(b-a)^3}/{6}(1-0,25×0,25^n)$ -
Déterminer $\lim↙{n→+∞}A_n$
- On constate que, quand $n$ grandit, le polygone $P_n$ se rapproche de plus en plus de l'arc de parabole.
On admet que lorsque $n$ tend vers $+∞$, l'aire $A_n$ du polygone $P_n$ tend vers l'aire $A_D$ du domaine $D$ délimité par le segment [AB] et la parabole $P $.
Retrouver le résultat obtenu avec la première méthode.
Corrigé
Dans cet exercice, il est clair que tous les points d'abscisse $x$ situés sur la parabole ont une ordonnée égale à $mx^2$. Cela sera considéré comme une évidence.
Méthode 1
- La fonction $f$ étant clairement continue et positive sur $[a;b]$, l'aire cherchée vaut:
$A_r=∫_a^b f(x)dx=∫_a^b mx^2dx=[m{x^3}/{3}]_a^b=m{b^3}/{3}-m{a^3}/{3}=m{b^3-a^3}/{3}$
Or: $b^3-a^3=(b-a)(a^2+ab+b^2)$.
Donc: $A_r=m(b-a){a^2+ab+b^2}/{3}$ -
Le trapèze constitué de la réunion des domaines hachurés en rouge et en vert a pour dimensions:
$base=f(a)=ma^2$, $Base=f(b)=mb^2$ et $hauteur=b-a$.
Son aire est donc égale à: $A_t={ma^2+mb^2}/{2}×(b-a)$
Soit: $A_t=m(b-a){a^2+b^2}/{2}$ -
Or l'aire $A_D$ est la différence de l'aire du trapèze et de l'aire du domaine sous la parabole.
Donc: $A_D=A_t-A_r$
Soit: $A_D=m(b-a){a^2+b^2}/{2}-m(b-a){a^2+ab+b^2}/{3}=m(b-a)({a^2+b^2}/{2}-{a^2+ab+b^2}/{3})$
Soit: $A_D=m(b-a)({3a^2+3b^2}/{6}-{2a^2+2ab+2b^2}/{6})$
Soit: $A_D=m(b-a){3a^2+3b^2-2a^2-2ab-2b^2}/{6}$
Soit: $A_D=m(b-a){a^2+b^2-2ab}/{6}$
Soit: $A_D=m(b-a){(b-a)^2}/{6}$
Soit: $A_D=m{(b-a)^3}/{6}$
Méthode 2
-
Préambule

a. M est le milieu de [AB]. Donc $x_M={x_A+x_B}/{2}$ et $y_M={y_A+y_B}/{2}$
Donc: $x_M={a+a+2h}/{2}$ et $y_M={ma^2+m(a+2h)^2}/{2}$
Soit: $x_M={2(a+h)}/{2}$ et $y_M=m{a^2+a^2+4ah+4h^2}/{2}$
Soit: $x_M=a+h$ et $y_M=m{2a^2+4ah+4h^2}/{2}$
b. On a: $MC=y_M-y_C=m{2a^2+4ah+4h^2}/{2}-m(a+h)^2$
Soit: $MC=m{2a^2+4ah+4h^2-2(a+h)^2}$
Soit: $MC=m{2a^2+4ah+4h^2-2a^2-4ah-2h^2}/{2}$
Soit: $MC=m{2h^2}/{2}$
Soit: $MC=mh^2$
c. Le triangle AMC a pour base MC et pour hauteur $h$.
Son aire vaut donc: ${MC×h}/{2}$
Soit: ${mh^2×h}/{2}$.
Finalement, le triangle AMC a pour aire: $m{h^3}/{2}$.
d. Le triangle ABC (hachuré en rouge) est constitué des triangles AMC et BMC.
Comme ces deux triangles ont la même base MC et la même hauteur $h$, ils ont la même aire.
On calcule alors: $2×m{h^3}/{2}=mh^3$
Par conséquent, le triangle ABC a pour aire $mh^3$
Comme $b=a+2h$, il est clair que $h={b-a}/2$.
Cette aire peut donc aussi s'écrire $s_0=m{(b-a)^3}/{8}$
L'intérêt de cette écriture est qu'elle ne dépend que de $m$, $a$ et $b$. -

Les triangles ADC et CEB sont inscrits dans la parabole. Or $y_C-y_A=2h$ et $y_B-y_C=2h$. Dons, d'après le préambule, les triangles ADC et CEB ont chacun pour aire: $mh^3$.
La somme de leurs aires vaut donc: $s_1=2mh^3$.
Et comme $h={b-a}/{4}$, on obtient: $s_1=2m({b-a}/{4})^3$
Soit: $s_1=m{(b-a)^3}/{32}$
- On considère le domaine égal au polygone ADCEB constitué des triangles ABC, ADC et CEB.
Or l'aire de ABC vaut $s_0=m{(b-a)^3}/{8}$.
Et la somme $s_1$ des aires de ADC et CEB vaut: $s_1=m{(b-a)^3}/{32}$.
Donc l'aire du polygone ADCEB vaut $A_1=s_0+s_1$
Mais attention! Nous devons utiliser les expressions de $s_0$ et $s_1$ en fonction de $m$, $a$ et $b$, et non pas celles qui sont fonction de $m$ et $h$ (en effet, la valeur de $h$ change entre les 2 expressions).
On obtient donc: $A_1=m(b-a)^3({1}/{8}+{1}/{32})$
Soit: $A_1=m{(b-a)^3}/{8}(1+{1}/{4})$
- On a: $A_n=m{(b-a)^3}/{8}(1+{1}/{4}+{1}/{4^2}+...+{1}/{4^n})$ (où $n$ est un entier naturel non nul).
Soit: $A_n=m{(b-a)^3}/{8}(1+0,25+0,25^2+...+0,25^n)$
Soit: $A_n=m{(b-a)^3}/{8}{1-0,25^{n+1}}/{1-0,25}$
Soit: $A_n=m{(b-a)^3}/{8}{1-0,25×0,25^n}/{0,75}$
Soit: $A_n=m{(b-a)^3}/{8×0,75}(1-0,25×0,25^n)$
Et donc: $A_n=m{(b-a)^3}/{6}(1-0,25×0,25^n)$ - On rappelle que, si $0$<$ q$<$1$, alors $\lim↙{n→+∞}q^n=0$
Ici: $q=0,25$
On obtient alors: $\lim↙{n→+∞}A_n= m{(b-a)^3}/{6}(1-0,25×0)$
Soit: $\lim↙{n→+∞}A_n=m{(b-a)^3}/{6}$ -
On admet que lorsque $n$ tend vers $+∞$, l'aire $A_n$ du polygone $P_n$ tend vers l'aire $A_D$ du domaine $D$ délimité par le segment [AB] et la parabole $P $.
Par conséquent, la limite trouvée correspond à l'aire du domaine $D$.
Donc l'aire $A_D$ du domaine $D$ vérifie $A_D=m{(b-a)^3}/{6}$.
On a retrouvé le résultat obtenu avec la première méthode.