 Intégrales
Intégrales
A SAVOIR: le cours sur les intégrales
Exercice 9
Cet exercice utilise primitives et intégrales.Soit $f$ définie sur $[1,4]$ par $f(x)=5\ln x-2$, représentée par $\C$.
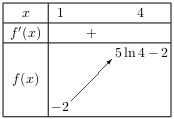
- Déterminer $f\,'$, puis le signe de $f\,'$, et dresser le tableau de variation de $f$ sur $[1,4]$.
- Montrer que $f$ est strictement positive sur $[2;4]$.
- Pourquoi $f$ est-elle continue sur $[2;4]$?
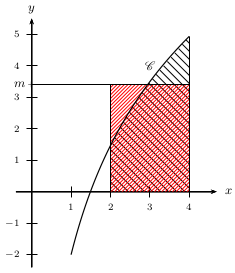
- Tracer rapidement $\C$ sur $[1;4]$.
- Montrer que $x\ln x-x$ est une primitive de $\ln x$ sur $]0;+∞[$.
- En déduire une primitive $F$ de la fonction $f$ sur $[2,4]$.
-
Soit $A$ l'aire du domaine situé entre $C$, l'axe des abscisses, les droites d'équation $x=2$ et $x=4$.
Montrer que $A=30\ln2-14$. - Calculer $m$, valeur moyenne de $f$ entre 2 et 4. Interpréter graphiquement.
Corrigé
-
$f\,'(x)=5{1}/{x}-0={5}/{x}$.
Or, ${5}/{x}$ est strictement positif pour $x$ strictement positif.
Donc $f\,'$ est strictement positive sur $[1,4]$.
D'où le tableau de variation de $f$.
-
Soit $x$ dans l'intervalle $[2;4]$. Donc on a, en particulier $2\text"<"x$.
Comme $f$ est strictement croissante, on obtient: $f(2)\text"<"f(x)$.
Or, $f(2)≈1,4$ est strictement positif.
Donc, on obtient: $0\text"<"f(x)$.
Donc $f$ est strictement positive sur $[2;4]$. - $f$, dérivable sur $[2;4]$, y est donc continue.
-
Valeurs à 0,001 près

-
Posons $G(x)=x\ln x-x$ et $g(x)=\ln x$. Dérivons $G$.
On pose: $G=uv-x$ avec $u=x$, $v=\ln x$, $u'=1$, $v'={1}/{x}$.
On a: $G'=u'v+uv'-1$.
Soit: $G'(x)=1×\ln x+x×{1}/{x}-1=\ln x+1-1=\ln x=g(x)$.
Donc $G'=g$ sur $ ]0;+∞[$.
Et donc $x\ln x-x$ est une primitive de $\ln x$ sur $]0;+∞[$. -
$f=5g-2$; donc, par exemple: $F=5G-2x$ est une primitive de $f$.
Soit $F(x)=5(x\ln x-x)-2x=5x\ln x-7x$. -
Comme $f$ est continue et positive sur $[2;4]$, on a: $$A=∫_2^4 f(x)dx$$.
Soit: $$A=F(4)-F(2)=(20\ln 4-28)-(10\ln2-14)=20\ln2^2-28-10\ln2+14$$.
Soit: $$A=40\ln2-10\ln2-14=30\ln2-14$$.
-
$$m={1}/{4-2}∫_2^4 f(x)dx={1}/{2}(30\ln2-14)=15\ln2-7≈3,4$$.
C'est aussi l'aire du rectangle de côtés 2 et $m$ hachuré en rouge.