Suites numériques, modèles discrets
A SAVOIR: le cours sur les suites
Exercice 3
Soit $f$ la fonction définie pour tout réel $x$ par $f(x)=4-0,1x^2$.
$f$ est représentée par la parabole $\P$ ci-dessous.
On a également dessiné la droite $d$ d'équation $y=x$.
Soit $(u_n)$ la suite définie, pour tout naturel $n$, par $u_{n+1}=f(u_n)$
et par: $u_0=5$.
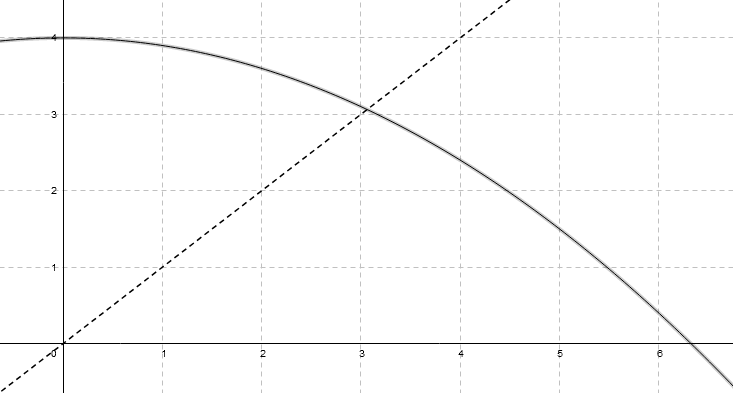
Déterminer l'abscisse $l$ du point d'intersection de la droite $d$ et de la parabole $\P$ dont l'abscisse est positive.
Reproduire ce graphique, puis y représenter $u_0$, $u_1$, $u_2$, $u_3$ et $u_4$.
Conjecturer la valeur de $\lim↙{n→+∞}(u_n)$.
Corrigé
Clique ICI pour relire la partie du cours à réviser.
L'abscisse cherchée vérifie $ 4-0,1l^2=l$.
Soit: $0=0,1l^2+l-4$
On a là un trinôme, avec $a=0,1$, $b=1$ et $c=-4$.
On a alors: $Δ=b^2-4ac=1^2-4×0,1×(-4)==2,6$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={-1-√{2,6}}/{0,2}=-5-√{65}≈-13,1$ et $x_2={-b+√Δ}/{2a}=-5+√{65}≈3,1$.
Comme l'abscisse cherchée est positive, on obtient: $l=-5+√{65}≈3,1$.
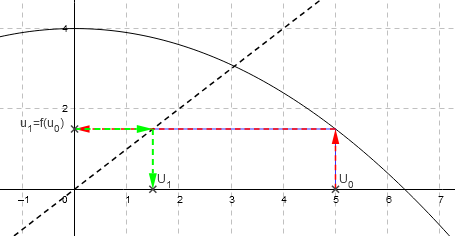
$u_0$ est placé sur le graphique.
On cherche alors $u_1=f(u_0)$ sur l'axe des ordonnées.
On reporte cette valeur sur l'axe des abscisses grace à la droite $d$.
Et on réitère la construction pour obtenir $u_2$, $u_3$ et $u_4$.
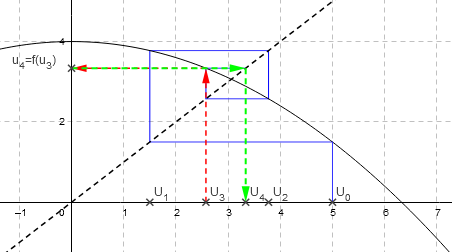
On conjecture alors que $\lim↙{n→+∞}(u_n)=l=-5+√{65}≈3,1$