Suites numériques, modèles discrets
A SAVOIR: le cours sur les suites
Exercice 6
1.a. Eva emprunte à sa banque $1\,000$ euros au taux annuel de $2\%$. Elle va rembourser en 2 fois. Une première fois 500 euros au bout d'un an. Une seconde fois $x$ euros deux ans après le début du prêt.
Expliquer pourquoi Eva doit encore 520 euros après son premier remboursement.
1.b. Combien vaut $x$?
1.c. Vanessa emprunte à sa banque $1\,000$ euros au taux annuel de $2\%$. Elle va rembourser en 2 fois. Une première fois $s$ euros au bout d'un an. Une seconde fois $s$ euros deux ans après le début du prêt.
Montrer que $s=1\,040,40-1,02s$
Combien vaut $s$?
L'amortissement d'un emprunt est la partie du capital qui est remboursée à chaque échéance périodique (par exemple chaque mois).
Ce paiement se fait en même temps que celui des intérêts dus pour la même période.
Le versement total (amortissement + intérêts) à chaque échéance est dénommé, selon sa périodicité, la mensualité, trimestrialité ou annuité.
On considère un prêt, d'un montant (capital) égal à $C$, au taux mensuel égal à $t$.
Chaque mois, l'emprunteur rembourse le même montant, égal à $M$.
Après $n$ mensualités, le prêt est supposé totalement remboursé.
On appelle $u_i$ le capital restant dû après $i$ mensualités. On a donc $u_0=C$ et $u_n=0$.
2.a. Montrer que $u_1=C×(1+t)-M$.
2.b. Montrer que $u_{2}=C(1+t)^2-M(1+t)-M$.
2.c. Montrer que $u_{3}=C(1+t)^3-M(1+t)^2-M(1+t)-M$.
2.d. On admet que, pour tout entier $i$ entre 1 et $n$, on a: $u_{i}=C(1+t)^i-M(1+t)^{i-1}-M(1+t)^{i-2}-...-M(1+t)^2-M(1+t)-M$.
Expliquer pourquoi on a: $u_{i}=C(1+t)^i-M{(1+t)^{i}-1}/{t}$.
Montrer que: $M=C{t(1+t)^n}/{(1+t)^{n}-1}$
3.a. Emma a emprunté sur deux ans $1\,200$ euros au taux de $0,1\%$ par mois.
Elle rembourse en 24 mensualités égales à $M$ euros chacune.
Combien vaut $M$ (arrondie à $0,01$ euro)?
Par la suite, il est conseillé d'utiliser la valeur exacte de M dans les calculs pour éviter de propager des erreurs dues aux approximations.
3.b. Quel est le coût total du crédit?
3.c. Quel est le capital restant dû au bout d'un an (après 12 mensualités)?
3.d. Quel est le montant total des intérêts versés à la banque au bout de la première année?
Le comparer à celui des intérêts versés au cours de la seconde année.
4. Noémie a emprunté sur deux ans $C$ euros au taux de $0,1\%$ par mois.
Elle rembourse en 24 mensualités égales à $50$ euros chacune.
Combien vaut $C$?
Corrigé
Clique ICI pour revoir l'essentiel sur les suites géométriques.
1.a. Au bout d'un an, avant de verser le premier remboursement, le capital dû par Eva est égal à: $1\,000×(1+0,02)=1\,020$ euros.
Après son premier remboursement de 500 euros, Eva doit encore $1\,020-500=$$520$ euros .
1.b. Au bout de deux ans, avant de verser le second remboursement, le capital dû par Eva est égal à: $520×(1+0,02)=530,40$ euros.
Comme elle rembourse $x$ euros, et qu'elle ne doit alors plus rien, on a: $x=530,40$ euros.
1.c. Au bout d'un an, avant de verser le premier remboursement, le capital dû par Vanessa est égal à: $1\,000×(1,02)=1\,020$ euros.
Après son premier remboursement de $s$ euros, Vanessa doit encore $1\,020-s$ euros.
Au bout de deux ans, avant de verser le second remboursement, le capital dû par Vanessa est égal à: $(1\,020-s)×(1,02)=1\,040,40-1,02s$ euros.
Comme elle rembourse $s$ euros, et qu'elle ne doit alors plus rien, on a: $s=1\,040,40-1,02s$
Donc: $2,02s=1\,040,40$
Et donc: $s={1\,040,40}/{2,02}≈$$515,05$ euros.
2.a. Au bout d'un mois, avant de verser la mensualité, le capital dû est égal à: $C×(1+t)$.
Après versement de la mensualité, le capital dû est égal à: $C×(1+t)-M$.
Donc: $u_1=C×(1+t)-M$.
2.b. Au bout de 2 mois, avant de verser la mensualité, le capital dû est égal à: $u_1×(1+t)$.
Après versement de la mensualité, le capital dû est égal à: $u_1×(1+t)-M$.
Or: $u_1=C×(1+t)-M$.
Donc: $u_2=(C×(1+t)-M)×(1+t)-M$
Soit: $u_2=C(1+t)^2-M(1+t)-M$. c.q.f.d.
2.c. De même, on obtient: $u_3=u_2×(1+t)-M$
Or: $u_2=C(1+t)^2-M(1+t)-M$
Donc: $u_2=(C(1+t)^2-M(1+t)-M)×(1+t)-M$
Soit: $u_{3}=C(1+t)^3-M(1+t)^2-M(1+t)-M$. c.q.f.d.
2.d. On a: $u_{i}=C(1+t)^i-M(1+t)^{i-1}-M(1+t)^{i-2}-...-M(1+t)^2-M(1+t)-M$.
On factorise M, d'où: $u_{i}=C(1+t)^i-M((1+t)^{i-1}+(1+t)^{i-2}+...+(1+t)^2+(1+t)+1)$.
On obtient alors: $u_{i}=C(1+t)^i-M{1-(1+t)^{i-1+1}}/{1-(1+t)}$.
Soit, en multipliant numérateur et dénominateur par $-1$:
$u_{i}=C(1+t)^i-M{(1+t)^{i}-1}/{t}$. c.q.f.d.
En particulier, on a: $u_{n}=C(1+t)^n-M{(1+t)^{n}-1}/{t}$.
Et comme $u_n=0$, on obtient: $0=C(1+t)^n-M{(1+t)^{n}-1}/{t}$.
Donc: $M{(1+t)^{n}-1}/{t}=C(1+t)^n$.
Soit: $M=C{t(1+t)^n}/{(1+t)^{n}-1}$ c.q.f.d.
3.a. Emma a emprunté sur deux ans $1\,200$ euros au taux de $0,1\%$ par mois.
Elle rembourse en 24 mensualités égales à $M$ euros chacune.
Ici: $C=1\,200$,
$t=0,001$, et $n=24$.
Donc: $M=1\,200{0,001×1,001^{24}}/{1,001^{24}-1}≈$$50,63$
Chaque mensualité vaut environ $50,63$ euros.
3.b. On calcule: $24M-C=24{1\,200{0,001(1,001)^{24}}/{(1,001)^{24}-1}-1\,200≈15,06$
Le coût total du crédit est d'environ 15,06 euros.
3.c. On calcule: $u_{12}=C(1+t)^{12}-M{(1+t)^{12}-1}/{t}≈1\,200×1,001^{12}-M{1,001^{12}-1}/{0,001}≈603,60$.
Le capital restant dû au bout d'un an est d'environ 603,60 euros.
3.d. On calcule: $C-u_{12}≈1\,200-603,60≈596,40$.
Au bout d'un an, le capital remboursé est d'environ 596,40 euros.
On calcule donc: $12M-596,40≈11,13$
Le montant total des intérêts versés au bout de la première année est donc d'environ 11,13 euros.
On calcule alors: $15,06-11,13≈3,93$
Le montant total des intérêts versés au cours de la seconde année est donc d'environ 3,93 euros.
Les intérêts sont donc surtout versés la première année!
Avec des échéances constantes, le rapport ${\text"capital amorti"}/{\text"intérêts versés"}$ augmente au cours du temps.
Cela se voit parfaitement dans le tableau d'amortissements ci-dessous (regarder les 2 dernières colonnes).
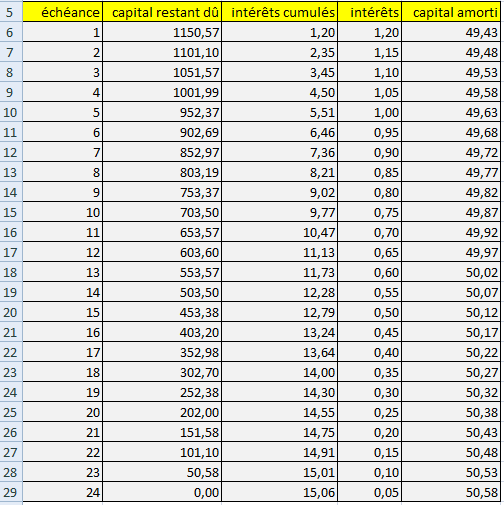
4. Noémie a emprunté sur deux ans $C$ euros au taux de $0,1\%$ par mois.
Elle rembourse en 24 mensualités égales à $50$ euros chacune.
On a: $M=C{t(1+t)^n}/{(1+t)^{n}-1}$, et donc: $50=C{0,001×1,001^{24}}/{1,001^{24}-1}$
Et par là: $C={50×(1,001^{24}-1)}/{0,001×1,001^{24}}≈$$1185,13$
Noémie a emprunté environ $1185,13$ euros