 Nombres complexes
Nombres complexes
I Point de vue algébrique
Définitions et propriétés
L'ensemble $\ℂ$ des nombres complexes est tel que:
- $\ℝ$ est inclus dans $\ℂ$
- Les règles de calcul dans $\ℝ$ se prolongent à $\ℂ$
- Le nombre complexe $i$ vérifie $i^2=-1$
-
Tout nombre complexe $z$ s'écrit de manière unique sous la forme algébrique
$z=x+iy$, avec $x$ et $y$ réels.
$x$, partie réelle de $z$, se note $\Re(z)$.
$y$, partie imaginaire de $z$, se note $\Im(z)$. - ${z}↖{−}=x-iy$ est le conjugué de $z=x+iy$.
- Un complexe de partie réelle nulle s'appelle un imaginaire pur.
 Exemple
Exemple
Ecrire les nombres complexes suivants sous forme algébrique:
- $z=(2+3i)(4-i)$
- $z=(2-3i)^2$
- $$z={2+3i}/{1-i}$$
Corrigé
-
$z=(2+3i)(4-i)=2×4-2×i+3i×4-3i×i=8-2i+12i-3×i^2$
Soit: $z=8+10i-3×(-1)=8+10i+3=11+10i$. - $z=(2-3i)^2=2^2-2×2×3i+(3i)^2=4-12i+9i^2=4-12i-9=-5-12i$.
-
Pour éliminer le $i$ au dénominateur, on utilise le conjugué de ce dénominateur.
$$z={2+3i}/{1-i}={(2+3i)(1+i)}/{(1-i)(1+i)}={2+2i+3i+3i^2}/{1^2-i^2}= {2+5i-3}/{1-(-1)}={-1+5i}/{2}=-0,5+2,5i$$
Ces calculs sont vérifiables à la calculatrice en "mode complexe".
Casio: Touche OPTN, puis valider le "mode complexe" CPLX par F3.
TI: Sélectionner le mode a+$i$b.
Propriété d'identification
Deux complexes sont égaux si et seulement si ils ont même partie réelle et même partie imaginaire.
A retenir
La propriété d'identification est très pratique pour résoudre certaines équations.
 Exemple
Exemple
Déterminer le complexe $a$ sachant que $(a-1)+i(a+1)=2+3i$.
Corrigé
Ecrivons $a$ sous forme algébrique; on pose $a=x+iy$, avec $x$ et $y$ réels.
On a alors: $(x+iy-1)+i(x+iy+1)=2+3i$
Soit: $x+iy-1+ix+i^2y+i=2+3i$
Soit: $x+iy-1+ix-y+i=2+3i$
Soit: $(x-1-y)+i(y+x+1)=2+3i$
Par unicité de la forme algébrique, on obtient:
$\{\table x-1-y=2; y+x+1=3$
Soit: $\{\table x-y=3; x+y=2$
Soit: $\{\table x=2,5; y=-0,5$
Et par là: $a=2,5-0,5i$
 Exemple
Exemple
Résoudre sur $\ℂ$ l'équation $z^2+2i{z}↖{−}-6=0$.
Il est conseillé d'écrire $z$ sous forme algébrique,
puis de déterminer un système équivalent à l'équation initiale.
Corrigé
Posons $z=x+iy$ avec $x$ et $y$ réels.
On a alors: $z^2+2i{z}↖{−}-6= (x+iy)^2+2i(x-iy)-6=x^2-y^2+2y-6+2ix(y+1)$
Donc: $z^2+2i{z}↖{−}-6=0 ⇔ x^2-y^2+2y-6+2ix(y+1)=0+0i$
Donc: $z^2+2i{z}↖{−}-6=0 ⇔\{\table x^2-y^2+2y-6=0; 2x(y+1)=0$
On a remplacé une équation dans $\ℂ$ par un système dans $\ℝ$.
On a donc: $z^2+2i{z}↖{−}-6=0 ⇔\{\table x^2-y^2+2y-6=0; 2x=0$
ou $\{\table x^2-y^2+2y-6=0; y+1=0$
Soit: $z^2+2i{z}↖{−}-6=0 ⇔\{\table y^2-2y+6=0; x=0$
ou $\{\table x^2-9=0; y=-1$
Résolvons tout d'abord le premier système.
Le trinôme $ y^2-2y+6$ a pour discriminant $\Δ=(-2)^2-4 ×1 ×6=-20$.
Comme $\Δ\text"<"0$, ce trinôme n'a pas de racines réelles, et par là, le premier système n'a pas de solution.
Résolvons ensuite le second système.
Le trinôme $x^2-9$ a pour racines -3 et 3.
Par ailleurs, on constate que $y=-1$.
Conclusion:
On obtient finalement: $z^2+2i{z}↖{−}-6=0 ⇔\{\table x=-3; y=-1$
ou $\{\table x=3; y=-1$
On rappelle alors que l'on a posé $z=x+iy$ avec $x$ et $y$ réels.
L'équation initiale a donc 2 solutions complexes: $-3-i$ et $3-i$.
Propriétés
Si $z$ est un nombre complexe, alors:
$${{z}↖{−}}↖{−}=z$$ $$z+{z}↖{−}=2\Re(z)$$ $$z-{z}↖{−}=2i\Im(z)$$.$z∈\ℝ ⇔z={z}↖{−}$ $z$ est un imaginaire pur $⇔z=-{z}↖{−}$.
Définition
Soient $z$ et $z'$ deux nombres complexes avec $z≠0$.
L'inverse de $z$ est le nombre complexe $Z$ tel que $z×Z=1$; on le note ${1}/{z}$.
Le quotient de $z'$ par $z$ se note ${z'}/{z}$ et vérifie ${z'}/{z}=z'×{1}/{z}$.
 Exemple
Exemple
Déterminons (sans calculatrice) la forme algébrique de l'inverse de $z=3+2i$.
Nous allons utiliser le conjugué ${z}↖{−}=3-2i$.
On écrit: ${1}/{z}={1}/{3+2i}={1×(3-2i)}/{(3+2i)×(3-2i)}={3-2i}/{3^2-4i^2}={3-2i}/{9+4}$
Soit: ${1}/{z}={3}/{13}-{2}/{13}i$.
C'est la forme algébrique de l'inverse de $z$.
Opérations
Si $z$ et $z'$ sont 2 nombres complexes et si $n$ est un entier naturel non nul, alors:
$$\ov{z+z'}={z}↖{−}+\ov{z'}$$ $$\ov{zz'}={z}↖{−}\ov{{z'}$$ $$\ov{{z^n}}={{z}↖{−}}^n$$.$$\ov{({1}/{z})}={1}/{{z}↖{−}}$$ (pour $z$ non nul) $$\ov{({z}/{z'})}={{z}↖{−}}/{\ov{z'}}$$ (pour $z'$ non nul)
 Exemple
Exemple
Déterminer la forme algébrique de $c=\ov{iz}+{z+2\Re{z}-{z}↖{−}}/{iz}$ pour $z=2+3i$.
Corrigé
$c=\ov{iz}+{2\Re{z}+(z-{z}↖{−})}/{iz}={i}↖{−}{z}↖{−}+{{2(\Re{z}+i\Im{z})}/{iz}=-i{z}↖{−}+{{2z}/{iz}=-i{z}↖{−}+{{2}/{i}$
Soit: $c=-i(2-3i)+{2i}/{i^2}=-2i+3i^2-2i=-2i-3-2i=-3-4i$
Formule du binôme dans $\ℂ$
Soient $z$ et $z'$ deux nombres complexes, et $n$ un entier naturel non nul.
$$(z+z')^n=z^n+(\table n;1)z^{n-1}×z'+(\table n;2)z^{n-2}×z'^2+...+(\table n;n-1)z×z'^{n-1}+z'^n$$
On écrit aussi: $$(z+z')^n=∑↙{k=0}↖n (\table n;k)z^{n-k}×z'^k$$
 Exemple
Exemple
Déterminons (sans calculatrice) la forme algébrique de $z=(3+2i)^4$.
On écrit: $$(3+2i)^4=∑↙{k=0}↖4 (\table 4;k)3^{4-k}×(2i)^k$$
Soit: $(3+2i)^4=3^4+(\table 4;1)3^3×2i+(\table 4;2)3^2×(2i)^2+(\table 4;3)3×(2i)^3+(2i)^4$
Soit: $(3+2i)^4=81+4×27×2i+6×9×(-4)+4×3×(-8i)+16$
Soit: $(3+2i)^4=81+216i-216-96i+16$
Soit: $(3+2i)^4=-119+120i$
C'est la forme algébrique demandée.
II Point de vue géométrique
Définition
Le plan complexe est le plan muni d'un répère orthonormal direct $(O,I,J)$.
A tout nombre complexe $z=x+iy$, avec $x$ et $y$ réels, on associe le point M de coordonnées $(x;y)$.
M est le point image de $z$.
${OM}↖{→}$ est le vecteur image de $z$.
$z$ est l'affixe du point M et du vecteur ${OM}↖{→}$.
L'axe des abscisses s'appelle aussi l'axe des réels.
L'axe des ordonnées s'appelle aussi l'axe des imaginaires purs.
Propriété
Deux vecteurs sont égaux ( ou deux points sont confondus) si et seulement si leurs affixes sont égales.
Propriété
Si $k$ est un réel, et si ${u}↖{→}$ et ${v}↖{→}$ sont deux vecteurs d'affixes respectives $z$ et $z'$,
alors ${u}↖{→}+{v}↖{→}$ a pour affixe $z+z'$,
et $k{u}↖{→}$ a pour affixe $kz$.
Propriété
Si A et B sont deux points du plan complexe d'affixes respectives $z_A$ et $z_B$,
alors le vecteur ${AB}↖{→}$ a pour affixe $$z_B-z_A$$,
et le milieu du segment $[AB]$ a pour affixe $${z_A+z_B}/{2}$$.
 Exemple
Exemple
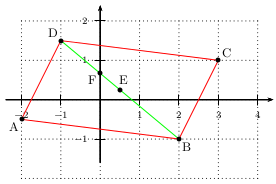
Dans le plan complexe, A, B et D sont 3 points
d'affixes respectives $z_A=-2-0,5i$, $z_B=2-i$ et $z_D=-1+1,5i$.
Déterminer l'affixe $z_C$ du point C tel que ABCD soit un parallélogramme.
Déterminer l'affixe $z_E$ du centre E de ABCD.
Soit F point d'affixe $z_F={2}/{3}i$. Montrer que B, D et F sont alignés.
Faire une figure et vérifier ces résultats.
Corrigé
ABCD est un parallélogramme$⇔{AB}↖{→}={DC}↖{→}⇔z_B-z_A=z_C-z_D$
Donc: ABCD est un parallélogramme$⇔2-i-(-2-0,5i)=z_C-(-1+1,5i)$
Donc: ABCD est un parallélogramme$⇔2-i+2+0,5i-1+1,5i=z_C$
Donc: ABCD est un parallélogramme$⇔3+i=z_C$
Par conséquent, C a pour affixe $3+i$.
Le centre E du parallélogramme ABCD est le milieu de ses diagonales, par exemple de $[BD]$.
Donc $z_E={z_B+z_D}/{2}={2-i+(-1+1,5i)}/{2}={1+0,5i}/{2}=$$0,5+0,25i$.
${BD}↖{→}$ a pour affixe: $z_{{BD}↖{→}}=z_D-z_B=-1+1,5i-(2-i)=-1+1,5i-2+i=-3+2,5i$,
${BF}↖{→}$ a pour affixe: $z_{{BF}↖{→}}=z_F-z_B={2}/{3}i-(2-i)={2}/{3}i-2+i=-2+{5}/{3}i$,
On constate que: $z_{{BD}↖{→}}={3}/{2}z_{{BF}↖{→}}$, et donc que: ${BD}↖{→}={3}/{2}{BF}↖{→}$.
Par conséquent, les vecteurs ${BD}↖{→}$ et ${BF}↖{→}$ étant colinéaires,
les points B, D et F sont alignés.
Tout se vérifie sur la figure ci-dessous.
Propriété
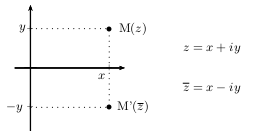
Dans le plan complexe, 2 points d'affixes conjuguées sont symétriques par rapport à l'axe des abscisses.
Définition et propriété
Le plan est rapporté au repère (O,I,J).
Lorsque l'on gradue la tangente $d$ en I au cercle trigonométrique $\C$ avec la même unité que le plan (selon le dessin qui suit),
et que l'on enroule la droite des réels obtenue sur $\C$, chaque réel $α$ de $d$ est associé à un unique point M de $\C$.
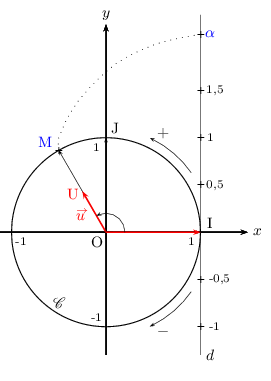
Soit ${u}↖{→}$ un vecteur tels que ${u}↖{→}={OU}↖{→}$.
Soit M le point d'intersection du cercle trigonométrique $\C$ et de la droite (OU).
Si $α$ est un réel de $d$ associé au point point M de $\C$,
alors $α$ est une mesure en radians de l'angle orienté $({OI}↖{→};{u}↖{→})$.
Et l'ensemble des mesures possibles est alors $\{α+2kπ, k∈ℤ\}$.
On notera: $({OI}↖{→};{u}↖{→})=α\, [2 π] $
Propriété
Si ${u}↖{→}$ et ${v}↖{→}$ sont deux vecteurs du plan tels que $({OI}↖{→};{u}↖{→})=α\, [2 π] $ et $({OI}↖{→};{v}↖{→})=β\, [2 π]$,
alors $({u}↖{→};{v}↖{→})=β-α\, [2 π] $
Définition
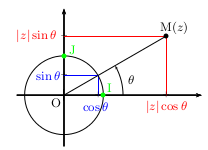
Soit $z$ un nombre complexe de forme algébrique $x+iy$.
Le module de $z$ est le nombre réel positif, noté $|z|$,
défini par $$|z|=√{x^2+y^2}$$.
Si, dans le plan complexe muni du repère (O,I,J), $z$ a pour point image M,
alors $$OM=|z|$$;
et si $z$ est non nul,
alors son argument, noté $\arg z$, est n'importe quelle mesure (en radians)
de l'angle orienté $({OI}↖{→};{OM}↖{→})$;
et si l'on pose $\arg z=θ\, [2 π]$,
alors on obtient une forme trigonométrique de $z$:
$$z=|z|(\cos θ+i\sin θ)$$.
Propriété
Si $z$ est un nombre complexe, alors:
$$z{z}↖{−}=|z|^2$$
Si $z$ et $z'$ sont 2 nombres complexes, alors, ils vérifient l'inégalité triangulaire:
Propriété
Si $z$ est un nombre complexe, $r$ un réel strictement positif, et $θ$ un réel, alors:
$z=r(\cos θ+i\sin θ)$ $⇔$ $|z|=r$ et $\arg z=θ\, [2 π]$ Exemple
Exemple
On pose $z=1-i√{3}$.
Déterminer le module et un argument de $z$. Ecrire $z$ sous forme trigonométrique.
Corrigé
$|z|=√{1^2+(-√{3})^2}=√{1+3}=2$
On factorise: $z=2({1}/{2}-i{√{3}}/{2})$.
On note alors que: $z=2(\cos (-{π}/{3})+i\sin (-{π}/{3}))$.
C'est l'écriture de $z$ sous forme trigonométrique.
Par conséquent: $\arg z=-{π}/{3}\, [2 π]$.
Propriétés
Si $z$ est un nombre complexe non nul, alors:
$$|-z|=|z|$$ $$\arg(-z)=\arg z+π\, [2 π]$$$$|{z}↖{−}|=|z|$$ $$\arg({z}↖{−})=-\arg z\, [2 π]$$.
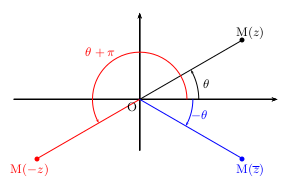
$z∈\ℝ⇔\arg(z)=0\,[2 π]$ ou $\arg(z)=π\,[2 π]$.
$z$ est imaginaire pur si et seulement si $\arg(z)={π}/{2}\,[2 π]$ ou $\arg(z)=-{π}/{2}\,[2 π]$.
Opérations
Si $z$ et $z'$ sont 2 nombres complexes non nuls et si $n$ est un entier naturel, alors:
$$|zz'|=|z||z'|$$ $$\arg(zz')=\arg z+\arg z'\, [2 π]$$$$|{z}/{z'}|={|z|}/{|z'|}$$ $$\arg({z}/{z'})=\arg z-\arg z'\, [2 π]$$
$$|z^n|=|z|^n$$ $$\arg(z^n)=n\arg z\, [2 π]$$
 Exemple
Exemple
Soit $z=1+i$ et $z'=√3-i$.
Déterminer modules et arguments de $z$ et de $z'$.
Trouver une forme trigonométrique de $zz'$.
En déduire la valeur exacte de $\cos {π}/{12}$ et $\sin ({π}/{12})$.
Corrigé
$|z|=√{1^2+1^2}=√2$
On factorise: $z=√2({1}/{√2}+i{1}/{√2})=√2({√2}/{2}+i{√2}/{2})$.
On note alors que: $z=√2(\cos ({π}/{4})+i\sin ({π}/{4}))$.
C'est l'écriture de $z$ sous forme trigonométrique.
Par conséquent: $\arg z={π}/{4}\, [2 π]$.
$|z'|=√{(√3)^2+(-1)^2}=√4=2$
On factorise: $z'=2({√3}/{2}-i{1}/{2})$.
On note alors que: $z'=2(\cos (-{π}/{6})+i\sin (-{π}/{6}))$.
C'est l'écriture de $z'$ sous forme trigonométrique.
Par conséquent: $\arg z'=-{π}/{6}\, [2 π]$.
Et par là, on obtient:
$|zz'|=|z||z'|=√2×2=2√2$.
$\arg(zz')=\arg z+\arg z'={π}/{4}+(-{π}/{6})={3π-2π}/{12}={π}/{12}\, [2 π]$.
Donc, $zz'$ admet pour forme trigonométrique: $2√2(\cos {π}/{12}+\sin {π}/{12})$.
Or: $zz'=(1+i)(√3-i)=√3-i+i√3-i^2=√3-i+i√3+1=√3+1+(√3-1)i$.
Soit: $zz'=2√2({√3+1}/{2√2}+{√3-1}/{2√2}i)$.
Par conséquent, on obtient finalement: $\cos {π}/{12}={√3+1}/{2√2}$ et $\sin {π}/{12}={√3-1}/{2√2}$.
Définition
L'ensemble des nombres complexes de module 1 se note $U$.
Propriété
L'ensemble $U$ est représenté par le cercle de centre O et de rayon 1 (appelé cercle unité)
Cet ensemble est stable par produit et par passage à l'inverse, c'est à dire que:
Si $z$ et $z'$ sont dans $U$, alors $zz'$ et ${z}/{z'}$ sont également dans $U$.
 Exemple
Exemple
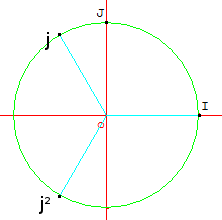
On pose $j=-{1}/{2}+{√{3}}/{2}i$.
Montrons que $j$ est dans $U$, puis que $j^2$ est aussi dans $U$.
On calcule: $|j|^2=(-{1}/{2})^2+({√{3}}/{2})^2={1}/{4}+{3}/{4}=1$.
Donc: $|j|=1$, et par là: $j$ appartient à $U$.
Et, comme $U$ est stable par produit, $j^2$ est aussi dans $U$.
$j$ et $j^2$ sont représentés ci-dessous.
III Trigonométrie
Formules d'addition
Soient $a$ et $b$ deux nombres réels
$\cos(a+b)=\cos a \cos b -\sin a \sin b$$\cos(a-b)=\cos a \cos b +\sin a \sin b$
$\sin(a+b)=\sin a \cos b +\cos a \sin b$
$\sin(a-b)=\sin a \cos b -\cos a \sin b$
Formules de duplication
Soient $a$ un nombre réel
$\cos(2a)=\cos^2 a -\sin^2 a=1-2\sin^2 a=2\cos^2 a-1$$\sin 2a=2\sin a \cos a $
 Exemple
Exemple
- A l'aide d'une formule d'addition, déterminer la valeur de $\cos { 7π}/{12}$
- A l'aide d'une formule de duplication, déterminer la valeur de $\sin { π}/{8}$
Corrigé
On tente de faire apparaître des angles remarquables.
-
On note que: $ { 7π}/{12}= { π}/{4}+ { π}/{3}$.
Par conséquent: $\cos { 7π}/{12}=\cos { π}/{4} \cos { π}/{3} -\sin { π}/{4} \sin { π}/{3}$
Soit: $\cos { 7π}/{12}={√{2}}/{2} ×{1}/{2} -{√{2}}/{2} ×{√{3}}/{2}$
Soit: $\cos { 7π}/{12}={√{2}-√{6}}/{4}$ -
On note que: $ 2{ π}/{8}= { π}/{4}$.
Par conséquent: $\cos{ π}/{4}=1-2\sin^2 { π}/{8}$
Soit: ${√{2}}/{2}=1-2\sin^2 { π}/{8}$
Et par là: $\sin^2 { π}/{8}={2-√{2}}/{4}$
Donc: $\sin { π}/{8}=√{{2-√{2}}/{4}}$ ou $\sin { π}/{8}=-√{{2-√{2}}/{4}}$
Mais, comme $0<{ π}/{8}≤{ π}/{2}$, on a: $\sin { π}/{8}>0$.
Par conséquent: $\sin { π}/{8}=√{{2-√{2}}/{4}}$
Soit: $\sin { π}/{8}={√{2-√{2}}}/{2}$
Définition
Soit $z$ un nombre complexe non nul dont un argument est $θ$.
Une forme exponentielle de $z$ est l'écriture $$z=|z|e^{iθ}$$,
où $e^{iθ}$ désigne le nombre complexe de module 1 et dont un argument est $θ$.
Ainsi: $$e^{iθ}=\cos θ+i \sin θ$$
Propriétés
Si $θ$ et $θ'$ sont 2 nombres réels et si $n$ est un entier naturel, alors:
$$|e^{iθ}|=1$$ $$\arg(e^{iθ})=θ\, [2 π]$$$$e^{iθ}×e^{iθ'}=e^{i(θ+θ')}$$ $$(e^{iθ})^n=e^{inθ}$$ (formule de Moivre)
$${1}/{e^{iθ}}=e^{-iθ}=\ov {e^{iθ}} $$ $${e^{iθ}}/{e^{iθ'}}=e^{i(θ-θ')}$$
$$e^{iθ}=e^{iθ'}⇔θ=θ'\, [2 π]$$
 Exemple
Exemple
Soit $z={1+i√3}/{1+i}$.
Ecrire $z$ sous forme exponentielle.
Calculer $z^{30}$.
Corrigé
$|1+i√3|=√{1^2+(√3)^2}=√4=2$
On factorise: $1+i√3=2({1}/{2}+i{√3}/{2})$.
On note alors que: $1+i√3=2(\cos ({π}/{3})+i\sin ({π}/{3}))=2e^{i{π}/{3}}$.
$|1+i|=√{1^2+1^2}=√2$
On factorise: $1+i=√2({1}/{√2}+i{1}/{√2})=√2({√2}/{2}+i{√2}/{2})$.
On note alors que: $1+i=√2(\cos ({π}/{4})+i\sin ({π}/{4}))=√2e^{i{π}/{4}}$.
D'où: $z={2e^{i{π}/{3}}}/{√2e^{i{π}/{4}}}=√2e^{i({π}/{3}-{π}/{4})}=√2e^{i{π}/{12}$.
Et finalement: $z^{30}=(√2)^{30}e^{i{30π}/{12}}=2^{15}e^{i{5π}/{2}$.
Et comme ${5π}/{2}={π}/{2}\, [2 π]$, on obtient: $z^{30}=2^{15}e^{i{π}/{2}}=2^{15}i$.
Formules d'Euler
Soit $θ$ un nombre réel
$\cos θ={e^{iθ}+e^{-iθ}}/{2}$ $\sin θ={e^{iθ}-e^{-iθ}}/{2i}$ Exemple
Exemple
Soit $θ$ un réel. Linéariser $\cos^3 θ$.
Linéariser une puissance de cosinus ou de sinus, c'est l'écrire sous forme d'une somme de cosinus ou de sinus uniquement.
Corrigé
On a: $\cos θ={e^{iθ}+e^{-iθ}}/{2}$ (d'après les formules d'Euler)
Donc: $\cos^3 θ=({e^{iθ}+e^{-iθ}}/{2})^3={(e^{iθ}+e^{-iθ})^3}/{8}$
On applique alors la formule du binôme de Newton.
On obtient: $\cos^3 θ={(e^{iθ})^3+3(e^{iθ})^2e^{-iθ}+3e^{iθ}(e^{-iθ})^2+(e^{-iθ})^3}/{8}$
Soit: $\cos^3 θ={e^{i3θ}+3e^{i2θ}e^{-iθ}+3e^{iθ}e^{-i2θ}+e^{-i3θ}}/{8}$
Soit: $\cos^3 θ={e^{i3θ}+3e^{iθ}+3e^{-iθ}+e^{-i3θ}}/{8}$
On regroupe les termes pour utiliser à nouveau les formules d'Euler.
On obtient: $\cos^3 θ={e^{i3θ}+e^{-i3θ}+3(e^{iθ}+e^{-iθ})}/{8}$
Donc: $\cos^3 θ={2\cos 3θ+6\cosθ}/{8}$
Soit: $\cos^3 θ={1}/{4}\cos 3θ+{3}/{4}\cosθ$
A retenir
Si l'on écrit des complexes sous leur forme exponentielle,
alors il est beaucoup plus facile de les multiplier entre eux, d'en faire des quotients, ou de les élever à une certaine puissance.
IV Equations polynomiales
Dans ce qui suit, les polynômes considérés seront des polynômes sur $\ℂ$ à coefficient réels (sauf indication contraire).
Définition
Soit $a$ un nombre réel.
Les solutions dans $\ℂ$ de l'équation $z^2=a$ sont appelées racines carrées de $a$ dans $\ℂ$.
Propriété
Soit $a$ un nombre réel.
Si $a=0$,
alors $a$ admet exactement 1 racine carrée dans $\ℂ$: le nombre 0.
Si $a\text">"0$,
alors $a$ admet exactement 2 racines carrées dans $\ℂ$: les réels $√a$ et $-√a$.
Si $a\text"<"0$,
alors $a$ admet exactement 2 racines carrées dans $\ℂ$:
les imaginaires purs $i√{-a}$ et $-i√{-a}$.
Exemple
Quelles sont les racines carrées dans $\ℂ$ de -3?
Ce sont les imaginaires purs $i√{-(-3)}=i√3$ et
$-i√{-(-3)}=-i√3$.
Equation du second degré à coefficients réels
Soit $a$, $b$ et $c$ trois réels avec $a≠0$.
On considère l'équation $az^2+bz+c=0$ dont on cherche les racines dans $\ℂ$.
L'équation a pour discriminant $Δ=b^2-4ac$.
- Si $Δ=0$, alors l'équation a 1 unique solution, le réel ${-b}/{2a}$.
- Si $Δ\text">"0$, alors l'équation a 2 solutions, les réels ${-b-√Δ}/{2a}$ et ${-b+√Δ}/{2a}$.
- Si $Δ\text"<"0$, alors l'équation a 2 solutions, les complexes conjugués ${-b-i√{-Δ}}/{2a}$ et ${-b+i√{-Δ}}/{2a}$.
Propriété
Soit $a$, $b$ et $c$ trois réels avec $a≠0$.
Soient $z_1$ et $z_2$ les racines de l'équation $az^2+bz+c=0$ (avec éventuellement $z_1=z_2$.
Le trinôme se factorise alors sous la forme: $az^2+bz+c=a(z-z_1)(z-z_2)$.
 Exemple
Exemple
Résoudre dans $\ℂ$ chacune des équations suivantes, puis factoriser le trinôme correspondant.
$3z^2-z-2=0$.
$z^2-z+1=0$.
$z^2+3=0$.
Corrigé
$3z^2-z-2$ est un trinôme à coefficients réels.
Avec les notations usuelles:$a=3$, $b=-1$ et $c=-2$.
$Δ=b^2-4ac=1-(-24)=25$.
$Δ\text">"0$, donc l'équation a 2 solutions dans $\ℂ$:
les réels ${-b-√Δ}/{2a}={1-5}/{6}={-2}/{3}$ et
${-b+√Δ}/{2a}={1+5}/{6}=1$.
$\S=\{{-2}/{3};1\}$.
On a alors: $3z^2-z-2=3(z-{-2}/{3})(z-1)=3(z+{2}/{3})(z-1)$.
$z^2-z+1$ est un trinôme à coefficients réels.
Avec les notations usuelles:$a=1$, $b=-1$ et $c=1$.
$Δ=b^2-4ac=1-4=-3$.
$Δ\text"<"0$, donc l'équation a 2 solutions dans $\ℂ$:
les complexes conjugués ${-b-i√{-Δ}}/{2a}={1-i√{3}}/{2}={1}/{2}-i{√{3}}/{2}$ et
${-b+i√{-Δ}}/{2a}={1+i√{3}}/{2}={1}/{2}+i{√{3}}/{2}$.
$\S=\{{1}/{2}-i{√{3}}/{2};{1}/{2}+i{√{3}}/{2}\}$.
On a alors: $z^2-z+1=3(z-({1}/{2}-i{√{3}}/{2}))(z-({1}/{2}+i{√{3}}/{2}))=3(z-{1}/{2}+i{√{3}}/{2})(z-{1}/{2}-i{√{3}}/{2})$.
$z^2+3$ est un trinôme à coefficients réels, dont les racines dans $\ℂ$ sont , de façon évidente, les racines carrées dans $\ℂ$ de -3.
C'est à dire $-i√3$ et $i√3$.
$\S=\{-i√3;i√3\}$.
On a alors: $z^2-z+1=1(z-(-i√3))(z-i√3)=(z+i√3)(z-i√3)$.
Savoir faire
Attention!
Les résultats proposés sur les équations du second degré ne concernent que les équations du second degré à coefficients réels.
Si l'un des trois coefficients n'est pas réel, alors le signe du discriminant n'a plus de sens, et les résultats ne sont plus valides (voir exercice 2 (question 4) sur les complexes).
Propriété
Soit $a$ et $z$ deux nombres complexes, et $n$ un entier naturel non nul.
Le polynôme $z^n-a^n$ se factorise alors sous la forme: $z^n-a^n=(z-a)(z^{n-1}+az^{n-2}+a^2z^{n-3}+...+a^{n-2}z+a^{n-1})$.
Remarque: les polynômes cités ici sont éventuellement à coefficients complexes.
 Exemple
Exemple
Factoriser le polynôme complexe $z^5+i$
Corrigé
Comme $(-i)^5=-i$, on a: $z^5+i=z^5-(-i)^5$
Et donc: $z^5+i=(z-(-i))(z^4+(-i)z^3+(-i)^2z^2+(-i)^3z+(-i)^4)$
Soit: $z^5+i=(z+i)(z^4-iz^3-z^2+iz+1)$
Propriété
Si $P(z)$ est un polynôme, et si $P(a)=0$, alors $P(z)$ est factorisable par $z-a$,
C'est à dire qu'il existe un polynôme $Q(z)$ tel que $P(z)=(z-a)Q(z)$.
La somme du degré de Q et de 1 est alors égale au degré de P.
Remarque: les polynômes $z-a$ et $Q(z)$ sont éventuellement à coefficients complexes.
Propriété
Soit $n$ un entier naturel non nul.
Un polynôme de degré $n$ admet au plus $n$ racines.
 Exemple
Exemple
Déterminer les racines du polynôme $p(z)=z^3+2z^2-1$ (il est conseillé de repérer d'abord une racine évidente)
Corrigé
Une racine évidente est à chercher entre 0, 1, -1, 2, -2, i et -i.
Posons $z=-1$. On calcule: $z^3+2z^2-1=-1+2-1=0$.
Donc $-1$ est racine de $p(z)$.
Donc $p(z)$ est factorisable par $z+1$, et on a: $p(z)=(z+1)Q(z)$, où Q sera de degré 2.
Posons $Q(z)=az^2+bz+c$.
On obtient alors: $p(z)=(z+1)(az^2+bz+c)$
Soit: $z^3+2z^2-1=az^3+(b+a)z^2+(c+b)z+c$
Et comme deux polynômes égaux ont les mêmes coefficients, on obtient:
$\{\table 1=a;2=b+a;0=c+b;-1=c$
Et par là: $a=1$ $b=1$ $c=-1$
Et donc: $p(z)=(z+1)(z^2+z-1))$
On trouve alors facilement les racines de $z^2+z-1$.
Ce sont: ${-1-√5}/{2}$ et ${-1+√5}/{2}$
Par conséquent, les racines de $p(z)$ sont: $-1$, ${-1-√5}/{2}$ et ${-1+√5}/{2}$.
V Applications géométriques
Interprétation géométrique
Soit A, B et C trois points d'affixes respectives $z_A$, $z_B$ et $z_C$ dans le plan complexe muni d'un répère orthonormal direct $(O,I,J)$.
$$AB=|z_B-z_A|$$$$\arg(z_B-z_A)=({OI}↖{→};{AB}↖{→})\, [2 π]$$ pour A et B distincts.
$${AC}/{AB}=|{z_C-z_A}/{z_B-z_A}|$$ pour A et B distincts .
$$\arg({z_C-z_A}/{z_B-z_A})=({AB}↖{→};{AC}↖{→})\, [2 π]$$ pour A et B distincts et A et C distincts.
 Exemple
Exemple
Soit A d'affixe $-1$,
B d'affixe $√3-1+i$
et C d'afffixe $√2-1+yi$ (avec $y$ réel strictement positif).
ABC est isocèle en A.
Déterminer la valeur de $y$.
Déterminer une mesure de l'angle $({AB}↖{→};{AC}↖{→})$.
En déduire que $\tan {π}/{12}={√{6}-√{2}}/{√{2}+√{6}}$.
Corrigé
ABC est isocèle en A,donc: $AB=AC$.
Or: $AB=|z_B-z_A|=|√3-1+i+1|=|√3+i|=√{{√3}^2+1^2}=√4=2$.
Et: $AC=|z_C-z_A|=|√2-1+yi+1|=|√2+yi|=√{{√2}^2+y^2}=√{2+y^2}$.
Donc: $AB=AC⇔2=√{2+y^2}⇔4=2+y^2⇔2=y^2$.
Et comme $y$ est un réel strictement positif, on obtient: $AB=AC ⇔y=√{2}$.
Finalement: $ y=√{2}$.
On est tenté de déterminer $\arg {z_C-z_A}/{z_B-z_A}$.
On calcule donc: ${z_C-z_A}/{z_B-z_A}={√2-1+√{2}i+1}/{√3-1+i+1}={√2+√{2}i}/{√3+i}={(√2+√{2}i)×(√3-i)}/{(√3+i)×(√3-i)}$
Soit: ${z_C-z_A}/{z_B-z_A}={√{2}+√{6}+i(√{6}-√{2})}/{4}$
L'argument n'est pas évident. On préfère alors décomposer.
On a alors:
$({AB}↖{→};{AC}↖{→})=({AB}↖{→};{OI}↖{→})+({OI}↖{→};{AC}↖{→})=({OI}↖{→};{AC}↖{→})-({OI}↖{→};{AB}↖{→})$.
Soit: $({AB}↖{→};{AC}↖{→})=\arg(z_C-z_A)-\arg(z_B-z_A)$
Or: $z_C-z_A=√2-1+√2i+1=√2+√2i$.
Et on a vu que: $|z_C-z_A|=|z_B-z_A|=2$.
On factorise: $z_C-z_A=2({√2}/{2}+i{√2}/{2})$.
On note alors que: $z_C-z_A=2(\cos ({π}/{4})+i\sin ({π}/{4}))$.
C'est l'écriture de $z_C-z_A$ sous forme trigonométrique.
Par conséquent: $\arg (z_C-z_A)={π}/{4}\, [2 π]$.
De même, on obtient: $z_B-z_A=2({√3}/{2}+i{1}/{2})$.
On note alors que: $z_B-z_A=2(\cos ({π}/{6})+i\sin ({π}/{6}))$.
C'est l'écriture de $z_B-z_A$ sous forme trigonométrique.
Par conséquent: $\arg (z_B-z_A)={π}/{6}\, [2 π]$.
Par conséquent, on obtient finalement: $({AB}↖{→};{AC}↖{→})={π}/{4}-{π}/{6}={π}/{12}\, [2 π]$.
Une mesure de l'angle $({AB}↖{→};{AC}↖{→})$ est ${π}/{12}$.
Le calcul initial peut alors servir!
En effet, on a trouvé que: ${z_C-z_A}/{z_B-z_A}={√{2}+√{6}+i(√{6}-√{2})}/{4}={√{2}+√{6}}/{4}+i{√{6}-√{2}}/{4}$
Or $\arg {z_C-z_A}/{z_B-z_A}={π}/{12}\, [2 π]$.
Par conséquent: $\tan {π}/{12}={√{6}-√{2}}/{√{2}+√{6}}$
Définition
Soit $n$ un entier naturel non nul.
On appelle racine n-ième de l'unité tout complexe $z$ tel que $z^n=1$.
Propriété
Soit $n$ un entier naturel non nul.
L'équation $z^n=1$ admet exactement $n$ racines n-ième de l'unité.
Ce sont les complexes de la forme $e^{i{2kπ}/{n}}$ où $k$ est un entier entre 0 et $n-1$.
L'ensemble des racines n-ièmes de l'unité se note $U_n$
Propriété
Soit $n$ un entier naturel non nul.
Les images des éléments de $U_n$ appartiennent toutes au cercle unité. Elles forment un polygone régulier à $n$ côtés (pour $n≥3$)