 Matrices et graphes
Matrices et graphes
Merci à F.L. pour son aide précieuse.
Dans tout ce qui suit, sauf indication contraire, $n$ et $p$ sont deux entiers naturels non nuls.
I Les matrices
a. Généralités
Définitions
Une matrice d'ordre $(n;p)$ (ou de dimension $n×p$) est un "tableau" de nombres à $n$ lignes et $p$ colonnes.
Une matrice s'inscrit entre des parenthèses.
Chaque élément de la matrice est appelé coefficient.
Si $n=1$, alors la matrice est une "matrice ligne".
Si $p=1$, alors la matrice est une "matrice colonne".
L'ensemble de toutes les matrices d'ordre $(n;p)$ à coefficients réels se note $M_{n,p}(ℝ)$.
 Exemple
Exemple
$P=(\table 1, 0.2,1, 2)$ est une matrice ligne.
$Q=(\table 0.35;6;0.6;0.06)$ est une matrice colonne.
$R=(\table 0.8,0.15,0.7,1.5;1,0.2,1,2;1.6,0.35,1.8,4.5)$ est une matrice d'ordre $(3;4)$ (ou de dimension $3×4$).
Définition
Une matrice d'ordre $(n;n)$ (ou de dimension $n×n$) s'appelle une matrice carrée d'ordre $n$.
L'ensemble de toutes les matrices d'ordre $n$ à coefficients réels peut se noter $M_{n}(ℝ)$.
 Exemple
Exemple
$B=(\table 1, {1}/{3};4,-{5}/{3})$ est une matrice carrée d'ordre 2.
$B$ appartient à l'ensemble $M_{2}(ℝ)$.
Définition
Si A est une matrice d'ordre $(n;p)$, alors le coefficient de A situé à la ligne $i$ et à la colonne $j$ se note $a_{ij}$.
 Exemple
Exemple
Reprenons $R=(\table 0.8,0.15,0.7,1.5;1,0.2,1,2;1.6,0.35,1.8,4.5)$.
On a alors, par exemple: $r_{11}=0,8$ $r_{23}=1$ $r_{32}=0,35$ $r_{34}=4,5$
Définitions
On appelle matrice nulle d'ordre $n$ la matrice carrée d'ordre $n$, notée souvent $O_n$, dont tous les coefficients sont nuls.
On appelle matrice identité d'ordre $n$ la matrice carrée d'ordre $n$, notée souvent $I_n$, constituée de 1 pour les éléments de sa diagonale principale et de 0 pour les autres.
 Exemple
Exemple
$O_2=(\table 0,0;0,0)$
$I_1=(\table 1)$ $I_2=(\table 1,0;0,1)$ $I_3=(\table 1,0,0;0,1,0;0,0,1)$ $I_4=(\table 1,0,0,0;0,1,0,0;0,0,1,0;0,0,0,1)$
Egalité de matrices
Deux matrices sont égales si et seulement si elles ont les mêmes coefficients.
Définition
Si A est une matrice d'ordre $(n;p)$, alors la matrice transposée de A, notée ${}^t A$, est la matrice obtenue en échangeant les lignes et les colonnes de A.
Ce concept, hors programme, est néanmoins parfois très pratique.
 Exemple
Exemple
Reprenons $P=(\table 1, 0.2,1, 2)$, $Q=(\table 0.35;6;0.6;0.06)$ et $R=(\table 0.8,0.15,0.7,1.5;1,0.2,1,2;1.6,0.35,1.8,4.5)$.
Déterminer leurs transposées.
Corrigé
On obtient: ${}^t P=(\table 1; 0.2;1; 2)$
${}^t Q=(\table 0.35,6,0.6,0.06)$
${}^t R=(\table 0.8,1,1.6;0.15,0.2,0.35;0.7,1,1.8;1.5,2,4.5)$
Définition
Une matrice est dite symétrique lorsqu'elle est égale à sa transposée.
 Exemple
Exemple
La matrice $S=(\table 7,0,2,4;0,9,3,1;2,3,8,5;4,1,5,6)$ est symétrique.
b. Opérations
Produit d'une matrice par un réel
Soit $k$ un nombre réel et A une matrice.
Posons $C=kA$
La matrice $C$ est de même dimension que A, et chacun de ses coefficients $c_{ij}$ vérifie $c_{ij}=k× a_{ij}$.
En particulier, on note: $-1A=-A$, et la matrice obtenue s'appelle la matrice opposée de A.
 Exemple
Exemple
Reprenons $R=(\table 0.8,0.15,0.7,1.5;1,0.2,1,2;1.6,0.35,1.8,4.5)$.
L'opposée de R est: $-R=(\table -0.8,-0.15,-0.7,-1.5;-1,-0.2,-1,-2;-1.6,-0.35,-1.8,-4.5)$.
Et on a, par exemple: $2R=(\table 1.6,0.30,1.4,3;2,0.4,2,4;3.2,0.70,3.6,9)$
Somme de matrices
Soit A et B deux matrices de même dimension.
Posons $C=A+B$
La matrice $C$ est de même dimension que A et B, et chacun de ses coefficients $c_{ij}$ vérifie $c_{ij}=a_{ij}+b_{ij}$.
 Exemple
Exemple
Soit $A=(\table 3,1;4,-1;-0.5,√{2})$ et $B=(\table0,-1;2,5;1,1)$ et $C=(\table0,-1;2,5)$
Déterminer, si possible $A+B$ et $A+C$.
On pose $C=3A-B$. Déterminer sans calculatrice la valeur de $c_{31}$
Corrigé
A et B ont même ordre; on peut les sommer.
On obtient, à la calculatrice (ou de tête): $A+B=(\table 3,0;6,4;0.5,1+√{2})$
A et C n'ont pas le même ordre; on ne peut pas les sommer.
Comme $C=3A-B$, on a: $c_{31}=3a_{31}-b_{31}=3 ×(-0,5)-1=-2,5$
Produit de matrices
Soient $n$, $p$ et $q$ trois entiers naturels non nuls.
Soit A une matrice de dimension $n×p$ et B une matrice de dimension $p×q$.
Posons $C=A×B$.
La matrice $C$ est de dimension $n×q$, et chacun de ses coefficients $c_{ij}$ vérifie $c_{ij}=a_{i1}×b_{1j}+a_{i2}×b_{2j}+...+a_{ip}×b_{pj}$
Attention! En général, la matrice $A×B$ n'existe que si le nombre de colonnes de A est égal au nombre de lignes de B.
Et, en cas d'existence, les matrices $A×B$ et $B×A$ sont souvent différentes. On dit que le produit matriciel n'est pas commutatif.
 Exemple
Exemple
Soit $A=(\table 1,-2,5;-3,4,-2)$ et $B=(\table4;-5;2)$
On pose $C=A×B$ et $D=B×A$
Déterminer, si possible, $C$ et $D$.
Retrouver sans calculatrice les valeur de $c_{11}$ et $c_{21}$.
Corrigé
A est de dimension $2×3$ et B est de dimension $3×1$.
A a 3 colonnes et B a 3 lignes. Donc $C=A×B$ existe.
$C$ sera de dimension $2×1$.
On obtient, à la calculatrice: $C=(\table 24;-36)$
B a 1 colonne et A a 2 lignes. Donc $D=B×A$ n'existe pas.
On a: $c_{11}=a_{11}×b_{11}+a_{12}×b_{21}+a_{13}×b_{31}=1×4+(-2)×(-5)+5×2=24$
Et: $c_{21}=a_{21}×b_{11}+a_{22}×b_{21}+a_{23}×b_{31}=-3×4+4×(-5)+(-2)×2=-36$
 Exemple
Exemple
Soit $A=(\table 1,2;3,4)$ et $B=(\table5,6;7,8)$ et $I=(\table1,0;0,1)$
On pose $C=A×B$ et $D=B×A$
Déterminer, sans calculatrice, $C$.
Déterminer, avec calculatrice, $D$.
Les matrices $C$ et $D$ sont-elles égales?
Déterminer les matrices $I×A$ et $A×I$.
Corrigé
A est de dimension $2×2$ et B est de dimension $2×2$.
A a 2 colonnes et B a 2 lignes. Donc $C=A×B$ existe.
$C$ sera de dimension $2×2$.
Pour effectuer le produit A×B à la main, on utilise souvent la présentation suivante, où A est en bas à gauche, et B en haut à droite.

Chaque coefficient du produit se trouve alors à l'intersection de la ligne de A et la colonne de B utiles à son calcul.
On a: $c_{11}=a_{11}×b_{11}+a_{12}×b_{21}=1×5+2×7=19$
Et: $c_{12}=a_{11}×b_{21}+a_{12}×b_{22}=1×6+2×8=22$
Et: $c_{21}=a_{21}×b_{11}+a_{22}×b_{12}=3×5+4×7=43$
Et: $c_{21}=a_{21}×b_{21}+a_{22}×b_{22}=3×6+4×8=50$
On obtient donc: $C=(\table 19,22;43,50)$
On obtient, à la calculatrice: $D=(\table 23,34;31,46)$
On constate que C et D sont différentes.
On obtient facilement: $I×A=A×I=A$
Propriété
Soit $I_n$ la matrice identité d'ordre $n$.
Pour toute matrice carrée A d'ordre $n$, on a:
$I_n×A=A×I_n=A$
Propriété
Pour toutes matrices A, B et C ayant des dimensions "convenables", on a:
$A×(B+C)=A×B+A×C$
$(B+C)×A=B×A+C×A$
$A×(B×C)=(A×B)×C$ (les parenthèses sont donc ici inutiles)
Puissance de matrice
Soit $p$ un entier naturel non nul.
Si A est un matrice carrée d'ordre $n$, alors $A^p$ est la matrice carrée d'ordre $n$, définie par l'égalité:
$A^p=A×A×...×A$ (A apparait p fois)
Par convention: $A^0=I_n$
 Exemple
Exemple
$A=(\table -1,-2;-5,3)$
On obtient (à la calculatrice): $A^2=(\table 11,-4;-10,19)$
et $A^3=(\table 9,-34;-85,77)$
c. Inverses
Définition
Si A est un matrice carrée d'ordre $n$, alors $A$ est inversible si et seulement si il existe
une matrice carrée B d'ordre $n$ telle que $A×B=B×A=I_n$
Dans ce cas, la matrice B s'appelle la matrice inverse de A et on note $B=A^{-1}$
Propriété
Si A et B sont deux matrices de même ordre $n$, et si $A×B=I_n$,
alors: $B×A=I_n$, et par là: $B=A^{-1}$
 Exemple
Exemple
$A=(\table -1,-2;-5,3)$ et $B=(\table 6,3;14,7)$
et $C=(\table 1,2;3,4)$ et $D=(\table -2,1;a,b)$
Déterminer, à la calculatrice, les inverses de A et B, si elles existent.
On admet que C est inversible et que $D=C^{-1}$. Déterminer $a$ et $b$
Corrigé
On obtient, à la calculatrice: $A^{-1}=(\table -{3}/{13},-{2}/{13};-{5}/{13},{1}/{13})$
On constate, à la calculatrice, que B n'est pas inversible.
$D=C^{-1}$ Donc on a $C×D=I_2$
Or: $C=(\table 1,2;3,4)$ $D=(\table -2,1;a,b)$ $I_2=(\table 1,0;0,1)$
Donc: $C×D=I_2$ $⇔$ $\{\table 1×(-2)+2×a=1, 1×1+2×b=0;3×(-2)+4×a=0, 3×1+4×b=1$
$⇔$ $\{\table a={3}/{2}, b=-{1}/{2};a={6}/{4}, b=-{2}/{4}$
$⇔$ $a={3}/{2}$ et $b=-{1}/{2}$
On constate donc que $D=(\table -2,1;{3}/{2},-{1}/{2})$
On peut le vérifier à la calculatrice.
Savoir faire
Chacun doit être capable de rentrer une matrice dans sa calculatrice, d'en afficher un coefficient particulier, d'effectuer toutes les opérations avec les matrices, de déterminer l'inverse d'une matrice.
A la demande de certains, je développe ici le cas des matrices d'ordre 2.
Définition
Soit $A=(\table a,b;c,d)$ une matrice carrée d'ordre $2$.
Le déterminant de $A$, noté $det(A)$, est le nombre réel défini par:
$det(A)=ad-bc$
Propriété
Une matrice carrée $A$ d'ordre 2 est inversible si et seulement si $det(A)≠0$.
Si $A=(\table a,b;c,d)$ et si $A$ est inversible, alors $A^{-1}={1}/{det(A)}(\table d,-b;-c,a)$
$A$ est une matrice carrée d'ordre $2$.
On calcule: $det(A)=1×4-3×2=-2$
Comme $det(A)≠0$, la matrice $A$ est inversible,
et on obtient: $A^{-1}={1}/{-2}(\table 4,-2;-3,1)$
Soit: $A^{-1}=(\table -2,1;1.5,1-0.5)$
d. Exemples de représentations matricielles
 Exemple de transformation géométrique du plan
Exemple de transformation géométrique du plan
Le plan est muni d'un repère orthonormé (O,I,J).
Les coordonnées d'un point ou d'un vecteur peuvent alors s'écrire sous forme:
d'un couple $(x;y)$, ou d'une matrice ligne $(\table x,y)$, ou d'une matrice colonne $(\table x;y)$.
Ici, nous adopterons l'écriture en matrice colonne.
On considère la transformation du plan, notée $s$, telle que:
l'image de tout point $M(\table x;y)$ par $s$ est un point $M'(\table x';y')$ défini par $(\table x';y')=A×(\table x;y)$,
où $A$ est la matrice d'ordre 2 définie par: $A=(\table -{3}/{5},{4}/{5};{4}/{5},{3}/{5})$.
Déterminer les images des points $O(\table 0;0)$, $A(\table 1;0)$, $B(\table 1;1)$ et $C(\table 3;1)$.
Placer tous les points sur un graphique, sur lequel on aura tracé la droite $d$ d'équation $y=2x$.
Conjecturer la nature de la transformation $s$.
A la calculatrice (ou de tête), on obtient: $0'(\table 0;0)$ $A'(\table -0.6;0.8)$ $B'(\table 0.2;1.4)$
$C'(\table -1,3)$
Voici un graphique convenable.
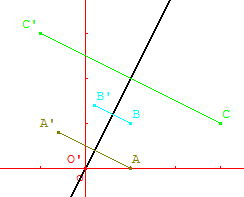
On conjecture que la transformation $s$ est la symétrie axiale par rapport à la droite $d$ (tracée en noir sur le graphique).
Résolution de systèmes linéaires à $n$ équations et $n$ inconnues
Tout système de ce type peut s'écrire sous la forme $A×X=B$, où A est la matrice carrée d'ordre $n$ des coefficients du système, X est la matrice colonne des $n$ inconnues, et B est une matrice colonne de $n$ réels.
Si A est inversible, alors le système admet une solution unique X donnée par $X=A^{-1}×B$
 Exemple
Exemple
On considère le système (S) $\{\table -x+2y=3;x-7y=2$
(S) $⇔$ $A×X=B$ avec
$A=(\table -1,2;1,-7)$ $X=(\table x;y)$ et $B=(\table 3;2)$
A l'aide de la calculatrice, on constate que A est inversible et que $A^{-1}=(\table -{7}/{5},-{2}/{5};-{1}/{5},-{1}/{5})$.
En multipliant à gauche chaque membre de l'égalité par $A^{-1}$, on obtient:
(S) $⇔$ $A^{-1}×A×X=A^{-1}×B$ $⇔$ $I_2×X=A^{-1}×B$ (cette ligne et la précédente sont facultatives)
On a donc: (S) $⇔$ $X=A^{-1}×B$
A l'aide de la calculatrice, on obtient alors: (S) $⇔$ $X=(\table -5;-1)$
 Exemple
Exemple
Résoudre, si possible, le système (S) $\{\table x+y+z=125;2x+3y+z=136;x+2y+3z=143$
Corrigé
(S) $⇔$ $A×X=B$ avec
$A=(\table 1,1,1;2,3,1;1,2,3)$ $X=(\table x;y;z)$ et $B=(\table 125;136;143)$
A l'aide de la calculatrice, on constate que A est inversible et que $A^{-1}=(\table {7}/{3},-{1}/{3},-{2}/{3};-{5}/{3},{2}/{3},{1}/{3};{1}/{3},-{1}/{3},{1}/{3})$.
On a donc: (S) $⇔$ $X=A^{-1}×B$
A l'aide de la calculatrice, on obtient alors: (S) $⇔$ $X=(\table 151;-70;44)$
Définition
Soit $(U_n)$ une suite de matrices colonnes à $p$ lignes.
La suite $(U_n)$ est définie par son premier terme (en général la matrice colonne $U_0$),
et par la relation de récurrence $U_{n+1}=A×U_n+C$, où A est une matrice carrée d'ordre $p$, et C une matrice colonne à $p$ lignes.
Dans ce cas, l'état stable, s'il existe, est la matrice colonne à $p$ lignes S qui vérifie $S=A×S+C$
Définition
Soit $(U_n)$ une suite de matrices colonnes à $p$ lignes. Et soit L une matrice colonne à $p$ lignes.
La suite $(U_n)$ tend vers L lorsque la limite quand $n$ tend vers $+∞$ de chaque coefficient de $U_n$ est égale au coefficient de L correspondant.
Méthode
Soit $(U_n)$ une suite de matrices colonnes vérifiant la relation de récurrence $U_{n+1}=A×U_n+C$.
On peut facilement démontrer que:
Si la suite $(U_n)$ tend vers une matrice L, alors L est nécessairement l'état stable.
Si la suite $(U_n)$ admet un état stable S, alors la suite $(V_n)$ vérifiant $V_n=U_n-S$ est telle que $V_{n+1}=AV_n$, ce qui implique que $V_n=A^n×V_0$, ce qui permet d'obtenir une formule explicite pour $U_n$.
 Exemple
Exemple
Soit $(a_n)$ et $(b_n)$ deux suites définies par:
$a_0=10$, $b_0=20$, $a_{n+1}=0,9a_n-0,7b_n+4$ et $b_{n+1}=0,2b_n+3$
On pose $U_n=(\table a_n;b_n)$
La suite $(U_n)$ est définie par son premier terme $U_0=(\table 10;20)$,
et par la relation de récurrence $U_{n+1}=A×U_n+C$.
- Donner les matrices A et C.
- Déterminer, s'il existe, l'état stable S.
- On considère la suite $(V_n)$ vérifiant $V_n=U_n-S$.
Montrer que $V_{n+1}=AV_n$. - Montrer par récurrence que $V_n=A^n×V_0$.
- Montrer par récurrence que $A^n=(\table 0.9^n,0.2^n-0.9^n;0,0.2^n)$.
-
Déterminer une formule explicite pour $U_n$ en fonction de $A^n$ et $U_0$ et S.
Puis en déduire que: $a_n=-20×0,9^n+16,25×0,2^n+13,75$
et: $b_n=16,25×0,2^n+3,75$ - Montrer que, si la suite $(U_n)$ tend vers une matrice L, alors $L=S$.
- Montrer que la suite $(U_n)$ tend vers effectivement vers S.
Corrigé
- On a: $\{\table a_{n+1}=0.9a_n-0.7b_n+4; b_{n+1}=0a_n+0.2b_n+3$
Or: $U_{n+1}=A×U_n+C$
Donc: $A=(\table 0.9,-0.7;0,0.2)$ et $C=(\table 4;3 )$. - $S=A×S+C$ $⇔$ $I_2×S-A×S=C$ $⇔$ $(I_2-A)×S=C$
Or: $I_2-A=(\table 0.1,0.7; 0,0.8)$
A la calculatrice, on obtient: $(I_2-A)^{-1}=(\table 10,-8.75;0,1.25)$
Ce qui permet d'écrire: $S=(I_2-A)^{-1}×C$
Et, à la calculatrice, on obtient alors: $S=(\table 13.75;3.75)$
L'état stable existe et vaut $S=(\table 13.75;3.75)$ - On considère la suite $(V_n)$ vérifiant: $V_n=U_n-S$.
Donc: $V_{n+1}=U_{n+1}-S$.
Soit: $V_{n+1}=A×U_n+C-S$.
Or, comme $S=A×S+C$, on a: $S-A×S=C$
On obtient donc: $V_{n+1}=A×U_n+S-A×S-S$.
Soit: $V_{n+1}=A×U_n-A×S=A×(U_n-S)$.
Soit: $V_{n+1}=A×V_n$. - Pour tout entier naturel $n$, notons $ P_n $ la propriété : $V_n=A^n×V_0$.
Montrons par récurrence que, pour tout entier naturel $n$, $ P_n $ est vraie.
Initialisation : On a: $ A^0×V_0=I_2×V_0=V_0$ , donc $ P_0 $ est vraie.
Hérédité : Soit $n$ un entier naturel, supposons que $P_n$ soit vraie.
On a donc: $V_n=A^n×V_0$.
Or: $V_{n+1}=A×V_n$.
D'où: $V_{n+1}=A×A^n×V_0$.
Soit: $V_{n+1}=A^{n+1}×V_0$.
Et par là: $ P_{n+1} $ est vraie.
Conclusion: pour tout naturel $n$, $V_n=A^n×V_0$ - Pour tout entier naturel $n$, notons $ Q_n $ la propriété : $A^n=(\table 0.9^n,0.2^n-0.9^n;0,0.2^n)$.
Montrons par récurrence que, pour tout entier naturel $n$, $ Q_n $ est vraie.
Initialisation : On a: $ (\table 0.9^0,0.2^0-0.9^0;0,0.2^0)=(\table 1,0;0,1)=I_2=A^0$ , donc $ Q_0 $ est vraie.
Hérédité : Soit $n$ un entier naturel, supposons que $Q_n$ soit vraie.
On a donc: $A^n=(\table 0.9^n,0.2^n-0.9^n;0,0.2^n)$.
Or: $A^{n+1}=A×A^n$.
Nous calculons à la main les quatres coefficients du produit $A×A^n$.
On rappelle que $A=(\table 0.9,-0.7;0,0.2)$ et $A^n=(\table 0.9^n,0.2^n-0.9^n;0,0.2^n)$
On obtient les quatres coefficients:
$\{\table0.9×0.9^n-0.7×0\,\,\,\,\,,0.9×(0.2^n-0.9^n)-0.7×0.2^n;0×0.9^n+0.2×0\,\,\,\,\,,0×(0.2^n-0.9^n)+0.2×0.2^n$
Soit: : $\{\table0.9^{n+1}\,\,\,\,\,,0.9×0.2^n-0.9^{n+1}-0.7×0.2^n;0\,\,\,\,\,,0.2^{n+1}$
Soit: : $\{\table0.9^{n+1}\,\,\,\,\,,0.2×0.2^n-0.9^{n+1};0\,\,\,\,\,,0.2^{n+1}$
Soit: : $\{\table0.9^{n+1}\,\,\,\,\,,0.2^{n+1}-0.9^{n+1};0\,\,\,\,\,,0.2^{n+1}$
On reconnait les quatres coefficients prévus pour $A^{n+1}$
Et par là: $ Q_{n+1} $ est vraie.
Conclusion: pour tout naturel $n$, $A^n=(\table 0.9^n,0.2^n-0.9^n;0,0.2^n)$. - Comme $V_n=A^n×V_0$ et $V_n=U_n-S$, on obtient:
$U_n=A^n×V_0+S$
Soit: $U_n=A^n×(U_0-S)+S$
C'est la formule explicite demandée.
On a donc: $(\table a_n;b_n)=(\table 0.9^n,0.2^n-0.9^n;0,0.2^n)×(\table -3.75;16.25)+(\table 13.75;3.75)$
Soit: $(\table a_n;b_n)=(\table 0.9^n×(-3.75)+(0.2^n-0.9^n)×16.25;0.2^n×16.25)+(\table 13.75;3.75)$
Soit: $(\table a_n;b_n)=(\table -20×0.9^n+16.25×0.2^n+13.75;16.25×0.2^n+3.75)$
Donc on a bien: $a_n=-20×0,9^n+16,25×0,2^n+13,75$
et: $b_n=16,25×0,2^n+3,75$ - Si $\lim↙{n→+∞}(U_n)=L$, alors, par passage à la limite dans l'égalité $U_{n+1}=A×U_n+C$, on obtient: $L=A×L+C$, ce qui prouve que $L=S$.
- Si $q$ est dans $[0;1[$, alors on a: $\lim↙{n→+∞}(q^n)=0$
Donc: $\lim↙{n→+∞}(a_n)=-20×0+16,25×0+13,75=13,75$
et $\lim↙{n→+∞}(b_n)=16,25×0+3,75=3,75$
Donc la suite $(U_n)$ tend vers la matrice $(\table13.75;3.75)$
Il s'agit évidemment de l'état stable.
II Les graphes
a. Les graphes non orientés
Définitions
Un graphe non orienté est un ensemble fini de "sommets" reliés (ou non) par une (ou des) "arête(s)".
Deux sommets reliés par une arête sont dits adjacents.
Un sommet non relié à d'autres est dit isolé .
Une arête reliant un sommet à lui même s'appelle une boucle.
L'ordre d'un graphe est le nombre de ses sommets.
Le degré d'un sommet est le nombre d'arêtes issues de ce sommet, les boucles étant comptées deux fois.
Un sous-graphe $G'$ d'un graphe $G$ est un graphe comprenant certains sommets de $G$ ainsi que certaines des arêtes reliant ces sommets.
Un graphe est simple si le graphe ne possède pas de boucle, et si deux sommets quelconques sont reliés par au plus une arête.
 Exemple
Exemple
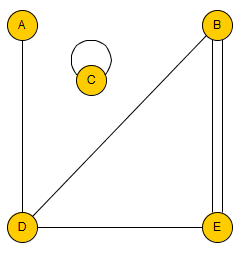
Le graphe ci-dessus est d'ordre 5. Le sommet C est isolé. Deux arêtes relient B à E.
A a pour degré 1. B a pour degré 3. C a pour degré 2.
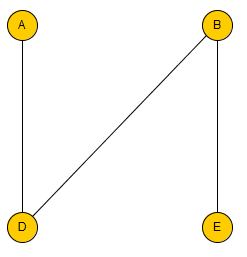
Le graphe ci-dessus est un sous-graphe du précédent.
Le sommet C a été supprimé. Un arête reliant B à E et l'arête reliant D à E ont été supprimées.
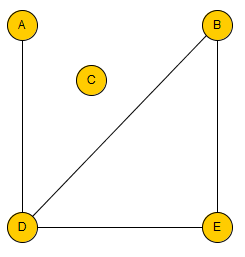
Le graphe ci-dessus est simple. Il est d'ordre 5. Le sommet C est isolé.
A a pour degré 1. B a pour degré 2. C a pour degré 0.
Propriété
Dans un graphe non orienté simple, la somme des degrés des sommets est égale au double du nombre d'arêtes.
Et par là, cette somme est paire.
 Exemple
Exemple
Reprenons le dernier graphe de l'exemple précédent.

Voici le tableau donnant les degrés des sommets.

La somme des degrés vaut 8. Le graphe a donc 4 arêtes.
Ici, le nombre d'arêtes est évident, mais ce n'est pas toujours le cas...
 Exemple
Exemple
Comment organiser un tournoi entre 5 équipes de rugby de telle manière que chacune d'entre elles rencontre 3 équipes exactement?
Corrigé
Notons A, B, C, D et E les 5 équipes. Le problème revient à construire un graphe non orienté de sommets A, B, C, D et E. Les arêtes représenteraient les rencontres. Chaque sommet devrait être de degré 3.
Et, dans ce cas, la somme des degrés vaudrait 15. Cela est impossible car 15 n'est pas pair.
Donc un tel tournoi ne peut pas être organisé.
Définition
Un graphe non orienté est complet lorsque le graphe est simple et que tous ses sommets sont adjacents.
 Exemple
Exemple
Voici 3 graphes complets.
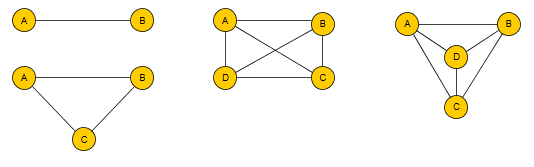
Les deux graphes de droite sont équivalents.
Définition
Dans un graphe non orienté, une chaîne est une suite d'arêtes consécutives. C'est aussi la suite des sommets correspondants.
La longueur d'une chaîne est égale à son nombre d'arêtes.
Une chaîne est fermée si son premier sommet est confondu avec son dernier sommet.
Un cycle est une chaîne fermée dont les arêtes sont distinctes deux à deux.
 Exemple
Exemple
Reprenons le dernier graphe de l'exemple précédent.

A-D-B est une chaîne de longueur 2.
E-B-D-A-D-E est une chaîne fermée de longueur 5.
E-B-D-E est un cycle de longueur 3.
Définition
Un graphe non orienté est connexe lorsque deux sommets quelconques mais distincts peuvent être reliés par une chaîne.
 Exemple
Exemple
Le graphe ci-dessous n'est pas connexe car, par exemple, on ne peut pas relier B et C par une chaîne.
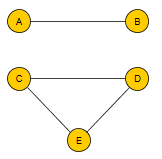
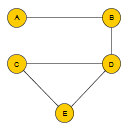
Le graphe ci-dessous est connexe car, comme il existe une chaîne qui passe par tous les sommets (par exemple la chaîne A-B-D-C-E ), deux sommets quelconques mais distincts sont forcément reliés par une chaîne.
Définition et propriété
Un chaîne eulérienne est une chaîne qui contient chaque arête du graphe une fois et une seule.
Théorème d'Euler
Considérons un graphe non orienté connexe. Ce graphe admet une chaîne eulérienne si et seulement si le nombre $n_{imp}$ de ses sommets de degré impair vaut 0 ou 2.
Et dans ce cas, si $n_{imp}=0$, alors la chaîne est un cycle, et si $n_{imp}=2$, alors la chaîne a pour extrémités les 2 sommets de degré impair.
 Exemple
Exemple

Ce graphe admet-il une chaîne eulérienne? Si oui, en donner une.
Corrigé
Ce graphe est connexe et a exactement 2 sommets de degré impair: A et D.
Donc il admet une chaîne eulérienne d'extrémités A et D.
Par exemple: A-B-D-E-C-D, A-B-D-C-E-D ou D-C-E-D-B-A sont de telles chaînes eulériennes.
En cas de difficulté pour trouver une telle chaîne, il suffit de procéder de la façon suivante.
On détermine une chaîne simple allant de A à D, par exemple: A-B-D. Les arêtes sont "marquées" sur le graphe pour ne pas les utiliser deux fois.
Puis on "greffe" sur la chaîne un cycle issu de l'un de ses sommets. Par exemple: D-E-C-D.
On obtient alors la chaîne: A-B-D-E-C-D. Les nouvelles arêtes sont "marquées" sur le graphe.
Dès que toutes les arêtes sont "marquées", la chaîne est convenable. C'est le cas ici.
b. Les graphes orientés
Définitions
Un graphe orienté est un ensemble fini de "sommets" reliés (ou non) par une (ou des) "arc(s)".
Ces arcs ne peuvent être "parcourus" que dans un sens.
Ls définitions et propriétés des graphes non orientés vues dans ce cours s'appliquent aux graphes orientés (sauf exceptions signalées ci-dessous).
Dans le cadre d'un graphe orienté:
les arêtes s'appellent des arcs
les chaînes s'appellent des chemins
le degré d'un sommet dénombre les arcs entrants et sortants associés à ce sommet (une boucle est donc comptée 2 fois)
le graphe orienté est complet lorsqu'il ne possède pas de boucle et que tous ses sommets sont reliés par exactement 2 arcs opposés
la notion de chemin eulérien est hors programme.
 Exemple
Exemple
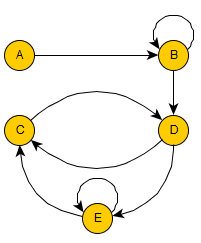
Le graphe ci-dessus est un graphe orienté d'ordre 5.
Définition
Considérons un graphe d'ordre $n$ dont on a ordonné les sommets et M une matrice carrée d'ordre $n$.
La matrice M est la matrice d'adjacence du graphe ordonné lorsque chaque coefficient $m_{ij}$ est égal au nombre d'arêtes (ou d'arcs) reliant les sommets de rangs $i$ et $j$.
Propriété
Toute matrice d'adjacence associée à un graphe non orienté est symétrique.
 Exemple
Exemple
Dans chacun des graphes qui suivent, les matrices d'adjacences supposent les sommets classés par ordre alphabétique.

Ce graphe admet pour matrice d'adjacence $M_1=(\table0,0,0,1,0;0,0,0,1,2;0,0,1,0,0;1,1,0,0,1;0,2,0,1,0)$

Ce graphe admet pour matrice d'adjacence $M_2=(\table0,0,1,0;0,0,1,1;1,1,0,0;0,1,0,0)$

Ce graphe admet pour matrice d'adjacence $M_3=(\table 0,1,0,0,0;0,1,0,1,0;0,0,0,1,0;0,0,1,0,1;0,0,1,0,1)$
Propriété
On considère un graphe ordonné de matrice d'adjacence M.
Soit $p$ un entier naturel non nul. On pose alors $A=M^p$.
Le nombre de chaînes (ou de chemins) reliant le sommet $i$ au sommet $j$ est donné par le coefficient $a_{ij}$.
 Exemple
Exemple

Déterminer le nombre de chemins de longueur 4 reliant B à E, reliant E à B.
Les citer tous.
Corrigé
Ce graphe admet pour matrice d'adjacence $M=(\table 0,1,0,0,0;0,1,0,1,0;0,0,0,1,0;0,0,1,0,1;0,0,1,0,1)$
A la calculatrice, on obtient: $M^4=(\table 0,1,2,2,2;0,1,4,3,4;0,0,2,1,2;0,0,3,2,3;0,0,3,2,3)$
Le coefficent situé ligne 2, colonne 5 vaut 4; par conséquent 4 chemins de longueur 4 relient B à E.
Il s'agit de: B-B-B-D-E B-B-D-E-E B-D-E-E-E B-D-C-D-E
Le coefficent situé ligne 5, colonne 2 vaut 0; par conséquent aucun chemin de longueur 4 ne relie E à B.
c. Les graphes pondérés et les graphes probabilistes
Définition
Un graphe est pondéré lorsque chacune de ses arêtes (ou chacun de ses arcs) est affecté d'un coefficient réel positif ou nul (appelé poids).
Un graphe probabiliste est un graphe orienté pondéré tel que, pour chaque sommet, la somme des poids des arcs sortants vaut 1.
Les poids sont alors nécessairement tous compris dans l'intervalle [0;1]; ils correspondent à des "probabilités".
Les sommets correspondent alors à des "états".
 Exemple
Exemple
On répète une expérience aléatoire à 2 issues A et B.
$A_n$: "l'état A est réalisé au bout de $n$ étapes.
$B_n$: "l'état B est réalisé au bout de $n$ étapes.
Si l'issue A s'est produite lors d'une étape, alors la probabilité qu'elle se produise à l'étape suivant vaut 0,75.
Si l'issue B s'est produite lors d'une étape, alors la probabilité qu'elle se produise à l'étape suivant vaut 0,20.
ona donc: $p_{A_n}(A_{n+1})=0,75$ et $p_{B_n}(B_{n+1})=0,20$
On peut alors dresser l'arbre de probabilités suivant.
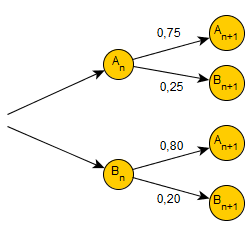
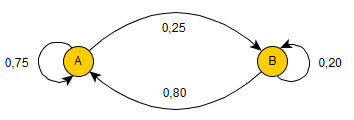
Cet arbre correspond alors au graphe probabiliste suivant.
Définition
Considérons un graphe probabiliste d'ordre $n$ dont on a ordonné les sommets et M une matrice carrée d'ordre $n$.
La matrice M est la matrice de transition du graphe probabiliste lorsque chaque coefficient $m_{ij}$ est égal au poids de l'arc reliant le sommet $i$ au sommet $j$ s'il existe, est égal à 0 sinon.
Propriété
Pour toute matrice de transition associée à un graphe probabiliste la somme des coefficients de chaque ligne vaut 1.
 Exemple
Exemple
Considérons le graphe probabiliste de l'exemple précédent.

Les sommets sont triés par ordre alphabétique.
La matrice de transition du graphe probabiliste est alors $M=(\table 0.75,0.25;0.8,0.20)$
d. Les chaînes de Markov
Définition
Une variable aléatoire $X$ sur l'univers $Ω$ d'une expérience aléatoire est une application de $Ω$ sur un ensemble E.
Définition
On considère une suite $(X_n)$ de variables aléatoires sur l'univers $Ω$ d'une expérience aléatoire, à valeurs dans un ensemble E fini représentant des "états".
Cette suite permet de modéliser l'évolution par étapes successives d'un système aléatoire possédant un nombre fini d'états.
La suite $(X_n)$ définit une chaîne de Markov lorsque, à chaque étape $n$ , les probabilités de transition d'un état à un autre ne dépendent pas de $n$.
La loi de probabilité de $X_0$ s'appelle la distribution initiale. Pour chaque étape $n$ (à partir de 1), la loi de probabilité de $X_n$ s'appelle la distribution après $n$ transitions.
Propriété
Une chaîne de Markov peut être associée à un graphe probabiliste dont les sommets représentent les états du système aléatoire, et dont les poids sont les probabilités de transition entre 2 états.
La même chaîne de Markov peut être associée à la matrice de transition de ce graphe probabiliste.
 Exemple
Exemple
Une mouche volète dans un appartement de 3 pièces A, B et C qui communiquent entre elles.
Parfois elle s'approche d'une ouverture entre 2 pièces.
Si elle est dans la pièce A, alors:
la probabilité qu'elle reste dans la pièce A vaut 0,7,
la probabilité qu'elle passe dans la pièce B vaut 0,1,
la probabilité qu'elle passe dans la pièce C vaut 0,2,
Si elle est dans la pièce B, alors:
la probabilité qu'elle passe dans la pièce A vaut 0,6,
la probabilité qu'elle reste dans la pièce B vaut 0,3,
la probabilité qu'elle passe dans la pièce C vaut 0,1,
Si elle est dans la pièce C, alors:
la probabilité qu'elle passe dans la pièce A vaut 0,4,
la probabilité qu'elle passe dans la pièce B vaut 0,2,
la probabilité qu'elle reste dans la pièce C vaut 0,4,
On note $X_n$ la position de la mouche à la n-ième approche d'une ouverture.
Au début de l'expérience, la mouche est en B.
- La suite $(X_n)$ définit une chaîne de Markov. Pourqoui?
- Donner la distribution initiale du système.
- Donner un arbre pondéré associé aux 2 premières transitions, et déterminer la distribution après ces 2 transitions.
- Donner le graphe probabiliste et la matrice de transition qui sont associés à la chaîne de markov(les sommets étant pris dans l'odre alphabétique).
Corrigé
- La suite $(X_n)$ définit une chaîne de Markov car, à chaque étape $n$ , les probabilités de transition d'un état à un autre ne dépendent pas de $n$.
- Au début de l'expérience, la mouche est en B.
La distribution initiale du système est la suivante:
$p(X_0=A)=0$ $p(X_0=B)=1$ $p(X_0=C)=0$ - Voici un arbre pondéré associé aux 2 premières transitions.
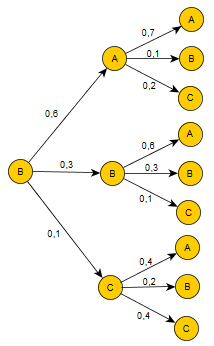
Déterminons la distribution après ces 2 transitions.
$\{A, B, C\}$ constitue une partition de l'univers. D'après la formule des probabilités totales, on obtient:
$p(X_2=A)=0,6×0,7+0,3×0,6+0,1×0,4=0,64$
$p(X_2=B)=0,6×0,1+0,3×0,3+0,1×0,2=0,17$
$p(X_2=C)=0,6×0,2+0,3×0,1+0,1×0,4=0,19$
-
Voici le graphe probabiliste et la matrice de transition demandés.
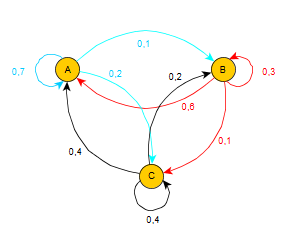
$P=(\table 0.7,0.1,0.2;0.6,0.3,0.1;0.4,0.2,0.4)$
Définition
On considère une chaîne de Markov $(X_n)$ à 2 états (numérotés 1 et 2) ou 3 états (numérotés 1,2 et 3)
La matrice de la distribution après $n$ transitions est la matrice ligne (à 2 ou 3 colonnes) $π_n$ qui vérifie:
$π_n=(\table p(X_n=1)\,\,\, p(X_n=2))$ pour 2 états
$π_n=(\table p(X_n=1)\,\,\, p(X_n=2) \,\,\, p(X_n=3))$ pour 3 états
Si $n=0$, il s'agit de la matrice de la distribution initiale.
Propriété
On considère une chaîne de Markov $(X_n)$, sa matrice de transition P, et sa matrice de la distribution après $n$ transitions $π_n$.
Pour tout entier naturel $n$, on a:
$π_{n+1}=π_n×P$ et $π_{n}=π_0×P^n$
 Exemple
Exemple
On reprend l'exemple précédent.
Donner la matrice de la distribution initiale $π_0$.
Retrouver la distribution après 2 transitions par un calcul matriciel.
Corrigé
La distribution initiale du système est la suivante:
$p(X_0=A)=0$ $p(X_0=B)=1$ $p(X_0=C)=0$
Donc: $π_0=(\table 0,1,0)$
On sait que: $π_{2}=π_0×P^2$
Or: $P=(\table 0.7,0.1,0.2;0.6,0.3,0.1;0.4,0.2,0.4)$
Donc on obtient (à la calculatrice): $π_2=(\table 0.64,0.17,0.19)$
On retrouve le fait que:
$p(X_2=A)=0,64$
$p(X_2=B)=0,17$
$p(X_2=C)=0,19$
Propriété
On considère une chaîne de Markov $(X_n)$, sa matrice de transition P, et sa matrice de la distribution après $n$ transitions $π_n$.
S'il existe un entier $k$ tel que $P^k$ ne comporte pas de coefficient nul, alors la suite $(π_n)$ converge vers une matrice de distribution $π$, unique solution de l'équation $π=π×P$.
Une telle matrice $π$ est dite "distribution invariante" du système.
Cette matrice $π$ est indépendante de la distribution initiale $π_0$.
 Exemple
Exemple
On reprend encore l'exemple précédent.
Déterminer la distribution invariante du système et interpréter le résultat.
Corrigé
On a: $P=(\table 0.7,0.1,0.2;0.6,0.3,0.1;0.4,0.2,0.4)$
On constate tout d'abord que la matrice de transition $P$ ne comporte pas de zéro.
Donc la suite $(π_n)$ converge vers une matrice de distribution $π$, unique solution de l'équation $π=π×P$.
Résolvons l'équation $π=π×P$.
On pose: $π=(\table a, b, c)$ avec $a+b+c=1$ (un détail à ne pas oublier!)
Par conséquent: $π=(\table a, b, 1-a-b)$
Donc: $π=π×P$ $ ⇔$ $\{\table a=a×0.7+b×0.6+(1-a-b)×0.4;b=a×0.1+b×0.3+(1-a-b)×0.2;1-a-b=a×0.2+b×0.1+(1-a-b)×0.4$
Soit: $π=π×P$ $ ⇔$ $\{\table a=0.7a+0.6b+0.4-0.4a-0.4b;b=0.1a+0.3b+0.2-0.2a-0.2b;1-a-b=0.2a+0.1b+0.4-0.4a-0.4b$
Soit: $π=π×P$ $ ⇔$ $\{\table a-0.7a+0.4a-0.6b+0.4b=0.4;-0.1a+0.2a-0.3b+0.2b+b=0.2;-a-0.2a+0.4a-b-0.1b+0.4b=0.4-1$
Soit: $π=π×P$ $ ⇔$ $\{\table 0.7a-0.2b=0.4;0.1a+0.9b=0.2;-0.8a-0.7b=-0.6$
On considère les 2 premières lignes du système; on obtient le système (S) $\{\table 0.7a-0.2b=0.4;0.1a+0.9b=0.2$
(S) $⇔$ $A×X=B$ avec
$A=(\table 0.7,-0.2;0.1,0.9)$ $X=(\table a;b)$ et $B=(\table0.4;0.2)$
A l'aide de la calculatrice, on constate que A est inversible et que $A^{-1}=(\table {18}/{13},{4}/{13};-{2}/{13},{14}/{13})$.
On a donc: (S) $⇔$ $X=A^{-1}×B$
A l'aide de la calculatrice, on obtient alors: (S) $⇔$ $X=(\table a;b)=(\table {8}/{13};{2}/{13})$
Notons que $-0.8×{8}/{13}-0.7×{2}/{13}=-0.6$. La 3ème ligne du système est donc vraie pour ces valeurs de $a$ et $b$. Cela était assuré car, d'après la propriété ci-dessus, l'équation $π=π×P$ a une solution.
On calcule alors $c=1-a-b={3}/{13}$.
La solution unique de l'équation $π=π×P$ est $π=(\table {8}/{13},{2}/{13},{3}/{13})$, qui est la distribution invariante du système.
La suite $(π_n)$ converge alors vers $π$, ce qui signifie que, lorsque $n$ tend vers $+\∞$, la probabilité que la mouche soit dans la pièce A tend vers ${8}/{13}$,
la probabilité que la mouche soit dans la pièce B tend vers ${2}/{13}$, et la probabilité que la mouche soit dans la pièce C tend vers ${3}/{13}$.