Dérivées, convexité
Dérivées, convexité
A SAVOIR: le cours sur Dérivées, convexité
Exercice 7
Soit $f$ définie sur $\ℝ$ par $f(x)=-x^3-1.5x^2+1,5$.
- Etudier la convexité de la fonction $f$ .
- Déterminer le point d'inflexion A de $\C_f$.
- Montrer que la tangente $t$ à $\C_f$ au point A admet pour équation $y=0,75x+1,625$.
 Sans calcul, prouver que $f(0,6)≤0,75×0,6+1,625$.
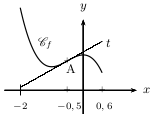
Sans calcul, prouver que $f(0,6)≤0,75×0,6+1,625$.- Tracer rapidement l'allure de $\C_f$ et de $t$ sur l'intervalle $[-2\,;\,0,6\,]$.
Placer A sur le dessin.
Corrigé
- $f\,'(x)=-3x^2-1,5×2x+0=-3x^2-3x$.
$f"(x)=-3×2x-3=-6x-3$.
$-6x-3$ est une fonction affine qui s'annule pour $x=-0,5$.
De plus, son coefficient directeur -6 est strictement négatif.
D'où le tableau de signes de $f\,''$ ci-contre.
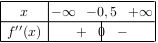
Par conséquent, $f$ est convexe sur $]-∞;-0,5]$ et concave sur $[-0,5;+∞[$.
- $f"$ s'annule en $-0,5$ en changeant de signe, par conséquent, $\C_f$ admet un point d'inflexion A en $-0,5$.
Comme $f(-0,5)=1,25$, le point d'inflexion A a pour coordonnées $(-0,5;1,25)$. - La tangente $t$ à $\C_f$ en $x_0$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
ici: $x_0=-0,5$, $f(x_0)=1,25$, $f\,'(x_0)=-3×(-0,5)^2-3×(-0,5)=0,75$.
D'où l'équation: $y=1,25+0,75(x-(-0,5))$.
Soit: $y=1,25+0,75x+0,375$.
Soit: $y=0,75x+1,625$. - On a vu que $f$ est concave sur $[-0,5;+∞[$. Donc elle y est en dessous de ses tangentes.
C'est vrai en particulier en $0,6$, et pour la tangente $t$ en $-0,5$.
Donc, pour $x=0,6$, l'ordonnée du point de $\C_f$ est inférieure à celle du point de $t$.
Et par là: $f(0,6)≤0,75×0,6+1,625$. -
Graphique ci-contre.