Fonction valeur absolue
Un conseil: revoir le cours sur la valeur absolue de la classe de seconde!
Définition
Soit $x$ un nombre réel. La valeur absolue de $x$, notée $|x|$, est la distance entre $x$ et $0$.
Ainsi, si si $x≤0$, alors $|x|=-x$, et si $x≥0$, alors $|x|=x$.
Exemple
$|4,2|=4,2$ $|-1,72|=1,72$ $|0|=0$
Propriété
Soit $r$ un nombre réel positif.
$|x|=r$ $⇔$ $x=r$ ou $x=-r$.
Exemple
Résoudre l'équation (1): $|3x+2|=10$
Corrigé
Dans cette équation, le domaine d'étude est $ℝ$.
(1) $⇔$ $|3x+2|=10$ $⇔$ $3x+2=10$ ou $3x+2=-10$
Soit: (1) $⇔$ $x={10-2}/{3}={8}/{3}$ ou $x={-10-2}/{3}=-4$
Donc $\S=\{-4; {8}/{3}\}$
Propriété
Pour tout $x$ réel, on a: $√{x^2}=$|$x$|
Exemple
En vous plaçant sur des intervalles convenables, écrire, en n'utilisant ni racine carrée, ni de valeur absolue, l'expression: $√{(x-2)^2}$
Corrigé
On a: $√{(x-2)^2}=$|$x-2$|.
On cherche le signe de $x-2$.
C'est une fonction affine, qui s'annule pour $x=2$. Comme son coefficient directeur $1$ est strictement positif, elle est strictement négative pour $x<2$, et
strictement positive pour $x>2$.
Donc: sur $]-\∞;2]$, on a: $√{(x-2)^2}=-(x-2)=-x+2$.
Sur $[2;+\∞[$, on a: $√{(x-2)^2}=x-2$.
Fonction valeur absolue
La fonction valeur absolue est la fonction $f$ dédinie, pour tout $x$ réel, par: $f(x)=|x|$.
En particulier, si $x≤0$, alors $f(x)=-x$, et si $x≥0$, alors $f(x)=x$.
La fonction valeur absolue est représentée par 2 demi-droites issues de l'origine.
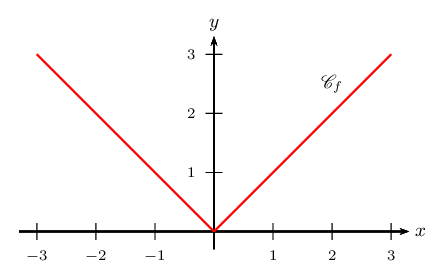
La fonction valeur absolue est dérivable partout, sauf en 0.
Si $x$<$0$, alors $f'(x)=-1$, et si $x$>$0$, alors $f'(x)=1$.
Exemple
Soit $f$ la fonction définie par $f(x)=|x|$.
En revenant à la définition, montrer que $f'(0)$ n'existe pas.
Corrigé
On rappelle que, s'il existe, alors: $f'(0)= \lim↙{h→0}r(h)$, où: $r(h)={f(0+h)-f(0)}/{h}$ pour $h$ non nul.
Or, pour $h$<$0$, on a: $r(h)={-(0+h)-0}/{h}={-0-h-0}/{h}={-h}/{h}=-1$.
Et par là: $\lim↙{h→0^-}r(h)=-1$.
De même, pour $h$>$0$, on a: $r(h)={(0+h)-0}/{h}={0+h-0}/{h}={h}/{h}=1$.
Et par là: $\lim↙{h→0^+}r(h)=1$.
Et comme une limite est unique, on en déduit que $\lim↙{h→0}r(h)$ n'existe pas, et par là, $f'(0)$ n'existe pas.