 Polynômes du second degré
Polynômes du second degré
Exercice 3
Déterminer le signe de $f$ sur l'intervalle I dans chacun des cas suivants:
L'étude du signe des polynômes du second degré de cet exercice sera justifiée par l'utilisation, si possible, de la forme factorisée de ces polynômes.
- $f(x)=-6x^2-x+1$ sur $\R$
- $f(x)=x^2-14x+49$ sur $I=[0;+∞[$
- $f(x)=-5x^2+x-3$ sur $I=\R$
- $f(x)=x^2-9$ sur $I=\R$
- $f(x)=-3x^2-14$ sur $I=\R$
- $f(x)={x^2+7}/{x^2-x-6}$ sur $I=[0;5]$
Corrigé
-
$f(x)=-6x^2-x+1$.
$f$ est un trinôme du second degré avec $a=-6$, $b=-1$ et $c=1$.
$Δ=b^2-4ac=(-1)^2-4×(-6)×1=25$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={1-5}/{-12}={1}/{3}$ et $x_2={-b+√Δ}/{2a}={1+5}/{-12}=-0,5$.
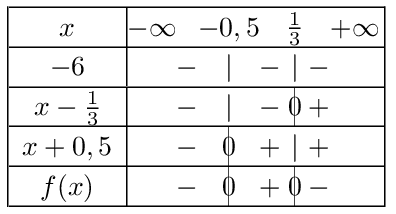
D'où l'écriture factorisée: $f(x)=-6(x-{1}/{3})(x+0,5)$
D'où le tableau suivant:
- $f(x)=x^2-14x+49$.
$f$ est un trinôme du second degré avec $a=1$, $b=-14$ et $c=49$.
$Δ=b^2-4ac=(-14)^2-4×1×49=0$.
$Δ=0$. Le trinôme a 1 racine double $x_0={-b}/{2a}={14}/{2}=7$.
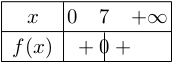
Donc $f(x)=1(x-7)^2=(x-7)^2$
Nous sommes en présence d'un carré. D'où le tableau suivant:
Autre méthode: $f(x)=x^2-2×x×7+7^2=(x-7)^2$
On retrouve le carré précédent, nul en 7, et strictement positif ailleurs! - $f(x)=-5x^2+x-3$.
$f$ est un trinôme du second degré avec $a=-5$, $b=1$ et $c=-3$.
$Δ=b^2-4ac=1^2-4×(-5)×(-3)=-59$.
$Δ<0$. Le trinôme n'a pas de racine.
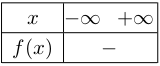
Son signe reste constant. On note alors que $f(0)=c=-3$ et que cette image est strictement négative. D'où le tableau suivant:
- $f(x)=x^2-9$
$f$ est un trinôme du second degré avec $a=1$, $b=0$ et $c=-9$.
La connaissance de la fonction carré nous insite à procéder de la façon suivante.
On sait que: $x^2-9=0$ $⇔$ $x^2=9$ $⇔$ $x=-3$ ou $x=3$.
Et: $x^2-9$>$0$ $⇔$ $x^2$>$9$ $⇔$ $x$<$-3$ ou $x$>$3$.
Et enfin: $x^2-9$<$0$ $⇔$ $x^2$<$9$ $⇔$ $-3$<$x$<$3$.
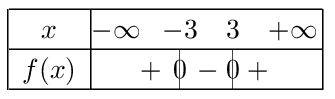
D'où le tableau suivant:
Pour ceux qui ont quelques lacunes sur la fonction carré,
revoir par exemple cet exercice de seconde. - $f(x)=-3x^2-14$
$f$ est un trinôme du second degré avec $a=-3$, $b=0$ et $c=-14$.
Comme $b=0$, et que $a$ et $c$ sont de mêmes signes, le signe du trinôme est évident.
$x^2≥0$, donc $-3x^2≤0$, et donc $-3x^2-14<-14$.
Donc: $∀x∈ℝ$, $f(x)$<$0$ - $f(x)={x^2+7}/{x^2-x-6}$ sur $I=[0;5]$
$f(x)$ est un quotient.
Le numérateur $x^2+7$ est un trinôme du second degré, qui est la somme d'un carré et de 7. Il reste donc strictement positif.
Par conséquent, le quotient sera du signe du dénominateur, ce qui nous autorise à ne pas faire apparaître le numérateur dans le tableau.
Le dénominateur $x^2-x-6$ est un trinôme du second degré avec $a=1$, $b=-1$ et $c=-6$.
$Δ=b^2-4ac=(-1)^2-4×1×(-6)=25$.
$Δ>0$. Le trinôme a 2 racines
$x_1={-b-√Δ}/{2a}={1-5}/{2}=-2$ (hors intervalle)
et $x_2={-b+√Δ}/{2a}={1+5}/{2}=3$.
D'où l'écriture factorisée: $x^2-x-6=(x+2)(x-3)$
Or, entre $0$ et $5$, $x+2$ reste strictement positif.
Donc le trinôme est du signe de $x-3$, qui est une fonction affine, nulle en 3, de coefficient directeur strictement positif.
D'où le tableau suivant:

On remarquera que, comme $3$ annule le dénominateur, c'est une valeur interdite!