Polynômes du second degré
Exercice 4
Dans cet exercice, l'étude du signe des polynômes du second degré sera justifiée par l'utilisation, si possible, de la forme factorisée de ces polynômes.
Résoudre l'inéquation sur l'intervalle I dans chacun des cas suivants:
- $-6x^2>x-1$ sur $\R$
- $-5x^2+x-3>0$ sur $I=\R$
-
$x^3≥9x$ sur $I=[-5;-1]$ - ${x^2+7}/{x^2-x-6}≥0$ sur $I=\ℝ$
Corrigé
- $\D_E=\ℝ$
$-6x^2>x-1$ $⇔$ $-6x^2-x+1>0$.
Le membre de gauche est un trinôme du second degré avec $a=-6$, $b=-1$ et $c=1$.
$Δ=b^2-4ac=(-1)^2-4×(-6)×1=25$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={1-5}/{-12}={1}/{3}$ et $x_2={-b+√Δ}/{2a}={1+5}/{-12}=-0,5$.
D'où l'écriture factorisée: $-6x^2-x+1=-6(x-{1}/{3})(x+0,5)$
D'où le tableau suivant:
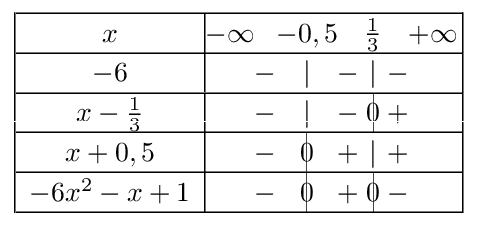
Donc S$=]-0,5;{1}/{3}[$ - $\D_E=\ℝ$
$-5x^2+x-3>0$.
Le membre de gauche est un trinôme du second degré avec $a=-5$, $b=1$ et $c=-3$.
$Δ=b^2-4ac=1^2-4×(-5)×(-3)=-59$.
$Δ<0$. Le trinôme n'a pas de racine.
Donc le trinôme reste toujours de signe constant.
Et comme l'image de 0 vaut $-3$, le trinôme reste strictement négatif.
Il n'est donc jamais positif. Donc S$=∅$ - $\D_E=\ℝ$
$x^3≥9x$ $⇔$ $x^3-9x≥0$ $⇔$ $x(x^2-9)≥0$
Le membre de gauche est un produit.
$x$ est une fonction linéaire, nulle en 0, strictement négative pour $x<0$, et strictement positive pour $x>0$.
En particulier, $x$<$0$ sur $I=[-5;-1]$.
$x^2-9$ est un trinôme du second degré avec $a=1$, $b=0$ et $c=-9$.
La connaissance de la fonction carré nous insite à procéder de la façon suivante.
On sait que: $x^2-9=0$ $⇔$ $x^2=9$ $⇔$ $x=-3$ ou $x=3$.
Et: $x^2-9$>$0$ $⇔$ $x^2$>$9$ $⇔$ $x$<$-3$ ou $x$>$3$.
Et enfin: $x^2-9$<$0$ $⇔$ $x^2$<$9$ $⇔$ $-3$<$x$<$3$.
On notera que la racine $-3$, hors intervalle, n'apparait pas dans le tableau.
Finalement, on a donc le tableau de signes suivant:
Donc S$=[-3;-1]$
Pour ceux qui ont quelques lacunes sur la fonction carré,
revoir par exemple cet exercice de seconde. - On veut résoudre l'inéquation ${x^2+7}/{x^2-x-6}≥0$
${x^2+7}/{x^2-x-6}$ est un quotient Q.
Le dénominateur $x^2-x-6$ est un trinôme du second degré avec $a=1$, $b=-1$ et $c=-6$.
$Δ=b^2-4ac=(-1)^2-4×1×(-6)=25$.
$Δ>0$. Le trinôme a 2 racines
$x_1={-b-√Δ}/{2a}={1-5}/{2}=-2$
et $x_2={-b+√Δ}/{2a}={1+5}/{2}=3$.
Donc $\D_E=\ℝ ∖\{-2;3\}$
Il y a donc 2 valeurs interdites!
Le numérateur $x^2+7$ est un trinôme, qui est la somme d'un carré et de 7. Il reste donc strictement positif.
Par conséquent, le quotient Q est du signe du dénominateur.
Le dénominateur $x^2-x-6$ est un trinôme de racines $-2$ et $3$.
D'où l'écriture factorisée: $x^2-x-6=(x+2)(x-3)$
D'où le tableau suivant:
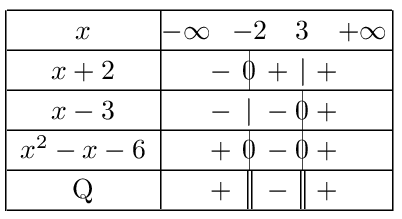
Donc S$=]-\∞;-2[∪]3;+\∞[$