 Variations
Variations
Exercice 2
Partie A
Nous allons déterminer ici un résultat de cours situé dans la partie 2 du chapitre sur les polynômes du second degré.
On considère un trinôme du second degré $p(x)=ax^2+bx+c$, avec $a$, $b$ et $c$ réels fixés, et $a$ non nul.
Déterminer $p\,'(x)$, puis le signe de $p\,'(x)$ sur $\R$, et dresser alors le tableau de variation de $p$ sur $\R$ .
Montrer que, si la forme canonique de $p(x)$ est $a(x-x_0)^2+y_0 $, alors $x_0={-b}/{2a}$ et $y_0=p(x_0)$.
Partie B
Ce qui suit est répétitif, mais indispensable...
Déterminer $f\,'$, puis le signe de $f\,'$ sur I, et dresser alors le tableau de variation de $f$ sur l'intervalle I dans chacun des cas suivants:
- $f(x)=√{x}+x^3+x$ sur $I=]0;+∞[$
- $f(x)=-5x^2+x+3$ sur $I=\R$
- $f(x)=8x^2-x+9$ sur $I=[0;{1}/{16}]$
- $f(x)=-x^3+{3}/{2}x^2$ sur $I=\R$
- $f(x)=-2x^3-0,5x^2+x+3$ sur $\R$
- $f(x)={x^2}/{2x+1}$ sur $I=[-1;-0,5[$
Partie C
A partir des tableaux de variation obtenus dans la partie B, en déduire, dans chacun des 6 cas, les extrema locaux de la fonction $f$. Préciser si l'on peut affirmer qu'il s'agit d'extrema absolus.
Partie D
$f$ est définie et dérivable sur [-2;3].
Si $f(0)$ est un extremum local de $f$, peut-on en déduire que $f'(0)=0$?
Si $f(0)$ est un maximum local de $f$, peut-on en déduire que $f(0)$ est le maximum de $f$?
Si $f'(0)=0$, peut-on en déduire que $f(0)$ est un extremum local de $f$?
Si $f(3)$ est un minimum local de $f$, peut-on en déduire que $f'(3)=0$?
Corrigé
Partie A
$p(x)=ax^2+bx+c$
$p\,'(x)=a×2x+b=2ax+b$.
$p\,'(x)$ est une fonction affine de coefficient directeur $2a$, et qui s'annule en $α={-b}/{2a}$.
Si $a$>$0$, alors $p$ admet le tableau de variations suivant:
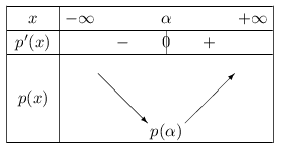
Si $a$<$0$, alors $p$ admet le tableau de variations suivant:
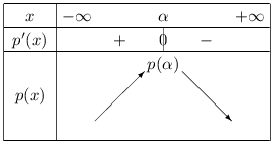
Supposons que la forme canonique de $p(x)$ soit $a(x-x_0)^2+y_0 $.
En développant, on obtient: $p(x)=a(x^2-2x_0x+x_0^2)+β=ax^2-2ax_0x+ax_0^2+β$.
En dérivant, on obtient: $p'(x)=2ax-2ax_0$.
C'est une fonction affine qui s'annule en $x_0$.
Donc, d'après ce qui précède, on obtient: $x_0=α={-b}/{2a}$.
Le fait que $y_0=β=p(α)=p(x_0)$ est une évidence.
Nous avons déterminé ici un résultat de cours situé dans la partie 2 du chapitre sur les polynômes du second degré.
Partie B
- $f(x)=√{x}+x^3+x$ sur $I=]0;+∞[$.
$f\,'(x)={1}/{2√{x}}+3x^2+1$.
$f\,'$ est une somme de termes.
Les termes ${1}/{2√{x}}$ et $3x^2$ sont positifs, le terme 1 est strictement positif.
Donc $f\,'$ est strictement positive sur $I=]0;+∞[$.
D'où le tableau de variation de $f$ sur I.
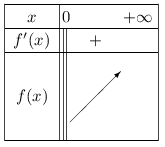
- $f(x)=-5x^2+x+3$ sur $I=\R$.
$f\,'(x)=-5×2x+1+0=-10x+1$.
$f\,'$ est une fonction affine de coefficient $-10$ strictement négatif.
On note que: $-10x+1=0⇔-10x=-1⇔x={-1}/{-10}=0,1$.
D'où le tableau de variation de $f$ sur I.
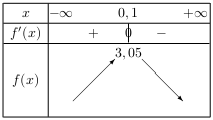
Ce tableau pouvait se trouver directement grâce au résultats de la partie A. En effet, $f$ est un trinôme avec $a=-5$ strictement négatif et $α={-b}/{2a}={-1}/{-10}=0,1$. - $f(x)=8x^2-x+9$ sur $I=[0;{1}/{16}]$.
$f\,'(x)=8×2x-1+0=16x-1$.
$f\,'$ est une fonction affine de coefficient $16$ strictement positif.
On note que: $16x-1=0⇔16x=1⇔x={1}/{16}$.
D'où le tableau de variation de $f$ sur I.
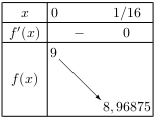
Ce tableau pouvait se trouver directement grâce au résultats de la partie A. En effet, $f$ est un trinôme avec $a=8$ strictement positif et $α={-b}/{2a}={1}/{16}$. - $f(x)=-x^3+{3}/{2}x^2$ sur $I=\R$.
$f\,'(x)=-3x^2+{3}/{2}2x=-3x^2+3x=-3x(x-1)$.
$f\,'$ est un produit de 2 facteurs, chacun d'eux étant une fonction affine (voire linéaire pour le premier).
$-3x$ a pour coefficient $-3$ strictement négatif.
$x-1$ a pour coefficient $1$ strictement positif.
On note que: $-3x=0⇔x={0}/{-3}=0$.
On note que: $x-1=0⇔x=1$.
D'où le tableau de variation de $f$ sur I.
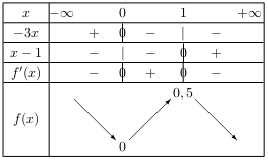
-
$f(x)=-2x^3-0,5x^2+x+3$ sur $\R$.
$f\,'(x)=-2×3x^2-0,5×2x+1=-6x^2-x+1$.
$f\,'$ est un trinôme avec $a=-6$, $b=-1$ et $c=1$.
$Δ=b^2-4ac=(-1)^2-4×(-6)×1=25$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={1-5}/{-12}={1}/{3}$ et $x_2={-b+√Δ}/{2a}={1+5}/{-12}=-0,5$.
On factorise le trinôme: $f\,'(x)=-6(x-{1}/{3})(x+0,5)$ D'où le tableau suivant:
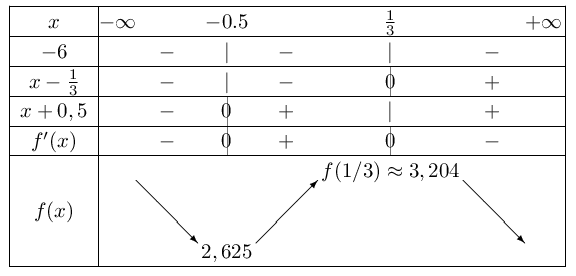
- $f(x)={x^2}/{2x+1}$ sur $I=[-1;-0,5[$.
On pose $f={u}/{v}$ avec $u=x^2$ et $v=2x+1$.
D'où $f\,'={u'v-uv'}/{v^2}$ avec $u'=2x$ et $v'=2$.
Soit $f\,'(x)={2x×(2x+1)-x^2×2}/{(2x+1)^2}={4x^2+2x-2x^2}/{(2x+1)^2}={2x^2+2x}/{(2x+1)^2}={2x(x+1)}/{(2x+1)^2}$.
Le numérateur est un produit de 2 facteurs, chacun d'eux étant une fonction affine (voire linéaire pour le premier).
$2x$ a pour coefficient $2$ strictement positif.
$x+1$ a pour coefficient $1$ strictement positif.
On note que: $2x=0⇔x={0}/{2}=0$.
On note que: $x+1=0⇔x=-1$.
Le dénominateur est un carré strictement positif pour $x≠-0,5$.
D'où le tableau de variation de $f$ sur I.

Partie C
- Tableau de variation de $f$

$f$ n'a pas d'extremum local, ni d'extremum absolu. - Tableau de variation de $f$

$f$ admet 3,05 pour maximum local. Il s'agit du maximum absolu de $f$. - Tableau de variation de $f$

$f$ admet 9 pour maximum local. Il s'agit du maximum absolu de $f$.
$f$ admet 8,96875 pour minimum local. Il s'agit du minimum absolu de $f$. - Tableau de variation de $f$

$f$ admet 0,5 pour maximum local. On ne sait pas s'il s'agit du maximum absolu de $f$.
$f$ admet 0 pour minimum local. On ne sait pas s'il s'agit du minimum absolu de $f$. - Tableau de variation de $f$

$f$ admet f(1/3) pour maximum local. On ne sait pas s'il s'agit du maximum absolu de $f$.
$f$ admet 2,625 pour minimum local. On ne sait pas s'il s'agit du minimum absolu de $f$. - Tableau de variation de $f$

$f$ admet -1 pour maximum local.Il s'agit du maximum absolu de $f$.
Partie D
$f$ est définie et dérivable sur [-2;3].
Si $f(0)$ est un extremum local de $f$, alors, comme 0 est à l'intérieur de [-2;3], on en déduit que $f'(0)=0$.
Si $f(0)$ est un maximum local de $f$, alors $f(0)$ n'est pas forcément le maximum de $f$.
Si $f'(0)=0$, alors $f(0)$ n'est pas forcément un extremum local de $f$. On sait seulement que la tangente en 0 est "horizontale".
Si $f(3)$ est un minimum local de $f$, alors, comme l'abscisse 3 est à l'extrémité de [-2;3], on n'a pas forcément $f'(3)=0$. La tangente n'est pas forcément "horizontale" à l'extrémité de la courbe représentative de $f$.