 Variations
Variations
Exercice 6
Soit $a$ , $b$ et $c$ trois réels fixés. Le réel $a$ est supposé non nul.
Soit $f$ la fonction définie sur $ ℝ$ par $f(x)=ax^2+bx+c$
La fonction $C$ est représentée par la courbe $\P$ dans un repère orthonormé (O,I,J).
Le début de l'exercice est une redite de la Partie A de l'exercice 2 .
- Quelle est la nature de $f$?
- a. Déterminer $f\,'(x)$.
b. On suppose que $a$>$0$.
Déterminer le signe de $f\,'$ sur $ ℝ$, et dresser alors le tableau de variation de $f$ sur $ ℝ$.
c. On suppose que $a$<$0$.
Déterminer le signe de $f\,'$ sur $ ℝ$, et dresser alors le tableau de variation de $f$ sur $ ℝ$. - En déduire, suivant le signe de $a$, la nature de l'extremum de $β$ de $f$. Pour quelle abscisse $α$ est-il atteint?
- On peut alors montrer que $f(x)=a(x-α)^2+ β$.
On admet que $\P$ est une parabole.
Montrer que, pour tout réel $h$, on a: $f(α-h)=f(α+h)$.
Que peut-on en déduire concernant la parabole $\P$?
Solution...
Corrigé
- $f(x)=ax^2+bx+c$ (avec $a$ non nul)
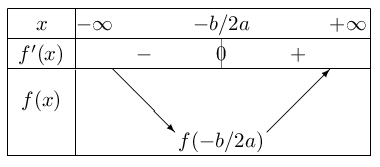
Donc $f$ est un trinôme du second degré. - a. $f\,'(x)=2ax+b$.
b. $2ax+b$ est une fonction affine, de coefficient directeur $2a$ strictement positif, qui s'annule pour $x={-b}/{2a}$.
D'où le tableau de variation de $f$ sur $ ℝ$.
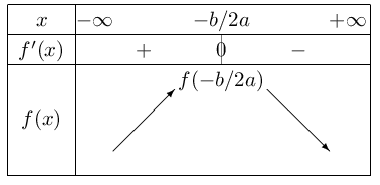
c. $2ax+b$ est une fonction affine, de coefficient directeur $2a$ strictement négatif, qui s'annule pour $x={-b}/{2a}$.
D'où le tableau de variation de $f$ sur $ ℝ$.
- Par conséquent:
Si $a$>$0$, alors $f$ admet un minimum.
Si $a$<$0$, alors $f$ admet un maximum.
Dans tous les cas, cet extremum est atteint pour l'abscisse $α={-b}/{2a}$ - On peut alors montrer que $f(x)=a(x-α)^2+ β$.
On admet que $\P$ est une parabole.
Soient $h$ un réel quelconque.
On a: $f(α-h)=a(α-h-α)^2+ β=a(-h)^2+β=ah^2+β$
Et on a: $f(α+h)=a(α+h-α)^2+ β=ah^2+β$
Donc: $f(α-h)=f(α+h)$, et c'est vrai pour tout réel $h$.
Donc, comme les axes du repère orthonormé sont perpendiculaires, la parabole $\P$ admet pour axe de symétrie la droite d'équation $x=α$.
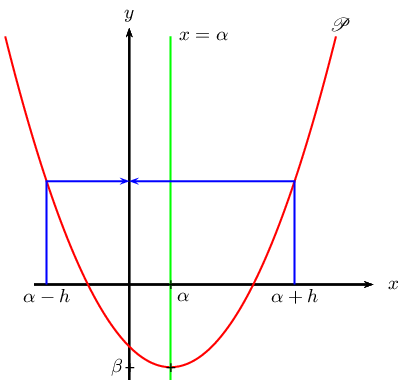
Le point de coordonnées $(α,β)$ s'appelle le "sommet" de la parabole $\P$.
Les personnes observatrices auront remarqué que, si $a$>$0$, alors le "sommet" est en bas!