 Les vecteurs
Les vecteurs
Exercice 2
Partie A
1. On suppose que ${u}↖{→}={t}↖{→}+{w}↖{→}$ et ${v}↖{→}=2,5.{t}↖{→}+2,5.{w}↖{→}$
Montrer que ${u}↖{→}$ et ${v}↖{→}$ sont colinéaires.
2. On suppose que ${AB}↖{→}-3{AC}↖{→}={0}↖{→}$
Que dire des points A, B et C?
3. On suppose que ${AE}↖{→}-2{EF}↖{→}={EF}↖{→}-{EB}↖{→}$
Que dire des droites (AB) et (EF)?
Partie B
Le plan est rapporté à un repère orthonormé (O,I,J).
On considère les points $T(1;2)$, $H(4;0)$ et $G(16;-8)$.
Montrer que ces 3 points sont alignés.
Partie C
Le plan est rapporté à un repère orthonormé (O,I,J).
On considère les points $A(1;2)$, $B(4;0)$, $C(6;3)$ et $D(x_D;y_D)$.
Répondre aux questions suivantes en utilisant des vecteurs.
Remarque: cette question peut aussi se traiter sans utiliser les vecteurs (voir l'exercice 1 sur la
géométrie analytique)
1. Soit $K(x_K;y_K)$ le milieu du segment [AC].
Déterminer les coordonnées du point K.
2. On suppose que le quadrilatère ABCD est un parallélogramme.
Déterminer les coordonnées du point D.
3. Faire une figure, puis conjecturer la nature du parallélogramme ABCD.
4. Prouver la conjecture proposée au 3.
Solution...
Corrigé
A savoir pour faire cet exercice:
les coordonnées du vecteur ${AB}↖{→}$ sont: $x_{{AB}↖{→}}=x_B-x_A$ et $y_{{AB}↖{→}}=y_B-y_A$.<
Partie A
1. On a: ${v}↖{→}=2,5.{t}↖{→}+2,5.{w}↖{→}=2,5.({t}↖{→}+{w}↖{→})=2,5.{u}↖{→}$
Donc ${u}↖{→}$ et ${v}↖{→}$ sont colinéaires.
2. On a: ${AB}↖{→}-3{AC}↖{→}={0}↖{→}$
Donc: ${AB}↖{→}=3{AC}↖{→}$
Donc les vecteurs ${AB}↖{→}$ et ${AC}↖{→}$ sont colinéaires.
Donc les points A, B et C sont alignés.
3. On a: ${AE}↖{→}-2{EF}↖{→}={EF}↖{→}-{EB}↖{→}$
Donc: ${AE}↖{→}+{EB}↖{→}={EF}↖{→}+2{EF}↖{→}$
Donc: ${AB}↖{→}={3{EF}↖{→}$ (d'après la relation de Chasles)
Donc les vecteurs ${AB}↖{→}$ et ${EF}↖{→}$ sont colinéaires.
Donc les droites (AB) et (EF) sont parallèles.
Partie B
On considère les points $T(1;2)$, $H(4;0)$ et $G(16;-8)$.
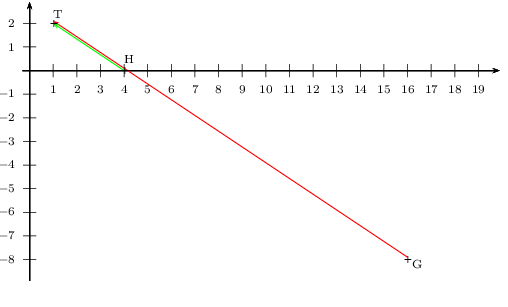
On a:: $x_{{HT}↖{→}}=x_T-x_H=1-4=-3$
et $y_{{HT}↖{→}}=y_T-y_H=2-0=2$
Donc: ${HT}↖{→}(-3;2)$
De même, on obtient: $x_{{GT}↖{→}}=x_T-x_G=1-16=-15$
et $y_{{GT}↖{→}}=y_T-y_G=2-(-8)=10$
Donc: ${GT}↖{→}(-15;10)$
On constate que: $x_{{GT}↖{→}}=5x_{{HT}↖{→}}$ et $y_{{GT}↖{→}}=5y_{{HT}↖{→}}$
Donc: ${GT}↖{→}=5{HT}↖{→}$
Donc les vecteurs ${GT}↖{→}$ et ${HT}↖{→}$ sont colinéaires.
Donc les points T, G et H sont alignés.
Partie C
1. K est le milieu de [AC], donc: ${AK}↖{→}={KC}↖{→}$
Donc: $x_K-x_A=x_C-x_K$ et $y_K-y_A=y_C-y_K$
Soit: $x_K-1=6-x_K$ et $y_K-2=3-y_K$
Donc: $x_K-1-6+x_K=0$ et $y_K-2-3+y_K=0$
Soit: $2x_K-7=0$ et $2y_K-5=0$
Donc: $x_K={7}/{2}=3,5$ et $y_K={5}/{2}=2,5$
Donc $K(3,5;2,5)$.
2. ABCD est un parallélogramme, donc: ${AB}↖{→}={DC}↖{→}$
Donc: $x_B-x_A=x_C-x_D$ et $y_B-y_A=y_C-y_D$
Soit: $4-1=6-x_D$ et $0-2=3-y_D$
Donc: $4-1-6+x_D=0$ et $0-2-3+y_D=0$
Soit: $-3+x_D=0$ et $-5+y_D=0$
Donc: $x_D=3$ et $y_D=5$
Donc $D(3;5)$.
3. Une figure convenable est tracée ci-dessous.
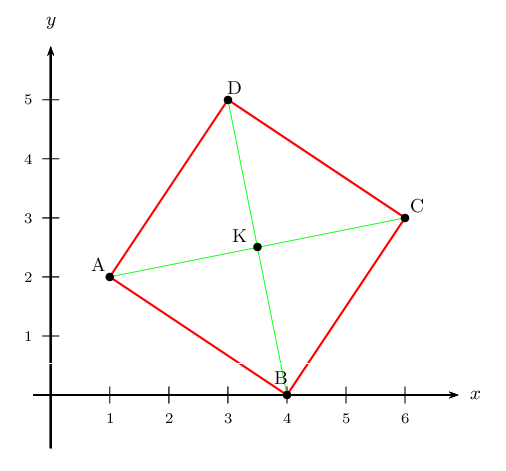
A savoir ici: une conjecture est une "propriété" qui n'a pas encore été démontrée.
Nous conjecturons que le parallélogramme ABCD est un carré.
4. La démonstration est donnée dans la réponse à la question 4. de l'exercice 1 sur les bases
de la géométrie analytique dans le plan.