 Limites de fonctions
Limites de fonctions
I Limites de référence
Limite infinie en $+∞$ ou en $-∞$
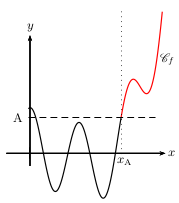
La fonction $f$ a pour limite $+∞$ en $+∞$ lorsque
toutes les images $f(x)$ deviennent aussi grandes que l'on veut pourvu que $x$ soit suffisamment grand.
On note $\lim↙{x→+∞}f(x)=+∞$.
Dans l'exemple graphique, pour n'importe quel nombre A (même s'il est très grand), toutes les images sont supérieures à A dès que $x$ dépasse une certaine valeur appelée $x_A$.
La fonction $f$ a pour limite $-∞$ en $+∞$ lorsque
toutes les images $f(x)$ deviennent aussi "négatives" que l'on veut pourvu que $x$ soit suffisamment grand.
On note $\lim↙{x→+∞}f(x)=-∞$.
La fonction $f$ a pour limite $+∞$ en $-∞$ lorsque
toutes les images $f(x)$ deviennent aussi grandes que l'on veut pourvu que $x$ soit suffisamment "négatif".
On note $\lim↙{x→-∞}f(x)=+∞$.
La fonction $f$ a pour limite $-∞$ en $-∞$ lorsque
toutes les images $f(x)$ deviennent aussi "négatives" que l'on veut pourvu que $x$ soit suffisamment "négatif".
On note $\lim↙{x→-∞}f(x)=-∞$.
Limites de référence
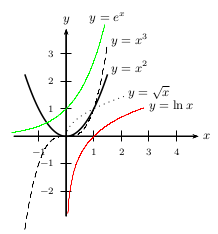
$\lim↙{x→+∞}x=+∞$ $\lim↙{x→+∞}x^2=+∞$ $\lim↙{x→+∞}x^3=+∞$ $\lim↙{x→+∞}√{x}=+∞$
$\lim↙{x→-∞}x=-∞$ $\lim↙{x→-∞}x^2=+∞$ $\lim↙{x→-∞}x^3=-∞$
$\lim↙{x→+∞}e^x=+∞$
Fonction vue en terminale
$\lim↙{x→+∞}\ln x=+∞$
Limite finie en $+∞$ ou en $-∞$
La fonction $f$ a pour limite $l$ en $+∞$ lorsque
toutes les images $f(x)$ deviennent aussi proches de $l$ que l'on veut pourvu que $x$ soit suffisamment grand.
On note $\lim↙{x→+∞}f(x)=l$.
On dit que, dans un repère, la droite $d$ d'équation $y=l$ est asymptote horizontale en $+∞$ à la courbe représentative $\C$ de $f$.
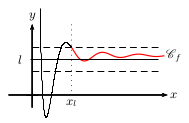
Dans l'exemple graphique, pour n'importe quelle bande horizontale centrée sur $l$ (même si elle est très fine), toutes les images sont dans cette bande dès que $x$ dépasse une certaine valeur appelée $x_l$.
La fonction $f$ a pour limite $l$ en $-∞$ lorsque
toutes les images $f(x)$ deviennent aussi proches de $l$ que l'on veut pourvu que $x$ soit suffisamment "négatif".
On note $\lim↙{x→-∞}f(x)=l$.
On dit que, dans un repère, la droite $d$ d'équation $y=l$ est asymptote horizontale en $-∞$ à la courbe représentative $\C$ de $f$.
Unicité
La limite d'une fonction est unique.
Fonction constante
Soit $l$ un nombre réel; si $f(x)=l$, alors $\lim↙{x→+∞}f(x)=\lim↙{x→-∞}f(x)=l$.
Limites de référence
$\lim↙{x→+∞}{1}/{x}=\lim↙{x→-∞}{1}/{x}=0$
$\lim↙{x→-∞}e^x=0$

Limite infinie en un nombre réel $a$
La fonction $f$ a pour limite $+∞$ en $a$ lorsque
toutes les images $f(x)$ deviennent aussi grandes que l'on veut pourvu que $x$ soit suffisamment proche de $a$.
On note $\lim↙{x→a}f(x)=+∞$.
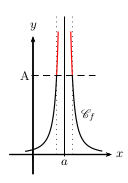
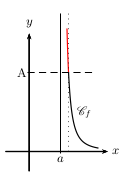
La fonction $f$ a pour limite $+∞$ à droite en $a$ lorsque
toutes les images $f(x)$ deviennent aussi grandes que l'on veut pourvu que $x$ soit suffisamment proche de $a$ tout en restant supérieur à $a$.
On note $\lim↙{{}^{x→a}_{x\text">"a}}f(x)=+∞$.
La fonction $f$ a pour limite $+∞$ à gauche en $a$ lorsque
toutes les images $f(x)$ deviennent aussi grandes que l'on veut pourvu que $x$ soit suffisamment proche de $a$ en restant inférieur à $a$.
On note $\lim↙{{}^{x→a}_{x\text"<"a}}f(x)=+∞$.
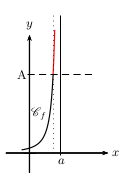
On définit de façon analogue une limite $-∞$ en $a$, à droite en $a$, ou à gauche en $a$.
Dans tous les cas précédents, on dit que, dans un repère, la droite $d$ d'équation $x=l$ est asymptote verticale en $a$ à la courbe représentative $\C$ de $f$.
Limites de référence
$\lim↙{{}^{x→0}_{x\text">"0}}{1}/{x}=+∞$ $\lim↙{{}^{x→0}_{x\text"<"0}}{1}/{x}=-∞$
Fonction vue en terminale
$\lim↙{x→0}\ln x=-∞$
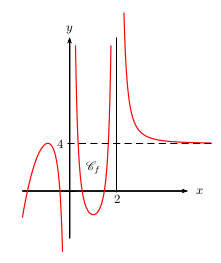
Exemple
Conjecturer la valeur de chacune des limites suivantes
$\lim↙{x→+∞}f(x)$
$\lim↙{x→-∞}f(x)$
$\lim↙{{}^{x→0}_{x\text"<"0}}f(x)$
$\lim↙{{}^{x→0}_{x\text">"0}}f(x)$
$\lim↙{x→2}f(x)$
Donner, s'il y a lieu, l'équation réduite de l'asymptote associée.
Corrigé
$\lim↙{x→+∞}f(x)=4$, donc la droite d'équation $y=4$ est asymptote horizontale en $+∞$ à $\C_f$.$\lim↙{x→-∞}f(x)=-∞$
$\lim↙{{}^{x→0}_{x\text"<"0}}f(x)=-∞$, donc la droite d'équation $x=0$ est asymptote verticale à $\C_f$.
$\lim↙{{}^{x→0}_{x\text">"0}}f(x)=+∞$, donc la droite d'équation $x=0$ est asymptote verticale à $\C_f$.
$\lim↙{x→2}f(x)=+∞$, donc la droite d'équation $x=2$ est asymptote verticale à $\C_f$.
Limite finie en un nombre réel $a$
La fonction $f$ a pour limite $l$ en $a$ lorsque
toutes les images $f(x)$ deviennent aussi proches de $l$ que l'on veut pourvu que $x$ assez "proche" de $a$.
On note $\lim↙{x→a}f(x)=l$.
Cette définition permet de définir d'une part la continuité,
d'autre part le nombre dérivé: $f\,'(a)=\lim↙{x→a}{f(x)-f(a)}/{x-a}=\lim↙{h→0}{f(a+h)-f(a)}/{h}$
Exemple
En appliquant la définition du nombre dérivé ci-dessus pour $a=0$ aux fonctions $e^x$ et $\ln(1+x)$, on obtient:
$\lim↙{x→0}{e^x-1}/{x}=1$ (car si $f(x)=e^x$, alors $f'(x)=e^x$, et en particulier, $f'(0)=e^0=1$)
Fonction vue en terminale
$\lim↙{x→0}{\ln (1+x)}/{x}=1$ (car si $f(x)=\ln (1+x)$, alors $f'(x)={1}/{1+x}$, et en particulier, $f'(0)=1$)
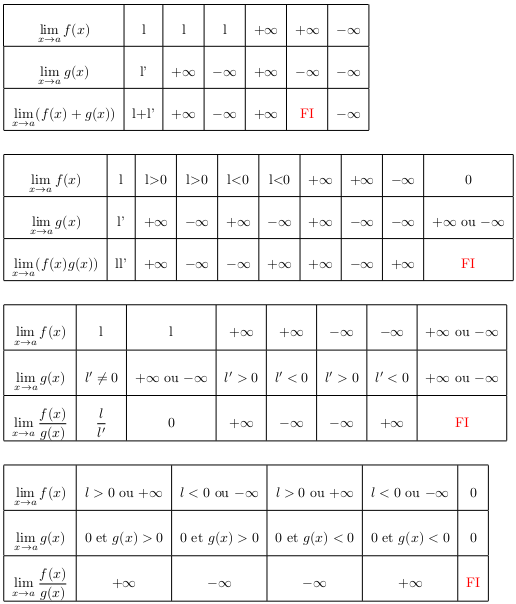
II Opérations et limites
Opérations
La détermination de la limite d'une somme, d'un produit ou d'un quotient de 2 fonctions est intuitive,
et vérifie les tableaux ci-dessous.
Dans ces tableaux, $a$ représente soit $+∞$, soit $-∞$, soit un nombre réel fixé.
Les méthodes utilisées pour déterminer les limites de suites se transposent aisément aux fonctions.
Si, dans un exercice, vous êtes confronté à une forme indéterminée (notée FI dans le tableau), alors vous serez guidés pour pouvoir déterminer la limite.
 Exemples
Exemples
- Soit $f$ la fonction définie par $f(x)=x^2(9-{1}/{x})+√{x}$ pour tout réel $x$.
Déterminer $\lim↙{x→+∞}f(x)$. - Soit $h$ la fonction définie par $h(x)=9\ln x-{1}/{x}$ pour tout réel $x$ non nul.
Déterminer $\lim↙{{}^{x→0}_{x\text">"0}}h(x)$.
Corrigé
- $f(x)=x^2(9-{1}/{x})+√{x}$
On a: $\lim↙{x→+∞}x^2=+∞$ et $\lim↙{x→+∞}9-{1}/{x}=9-0=9$.
Donc: $\lim↙{x→+∞}x^2(9-{1}/{x})=+∞$. (limite d'un produit)
Par ailleurs, on sait que: $\lim↙{x→+∞}√{x}=+∞$.
On obtient donc finalement: $\lim↙{x→+∞}f(x)=+∞$ (limite d'une somme). - $h(x)=9\ln x+(-{1}/{x})$.
On a: $\lim↙{{}^{x→0}_{x\text">"0}}\ln x=-∞$.
Et comme 9>0, on obtient: $\lim↙{{}^{x→0}_{x\text">"0}}9\ln x=-∞$.
Par ailleurs: comme $\lim↙{{}^{x→0}_{x\text">"0}}{1}/{x}=+∞$, on a: $\lim↙{{}^{x→0}_{x\text">"0}}-{1}/{x}=-∞$.
Donc finalement: $\lim↙{{}^{x→0}_{x\text">"0}}h(x)=-∞$ (limite d'une somme).
Avertissement
Les propriétés du III et du IV ne sont pas exigibles, et seront rappelées si besoin dans les exercices.
III Composées et limites
Composée
$a$, $b$ et $c$ désignent $+∞$, ou $-∞$, ou un nombre réel $a$.
Si $\lim↙{x→a}f(x)=b$ et si $\lim↙{y→b}g(y)=c$, alors $\lim↙{x→a}g(f(x))=c$
 Exemples
Exemples
Soit $h$ la fonction définie par $h(x)=√{x^2+{1}/{x}}$ pour tout réel $x$ non nul.
Déterminer $\lim↙{x→-∞}h(x)$.
Soit $m$ la fonction définie par $m(x)=e^{-3x+1}$ pour tout réel $x$.
Déterminer $\lim↙{x→+∞}m(x)$.
Corrigé
On a $h(x)=g(f(x))$ avec $f(x)=x^2+{1}/{x}$, et $g(y)=√{y}$.
Or, comme $\lim↙{x→-∞}x^2=+∞$ et $\lim↙{x→-∞}{1}/{x}=0$, on a $\lim↙{x→-∞}f(x)=+∞$.
De plus, $\lim↙{y→+∞}g(y)=+∞$.
Donc on obtient: $\lim↙{x→-∞}h(x)=+∞$.
$m(x)=e^{-3x+1}$
On a: $\lim↙{x→+∞}-3x+1=-∞$.
Or: $\lim↙{y→-∞}e^y=0$.
Donc: $\lim↙{x→+∞}m(x)=0$.
IV Comparaisons et limites
Théorème de comparaison
Si $\lim↙{x→+∞}f(x)=+∞$ et si, pour $x$ assez grand, $g(x)≥f(x)$,
alors $\lim↙{x→+∞}g(x)=+∞$.
Si $\lim↙{x→+∞}f(x)=-∞$ et si, pour $x$ assez grand, $g(x)≤f(x)$,
alors $\lim↙{x→+∞}g(x)=-∞$.
Ces deux propriétés s'étendent facilement pour des limites en $-∞$ ou en un réel $a$.
Théorème des gendarmes
Si $\lim↙{x→+∞}f(x)=l$ et si $\lim↙{x→+∞}h(x)=l$ et
si, pour $x$ assez grand, $f(x)≤g(x)≤h(x)$,
alors $\lim↙{x→+∞}g(x)=l$.
Cette propriété s'étend facilement pour des limites en $-∞$ ou en un réel $a$.
 Exemples
Exemples
- Soit $f$ la fonction définie par $f(x)=x^3-\cos x$ pour tout réel $x$.
Déterminer $\lim↙{x→+∞}f(x)$. - Soit $f$ la fonction définie par $f(x)=e^{x}\sin x$ pour tout réel $x$.
Déterminer $\lim↙{x→-∞}f(x)$.
Corrigé
- Pour tout réel $x$, on a: $-1≤\cos x≤1$, et par là: $-1+x^3≤\cos x+x^3≤1+x^3$.
En particulier: pour tout réel $x$, $-1+x^3≤f(x)$.
Or, comme $\lim↙{x→+∞}x^3=+∞$ et $\lim↙{x→+∞}-1=-1$, on obtient: $\lim↙{x→+∞}-1+x^3=+∞$.
Donc, par comparaison, on obtient $\lim↙{x→+∞}f(x)=+∞$. - Pour tout réel $x$, on a: $-1≤\sin x≤1$.
Et par là: $-1×e^{x}≤\sin x×e^{x}≤1×e^{x}$, soit: $-e^x≤f(x)≤e^x$.
Or, $\lim↙{x→-∞}e^x=0$ et $\lim↙{x→-∞}-e^x=0$.
Donc, d'après le "théorème des gendarmes", on obtient: $\lim↙{x→-∞}f(x)=0$.