Lois discrètes
A SAVOIR: le cours sur les Lois discrètes
Exercice 8
L'état veut tester certaines personnes pour déterminer si elles sont porteuses du virus C.
Il dispose d'un test produit par un institut réputé. Un test positif présume que le patient est porteur du virus C. Un test négatif présume que le patient n'est pas porteur du virus C.
La sensibilité $S_e$ du test est de $0,9$. Cela signifie que, si un patient porteur du virus C passe le test, alors la probabilité que le test soit positif vaut $0,9$.
La spécificité $S_p$ du test est de $0,98$. Cela signifie que, si un patient non porteur du virus C passe le test, alors la probabilité que le test soit négatif vaut $0,98$.
Ces 2 valeurs sont suffisantes pour que le test soit conforme aux recommandations de la Haute Autorité Sanitaire.
Par ailleurs, la prévalence du virus C vaut $p$. Cela signifie que la proportion de porteurs du virus C dans la population est $p$.
On teste une personne pris au hasard.
Soit M : " le patient est porteur du virus C ";
P : " le test est positif " ;
N : " le test est négatif ".
-
Représenter la situation par un arbre de probabilité.
Montrer que $p(P)=0,88p+0,02$ - La valeur prédictive positive du test, notée VPP, est la probabilité que la personne soit malade sachant que le test est positif.
Montrer que $ VPP ={90p}/{88p+2}$. - La valeur prédictive négative du test, notée VPN, est la probabilité que la personne ne soit pas malade sachant que le test est négatif.
Déterminer l'expression de $ VPP $ en fonction de $p$. - On pose $f(p)={90p}/{88p+2}$. Cette fonction est définie pour $p$ dans l'intervalle [0;1].
Déterminer la dérivée de $f$, puis dresser le tableau de variation de $f$ sur [0;1].
- On admet que la VPP et la VPN admettent les courbes représentatives ci-dessous.
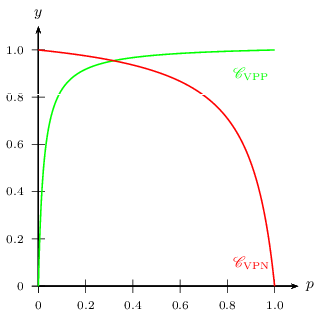
Remarquer que la courbe représentant la VPP est conforme au tableau de variation de $f$.
Que dire des évolutions respectives des Valeurs Prédictives? - Une personne passe le test en début d'épidémie. On a alors $p=1%$. Le test est positif. La personne doit-il nécessairement s'inquiéter?
Même question pendant le pic de l'épidémie où $p$ vaut $30%$.
Solution...
Corrigé
-
Voici un arbre de probabilité convenable.
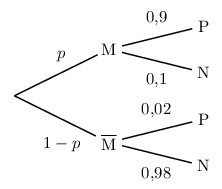
$\{M;M↖{−}\}$ constitue une partition de l'univers.
La probabilité cherchée est alors: $p(P)=p(M∩P)+p(M↖{−} ∩P)$ (par application de la formule des probabilités totales).
Soit: $p(P)=p(M)×p_M(P)+p(M↖{−})×p_{M↖{−}}(P)$ .
Soit: $p(P)=p×0,90+(1-p)×0,02=0,90p+0,02-0,02p$
Soit: $p(P)=0,88p+0,02$. c.q.f.d. - VPP est la probabilité que la personne soit malade sachant que le test est positif.
Donc: $ VPP= p_P(M)={p(M∩P)}/{p(P)}={p(M)×p_M(P)}/{p(P)}={p×0,90}/{0,88p+0,02}$ (on multiplie numérateur et dénominateur par 100)
Donc: $ VPP={90p}/{88p+2}$. c.q.f.d. - VPN est la probabilité que la personnet ne soit pas malade sachant que le test est négatif.
Donc: $ VPN= p_N(M↖{−})={p(M↖{−}∩N)}/{p(N)}={p(M↖{−})×p_{M↖{−}}(N)}/{1-p(P)}={(1-p)×0,98}/{1-0,88p-0,02}={0,98-0,98p}/{0,98-0,88p}$ (on multiplie numérateur et dénominateur par $-100$)
Donc: $ VPN={98p-98}/{88p-98}$. - On a: $f(p)={90p}/{88p+2}$ définie pour $p$ dans l'intervalle [0;1].
On pose: $f={u}/{v}$ avec $u=90p$ et $v=88p+2$.
D'où: $f'={u'v-uv'}/{v^2}$ avec $u'=90$ et $v'=88$.
Donc: $f'(p)={90(88p+2)-90p×88}/{(88p+2)^2}={7\,920p+180-7\,920p}/{(88p+2)^2}={180}/{(88p+2)^2}$
Le dénominateur est un carré, nul en $p=-{2}/{88}$ (hors intervalle), et strictement positif ailleurs.
Le numérateur 180 est strictement positif.
Par conséquent, $f'$ est strictement positive.
Et par là, $f$ est strictement croissante.
On calcule rapidement $f(0)=0$ et $f(1)=1$, et on obtient finalement le tableau de variation suivant.
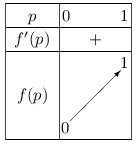
- La courbe représentant la VPP est bien conforme au tableau de variation de $f$.
On constate que la VPP croît rapidement de 0 à 1. Elle est faible quand la prévalence est faible car la proportion importante de personnes saines génère de nombreux "faux positifs".
La VPN décroît de 1 à 0. Elle diminue quand la prévalence diminue car la proportion importante de personnes infectées génère de nombreux "faux négatifs".
- Une personne passe le test en début d'épidémie. On a alors $p=1%$. Le test est positif.
On calcule la VPP.
$ VPP= p_P(M)={90×0,01}/{88×0,01+2}≈0,31$.
La personne a moins d'une chance sur trois d'être malade. Elle doit relativiser son inquiétude, surtout si aucun symptôme ne vient étayer ce résultat...
Une personne passe le test pendant le pic de l'épidémie. On a alors $p=30%$. Le test est positif.
On calcule la VPP.
$ VPP= p_P(M)={90×0,30}/{88×0,30+2}≈0,95$.
La personne risque fort d'être malade. Elle doit effectivement s'inquiéter, surtout si d'autres symptômes viennent étayer ce résultat...