 Lois discrètes
Lois discrètes
Un conseil: revoir le cours sur les probabilités conditionnelles et le cours sur les variables aléatoires de la classe de première!
I Loi discrète uniforme
Définition et propriété
Soit $n$ un entier naturel non nul, et soit $E=\{\, 1\, , \,2\, ,\, 3\, ,..., \,n\,\}$ les $n$ entiers de 1 à $n$.
La loi uniforme sur E est la loi de la variable aléatoire X telle que $X( Ω)=E$ et telle que, pour tout $k$ dans E, $p(X=k)={1}/{n}$
Propriété
Soit $n$ un entier naturel non nul, et soit $E=\{\, 1\, , \,2\, ,\, 3\, ,..., \,n\,\}$ les $n$ entiers de 1 à $n$.
La variable aléatoire X suivant la loi uniforme sur E admet pour espérance $E(X)={1+n}/{2}$
Exemple
On jette un dé.
Soit X la variable aléatoire donnant le résultat obtenu. Donner sa loi. Que vaut son espérance? Interpréter le résultat obtenu.
X suit la loi uniforme sur $E=\{\, 1\, , \,2\, ,\, 3\, ,..., \,6\,\}$.
On a:$X( Ω)=E$. Et, pour tout $k$ dans E, $p(X=k)={1}/{6}$
$E(X)={1+6}/{2}=3,5$
La valeur moyenne de X sur un très grand nombre de lancers tend vers 3,5.
II Loi de Bernoulli et loi binomiale
a. Succession d'épreuves indépendantes
Définition et propriété
$n$ épreuves successives sont indépendantes lorsque le résultat de l'une n'influe pas sur le résultat de l'autre.
Une succession de $n$ épreuves indépendantes est telle que, pour toute liste $(A_1, A_2,...,A_n)$ d'événements concernant les $n$ épreuves successives, on a:
$p(A_1∩A_2∩...∩A_n)=p(A_1)×p(A_2)×...×p(A_n)$
Une telle succession peut se représenter par un arbre de probabilité.
Exemple
On jette un dé, puis on tire un jeton d'un sac contenant les jetons R, V , B et J, puis on jette une pièce.
Soit G: "le résultat du dé vaut au moins 5"
Soit R: "le jeton est R"
Soit F: "la pièce est tombée sur Face"
Soit P: "la pièce est tombée sur Pile"
Modéliser l'expérience.
Nous sommes en présence de 3 épreuves indépendantes.
On a: $p(G)={2}/{6}={1}/{3}$ et $p(R)={1}/{4}$ et $p(F)={1}/{2}$
Représentation par un arbre de probabilité.
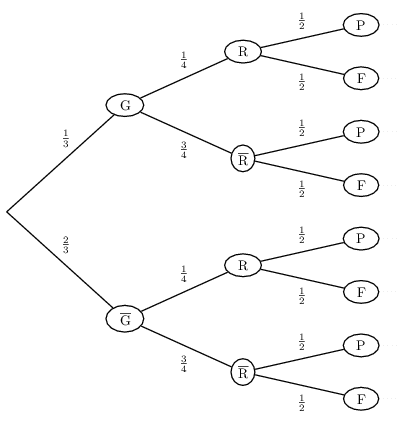
On a alors, par exemple: $p(G∩R∩F)=p(G)×p(R)×p(F)={1}/{3}×{1}/{4}×{1}/{2}={1}/{24}$
b. Loi de Bernoulli
Définition
Une épreuve de Bernoulli de paramètre $p$ est une expérience ayant 2 issues, appelées "succés" et "échec" telle que la probabilité de "succés" vaut $p$.
La loi de Bernoulli est la loi de la variable aléatoire X qui code le résultat d'une épreuve de Bernoulli de paramètre $p$ de la façon suivante:
$p(X=1)=p(« succès »)=p$ $p(X=0)=p(« échec »)=1-p$
Exemple
On lance une pièce. Soit X la variable aléatoire qui vaut 1 si on a obtenu Pile, et 0 si on a obtenu Face.
Si on appelle succès l'obtention de Pile, et échec l'obtention de Face, alors nous sommes en présence d'une épreuve de Bernoulli, et X suit la loi de Bernoulli.
On a ici: $p(X=1)=p(\text"obtenir Pile")=0,5$ $p(X=0)=p(\text"obtenir Face")=1-0,5=0,5$
c. Loi binomiale
Définitions
Un schéma de Bernoulli de paramètres n et p est l'expérience constituant à répéter $n$ fois de manière indépendante une épreuve de Bernoulli de paramètre $p$.
La loi de probabilité de la variable aléatoire X égale au nombre de succès au cours de ces $n$ épreuves
est appelée loi binomiale de paramètres n et p.
On note: $X=B (n,p)$.
Un schéma de Bernoulli se représente à l'aide d'un arbre pondéré
où les noeuds ont chacun 2 branches
et où les mêmes probabilités $p$ et $1-p$ sont répétées sur les couples de branches.
Exemple
Une usine fabrique des composants électriques.
On prélève au hasard 3 composants dans la production de la journée.
On suppose que les prélèvements sont indépendants l'un de l'autre,
et que la probabilité qu'un composant soit conforme au cahier des charges est égale à 0,84.
- Représenter l'expérience par un arbre pondéré.
- Enumérer tous les cas possibles dans un produit cartésien..
-
Soit X la variable aléatoire donnant le nombre de composants conformes parmi les 3.
Que dire de X? - Quelle est la probabilité que le premier composant soit conforme, mais pas les 2 suivants?
- Quelle est la probabilité que le second composant soit conforme, mais pas les 2 autres?
Corrigé
- arbre pondéré:
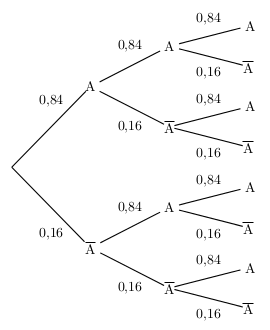
- Les 8 issues possibles sont: $\{(A,A,A),(A,A,A↖{-}),(A,A↖{-},A),(A,A↖{-},A↖{-}),(A↖{-},A,A),(A↖{-},A,A↖{-}),(A↖{-},A↖{-},A),(A↖{-},A↖{-},A↖{-})\}$
- Chacun des prélèvements constitue une épreuve de Bernoulli de paramètre $p=0,84$ et dont le succès est A.
Les 3 prélèvements sont indépendants, et X compte le nombre de succès.
Par conséquent X est une binomiale de paramètres 3 et 0,84.
Soit: $X=B (\,3\,;\,0,84\,)$ - On cherche: $p((A,A↖{-},A↖{-}))=p(A)×p(A↖{-})×p(A↖{-})=0,84×0,16×0,16=0,021504$
- On cherche: $p((A↖{-},A,A↖{-})==p(A↖{-})×p(A)×p(A↖{-})=0,16×0,84×0,16=0,021504$
On retrouve le résultat précédent.
Propriété
Soit $n∈\ℕ^{*}$ et $k∈\ℕ$ avec $0≤ k≤ n$.
L'entier naturel donnant le nombre de chemins réalisant $k$ succès pour $n$ répétitions
sur l'arbre d'un schéma de Bernoulli de paramètres n et p se note $(\table n; k)$
On l'appelle coefficient binomial $(\table n; k)$
On dit aussi " nombre de combinaisons de $k$ objets parmi $n$" .
Par convention: $(\table 0; 0)=1$
On obtient directement les coefficients binomiaux avec les calculatrices:
Casio: OPTN PROB n nCr k
TI: MATH PRB n Combinaison k
Exemple
On reprend l'exemple précédent.
Dénombrer le nombre d'événements donnant exactement 1 composant conforme.
Citer les tous.
Corrigé
On cherche le nombre de chemins réalisant $1$ succès pour $3$ répétitions
sur l'arbre précédent.
Il est égal à $(\table 3; 1)=3$
Il s'agit de $(A,A↖{-},A↖{-})$, $(A↖{-},A,A↖{-})$ et $(A↖{-},A↖{-},A)$.
Propriété
$(\table n; 0)=1$ $(\table n; 1)=n$
Propriété de symétrie
Pour tous les entiers $n$ et $k$ tels que $0≤k≤n$
$(\table n; k)=(\table n; n-k)$
Relation de Pascal
Pour tous les entiers $n$ et $k$ tels que $0$<$k$<$n$
$(\table n; k)=(\table n-1; k-1)+(\table n-1; k)$
Exemple
Cet exercice se fait sans calculatrice, et en utilisant les propriétés précédentes.
On suppose que $(\table 12; 2)=66$, $(\table 13; 3)=286$, $(\table 13; 4)=715$ et $(\table 14; 6)=3003$.
- Déterminer $(\table 13; 10)$, $(\table 14; 4)$ et $(\table 12; 3)$
- On pose $s=(\table 5; 5)+(\table 6; 5)+(\table 7; 5)+...(\table 12; 5)+(\table 13; 5)$
Démontrer à l'aide de la relation de Pascal que $s=3003$
Corrigé
-
Par symétrie, on a: $(\table 13; 10)=(\table 13;13- 10)$
Soit: $(\table 13; 10)=(\table 13;3)=$$286$
D'après la relation de Pascal, on a: $(\table 14; 4)=(\table 13; 3)+(\table 13; 4)=286+715=$$1001$
D'après la relation de Pascal, on a: $(\table 13; 3)=(\table 12; 2)+(\table 12; 3)$
Et donc: $(\table 12; 3)=(\table 13; 3)-(\table 12; 2)=286-66=$$220$ - D'après la relation de Pascal, on a:
$(\table 6; 6)+(\table 6; 5)=(\table 7; 6)$
Et donc: $(\table 6; 5)=(\table 7; 6)-(\table 6; 6)$
De même, on obtient: $(\table 7; 5)=(\table 8; 6)-(\table 7; 6)$ et $(\table 8; 5)=(\table 9; 6)-(\table 8; 6)$ ...etc... $(\table 13; 5)=(\table 14; 6)-(\table 13; 6)$
Donc: $s=(\table 5; 5)+(\table 7; 6)-(\table 6; 6)+(\table 8; 6)-(\table 7; 6)...+(\table 14; 6)-(\table 13; 6)$
On constate que, par un jeu de dominos, presque tous les termes s'annulent. Il reste:
$s=(\table 5; 5)-(\table 6; 6)+(\table 14; 6)$
Or, on a: $(\table 5; 5)=(\table 6; 6)=1$
Et par ailleurs, on sait que: $(\table 14; 6)=3003$
Donc: $s=3003$
Propriété
Si $X=B (n,p)$, et $0≤ k≤ n$, alors $p(X=k)=(\table n; k)\,p^k(1-p)^{n-k}$ .
En pratique, on obtient directement les valeurs de $p(X=k)$ avec les calculatrices:
Casio: STAT DIST BinomialPD($k,n,p$)
TI: 2nd distrib binomFdp($n,p,k$)
De même pour les valeurs de $p(X≤k)$:
Casio: STAT DIST BinomialCD($k,n,p$)
TI: 2nd distrib binomFrép($n,p,k$)
Exemple
On reprend encore l'exemple précédent.
- Donner la formule donnant la probabilité qu'exactement 2 composants soient acceptés, puis déterminer la valeur de cette probabilité (arrondie à 0,0001 près).
- Déterminer la probabilité (arrondie à 0,0001 près) qu'au moins 1 composant soit accepté.
Corrigé
-
On cherche $p(X=2)$. On a: $p(X=2)=(\table 3; 2)\,0,84^2(1-0,84)^{3-2}=3×0,84^2×0,16≈0,3387$.
A la calculatrice, on peut obtenir directement: $p(X=2)≈0,3387$. -
On cherche $p(X≥1)$.
Or $p(X≥1)=1-p(X\text"<"1)=1-p(X=0)$.
Et à la calculatrice, on obtient: $p(X=0)≈0,0041$.
Donc $p(X≥1)≈0,9959$.
Exemple
$9\%$ de la population française est du groupe B.
Dans une ville isolée du massif central, on choisit au hasard 20 personnes.
La population de la ville est suffisamment importante pour que l'on puisse considérer qu'il s'agit de tirages avec remise.
Parmis les 20 personnes, 6 sont du groupe B. Ce nombre semble élevé,
et l'on peut se demander si $9\%$ de la population de cette ville est du groupe B.
- Soit X le nombre de personnes du groupe B dans un échantillon de 20 personnes. Quelle est la loi de X?
- Déterminer le plus petit entier $a$ tel que $p(X≤ a)\text">"0,025$.
- Déterminer le plus petit entier $b$ tel que $p(X≤ b)≥0,975$.
- Montrer que $p(a≤X≤b)≥0,95$
- Le maire de la ville affirme que, dans sa ville, le pourcentage de la population de groupe B n'est sans doute pas de $9\%$. Il précise même que son affirmation est certaine à plus de $95\%$.
Justifier ces affirmations par des considérations mathématiques.
Corrigé
- Le choix de chacune des 20 personnes constitue une épreuve de Bernoulli de paramètre $p=0,09$ et dont le succès est l'appartenance au groupe B.
Les choix sont considérés comme indépendants (comme des tirages avec remise), et X compte le nombre de succès.
Par conséquent X est une binomiale de paramètres $n=20$ et $p=0,09$.
On note: $X=B(20;0,09)$. - A la calculatrice: $p(0≤ X≤0)≈0,1516$. Donc $a=0$.
- A la calculatrice: $p(0≤ X≤4)≈0,9709$, $p(0≤ X≤5)≈0,9932$. Donc $b=5$.
- $a$ est le plus petit entier tel que $p(X≤ a)\text">"0,025$,
donc $p(X\text"<"a)≤0,025$, et donc $-p(X\text"<"a)≥-0,025$.
De plus $p(X≤ b)≥0,975$.
Et comme $p(a≤X≤b)=p(X≤b)-p(X\text"<"a)$,
on obtient: $p(a≤X≤b)≥0,975-0,025$, soit $p(a≤X≤b)≥0,95$.
Autre méthode: on calcule directement $p(a≤X≤b)=p(0≤X≤5)≈0,9932$
Donc $p(a≤X≤b)≥0,95$ - Dans l'échantillon de 20 personnes, on a: $X=6$. Or cette valeur n'est pas comprise dans $[a;b]$.
D'après ce qui précède, ce cas de figure arrive dans moins de $5\%$ des cas (pour $p$ effectivement égal à $9\%$).
Donc le maire peut, à juste titre, rejeter l'hypothèse que $9\%$ de la population de la ville isolée soit du groupe B , le risque qu'il a de se tromper est inférieur à $5\%$.
Comme 6 est au dessus de l'intervalle de fluctuation de X, la proportion de personnes de groupe B est sans doute supérieure à $9\%$.
Conséquence
Si $X$ suit la loi binomiale de paramètres n et p, alors:
son espérance est: $E(X)=np$
sa variance est: $V(X)=np(1-p)$
son écart-type est: $σ(X)=√ {np(1-p)}$
Exemple
On pose: $X=B(100;0,41)$ et $X=B(50;0,78)$
Calculer les espérances et les variances de X et Y. Comparer ces variables aléatoires.
Corrigé
$E(X)=100×0,41=41$ $E(Y)=50×0,78=39$
Ces valeurs sont proches. En moyenne, sur un grand nombre d'expériences, les valeurs prises par ces variables aléatoires seront sans doute proches.
$V(X)=100×0,41×(1-0,41)=24,19$ $V(Y)=50×0,78×(1-0,78)=8,58$
La variance de X est environ trois fois plus grande que celle de Y. Le risque que la variable aléatoire s'éloigne de sa moyenne est beaucoup plus grand pour X que pour Y.
III Loi géométrique
Définition
On repète une épreuve de Bernoulli de paramètre $p$ un nombre suffisant de fois pour obtenir au moins un "succès".
La loi géométrique de paramètre $p$ est la loi de la variable aléatoire X qui donne le rang du premier "succès".
On dit aussi que X donne le temps d'attente du premier "succès".
On note: $X=G (p)$.
Pour tout naturel non nul $k$, on a: $p(X=k)=pq^{k-1}$ (où $q=1-p$)
Propriété
Si $X$ suit la loi géométrique de paramètre p, alors:
son espérance est: $E(X)={1}/{p}$
Exemple
On lance un dé un nombre suffisant de fois pour obtenir au moins un 5. Soit X la variable aléatoire qui donne le rang du premier 5 obtenu.
X suit la loi géométrique de paramètre $p={1}/{6}$.
Pour tout naturel non nul $k$, on a: $p(X=k)={1}/{6}×({5}/{6})^{k-1}$
On a également: $E(X)={1}/{p}=6$
Le temps d'attente moyen du premier 5 est de 6 lancers.
Perte de mémoire
Si $X$ suit la loi géométrique de paramètre p, alors:
pour tous entiers naturels $k$ et $k'$ $p_{X\>k}(X\>k+k')=p(X\>k')$
On dit que le temps d'attente d'un succès ne dépend pas du temps d'attente "passé".
Exemple
On reprend l'exemple ci-dessus, dans lequel on lance un dé un nombre suffisant de fois pour obtenir au moins un 5.
On rappelle que $p={1}/{6}$ et $q={5}/{6}$
Montrer que $p(X≤7)=1-q^7$.
En déduire l'expression de $p(X\>7)$ en fonction de $q$.
A l'aide des formules sur les probabillités conditionnelles, calculer $p_{X\>10}(X\>17)$ en fonction de $q$.
Vérifier la propriété d'absence de mémoire.
Corrigé
X suit la loi géométrique de paramètre $p={1}/{6}$ (et on a: $q={5}/{6}$).
On a alors: $p(X≤7)=p(X=1)+p(X=2)+...+p(X=7)=p+pq+pq^2+...+pq^6$
Soit: $p(X≤7)=p(1+q+q^2+...+q^6)=p{1-q^7}/{1-q}$
Soit: $p(X≤7)=p{1-q^7}/{p}=1-q^7$
On obtient alors: $p(X\>7)=1-p(X≤7)=1-(1-q^7)=q^7$
On a: $p_{X\>10}(X\>17)={p(X\>10 \,et\,X\>17)}/{p(X\>10)}$
Soit: $p_{X\>10}(X\>17)={p(X\>17)}/{p(X\>10)}$
Or, comme précédemment, on obtient: $p(X\>17)=q^{17}$ et $p(X\>10)=q^{10}$
Donc finalement: $p_{X\>10}(X\>17)={q^{17}}/{q^{10}}=q^7$
On a par conséquent: $p_{X\>10}(X\>17)=p(X\>7)$
Soit: $p_{X\>10}(X\>10+7)=p(X\>7)$
Cela confirme la véracité de la propriété d'absence de mémoire.
On aurait pu remplacer 7 par n'importe quel naturel non nul. Ce n'est donc pas parce qu'on a déjà attendu, en vain, pendant 10 lancers l'arrivée d'un premier 5,
qu'on peut espérer que le délai avant qu'arrive effectivement le premier 5 soit plus faible qu'au moment du premier lancer. Et on peut aussi remplacer 10 par n'importe quel autre naturel non nul. La perte de mémoire est effective!