 Dérivées, convexité
Dérivées, convexité
A SAVOIR: le cours sur Dérivées, convexité
Exercice 2
Cet exercice utilise parfois des fonctions vues en terminale.
Les questions 3. à 5. : utilisent la fonction logarithme népérien
Déterminer $f\,'$, puis le signe de $f\,'$ sur I, et dresser alors le tableau de variation de $f$ sur l'intervalle I (sans les limites) dans chacun des cas suivants:
- $f(x)=5e^{-x^2+1}$ sur $I=\R$
- $f(x)=e^{5x+1}+6x$ sur $I=\R$
- $f(x)=e^{5x+1}-6x$ sur $I=\R$
- $f(x)=5x\ln x+x$ sur $I=]0;+∞[$
- $p(x)=\ln (-3x+5)$ avec $I=[0;{5}/{3}[$
Corrigé
- $f(x)=5e^{-x^2+1}$ sur $I=\R$.
On pose $f=ke^u$ avec $k=5$ et $u=-x^2+1$.
D'où $f\,'=ku'e^u$ avec $u'=-2x$.
Soit $f\,'(x)=5×(-2x)×e^{-x^2+1}=-10xe^{-x^2+1}$.
$f\,'$ est un produit de 2 facteurs.
$-10x$ est linéaire, de coefficient $-10$ strictement négatif, et s'annule pour $x=0$.
$e^{-x^2+1}$ est une exponentielle, et donc strictement positive.
D'où le tableau de variation de $f$ sur I.
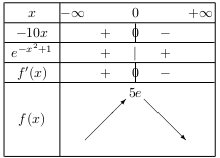
- $f(x)=e^{5x+1}+6x$ sur $I=\R$.
On pose $f=e^u+6x$ avec $u=5x+1$.
D'où $f\,'=u'e^u+6$ avec $u'=5$.
Soit $f\,'(x)= 5e^{5x+1}+6$.
$f\,'$ est une somme de termes.
L'exponentielle $e^{5x+1}$ est strictement positive et 5 également.
Donc le premier terme $5e^{5x+1}$ est strictement positif.
Or le second terme 6 est strictement positif.
Donc $f\,'$ est strictement positive.
D'où le tableau de variation de $f$ sur I.
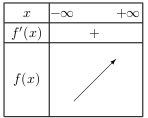
- $f(x)=e^{5x+1}-6x$ sur $I=\R$.
On pose $f=e^u-6x$ avec $u=5x+1$.
D'où $f\,'=u'e^u-6$ avec $u'=5$.
Soit $f\,'(x)= 5e^{5x+1}-6$.
$f\,'$ est une somme de termes.
Mais $5e^{5x+1}\text">"0$ alors que $-6\text"<"0$.
On va chercher pour quels $x$ l'expression $5e^{5x+1}-6$ est positive.
Par conséquent, on résout $5e^{5x+1}-6\text">"0$.
Soit $5e^{5x+1}-6\text">"0⇔5e^{5x+1}\text">"6⇔e^{5x+1}\text">"{6}/{5}$
Soit $5e^{5x+1}-6\text">"0⇔\ln(e^{5x+1})\text">"\ln({6}/{5})⇔5x+1\text">"\ln(1,2)$
Soit $5e^{5x+1}-6\text">"0⇔5x\text">"\ln(1,2)-1⇔x\text">"{\ln(1,2)-1}/{5}$
De même, on obtient $5e^{5x+1}-6=0⇔x={\ln(1,2)-1}/{5}$
D'où le tableau de variation de $f$ sur I.
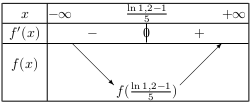
- $f(x)=5x\ln x+x$ sur $I=]0;+∞[$.
On pose $f=uv+x$ avec $u=5x$ et $v=\ln x$.
D'où $f\,'=u'v+uv'+1$ avec $u'=5$ et $v'={1}/{x}$.
Soit $f\,'(x)=5\lnx +5x{1}/{x}+1=5\ln x+5+1=5\ln x+6$.
$f\,'$ est une somme de termes.
6>0, mais le signe de $5\ln x$ est variable.
On va chercher pour quels $x$ l'expression $5\ln x+6$ est positive.
Par conséquent, on résout $5\ln x+6\text">"0$.
$5\ln x+6\text">"0⇔\ln x\text">"{-6}/{5}⇔e^{\ln x}\text">"e^{{-6}/{5}}⇔x\text">"e^{-1,2}$.
De même, on obtient $5\ln x+6=0⇔x=e^{-1,2}$.
D'où le tableau de variation de $f$ sur I.
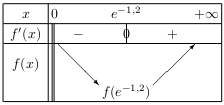
- Dérivons $p(x)=\ln (-3x+5)$
On pose $u(x)=-3x+5$. Donc $u\,'(x)=-3$.
ici $p(x)= \ln u$. Donc $p\,'(x)={u\,'}/{u}$.
Donc $p\,'(x)={-3}/{-3x+5}$.
$p\,'(x)$ est un quotient dont nous allons trouver les signes du dénominateur et du numérateur.
La fonction affine $-3x+5$ s'annule en ${5}/{3}$, et est strictement positive pour $x$<${5}/{3}$.
Donc, sur I: $-3x+5$>$0$.
Or $p\,'$ a pour numérateur $-3$ qui est strictement négatif.
Finalement, sur $I$, $p\,'(x)$<$0$.
Donc $p$ est strictement décroissante sur I.