 Fonction logarithme népérien
Fonction logarithme népérien
A SAVOIR: le cours sur la fonction ln
Exercice 9
Cet exercice, très technique, n'est là que pour les plus curieux...
Construction de la table de "logarithmes" de Neper
On a vu dans l'exercice 8 que Neper avait inventé une fonction dont l'expression moderne est la suivante:
$Nep(z)=10^7\ln({{10^7}/{z})$ (pour tout réel $z$ strictement positif)
Neper ne connaissait évidemment pas cette expression. Néanmoins,il a réussi a dresser un tableau de valeurs très précis de cette fonction $Nep$.
Voyons comment il a procédé.
Partie A Une propriété essentielle
1.a. On pose: $g(a)=a-1-\ln(a)$ définie pour $a>0$. Montrer que $g'(a)={a-1}/{a}$, puis dresser le tableau de variation de $g$.
1.b. En déduire que $\ln a≤a-1$ pour tout $a>0$.
1.c. Poser $a={1}/{b}$ dans l'inégalité précédente. Montrer que: ${b-1}/{b}≤\ln b$ pour tout $b>0$.
2. On a donc montré que: ${z-1}/{z}≤\ln z≤z-1$ pour tout $z>0$.
Poser $z={10^7}/{x}$ dans l'inégalité double ci-dessus. Montrer que: $10^7-x≤Nep(x)≤10^7{10^7-x}/{x}$
Neper avait évidemment obtenu ce résultat par d'autres moyens... Il a raisonné par des considérations physiques sur des vitesses (voir exercice 8)
Partie B Construction de la première table de Neper
1. D'après la propriété ci-dessus, on sait que, si $x>0$ alors $10^7-x≤Nep(x)≤10^7{10^7-x}/{x}$
Expliquer pourquoi Neper a proposé que: $Nep( 9\, 999\, 999)≈1,000\, 000\, 05$
Neper peut alors commencer à remplir sa table.
Il sait donc que: $Nep( 10^7)=0$ (voir exercice 8).
Il vient de prouver que: $Nep( 9\, 999\, 999)≈1,000\, 000\, 05$ (voir ci-dessus).
Neper a donc les deux premières images du tableau de valeurs ci-dessous.

Les $x$ sont calculés en gardant 7 chiffres après la virgule. Les $y$ sont calculés en gardant 8 chiffres après la virgule.
Neper continue alors son tableau en considérant la suite géométrique $(g_n)$ de raison $q={9\,999\,999}/{10^7}=0,999\,999\,9=1-10^{-7}$ et de premier terme $g_0=10^7$.
Les valeurs de la suite $(g_n)$ se trouvent dans la ligne des $x$ (en rouge).
On a donc: $g_0=10^7$, $g_1=9\, 999\, 999$.
La raison $q=1-10^{-7}$ semble bien compliquée! Neper l'a choisie pour 2 raisons. La première est que les termes sont quasiment des entiers naturels. La seconde
est que les termes successifs sont très faciles à calculer grâce à la propriété suivante.
Pour tout $x$, on a: $x×q=x×(1-10^{-7})=x-{x}/{10^7}$.
2.
Déterminer, sans calculatrice, mais à l'aide de la propriété ci-dessus, les termes $g_2$ et $g_3$ (à $10^{-7}$ près).
Neper calcule ainsi toutes les valeurs jusqu'à $g_{100}≈9\,999\,900,000\,495\,00$.
3.
On a vu dans l'exercice 8 que la fonction de Neper "transformait" une suite géométrique en suite arithmétique.
Quelle est la raison de la suite arithmétique $(Nep(g_n))$ dans cette première table?
4. En déduire, sans calculatrice, les valeurs de $Nep(g_2)$ et $Nep(g_3)$ (à $10^{-7}$ près).
Neper calcule ainsi les images des $g_n$ jusqu'à $Nep(g_{100})≈100,000\,005\,0$.
On remarquera que la difficulté n'est pas de trouver les images, mais de trouver les antécédents!
Partie C Construction des autres tables de Neper
Neper veut alors commencer une seconde table dont les 2 premiers $x$ sont $10^7$ et $9\,999\,900$.
Chacun aura remarqué que $9\,999\,900$ est approximativement le dernier $x$ de la première table...
Il a donc besoin de l'image de $9\,999\,900$, et il désire une certaine précision.
Il considère alors que les variations des images sont quasiment proportionnelles aux variations des antécédents.
Pour information, on dit que Neper procède par interpolation linéaire.
Cela est valide à condition que la courbe représentant la fonction $Nep$ soit quasiment droite entre les antécédents, ce qui est le cas puisque ces derniers sont grands et suffisamment proches.
Neper a obtenu: $g_{100}≈9\,999\,900,000\,495\,0$ et $g_{101}≈9\,999\,899,000\,505\,0$
ainsi que leurs images: $Nep(g_{100})≈100,000\,005\,00$ et $Nep(g_{101})≈101,000\,005\,05$,
Il dispose donc du tableau de valeurs suivant.

1. Vérifier alors que Neper obtient: $Nep(9\,999\,900)≈1,000\,500\,0$ (à $10^{-7}$ près).
Comme précédemment, Neper remplit alors une seconde table. Cette fois-ci, les 2 premiers antécédents sont $10^7$ et $9\,999\,900$.

2. Quelle est la raison de la suite géométrique dans cette table?
Quelle est la raison de la suite arithmétique dans cette table?
Cette table contiendra 51 images. La dernière est $Nep(9\,995\,001,224\,804\,04)≈5\,000,025\,000\,00$
On notera que les images de la première table étaient approximativement les entiers de 0 à 100, et que les images de cette seconde table sont approximativement les centaines de 100 à $5\,000$.
Et Neper construisit ainsi 69 tables jusqu'à l'image de $5\,000\,000$.
Partie D Construction de la table des images des sinus
Neper avait donc à sa disposition 69 tables donnant des images par sa fonction $Nep$ de nombres compris entre $10\,000\,000$ et $5\,000\,000$.
Son objectif était de faciliter (pour les astronomes en particulier) les calculs impliquant des sinus.
Et ses tables lui suffisaient pour trouver l'image de n'importe quel sinus.
On rappelle ici qu'un sinus d'angle n'était pas considéré comme un nombre (sans unité), mais comme la longueur du côté opposé à l'angle dans un triangle rectangle dont la longueur de l'hypoténuse était fixée (souvent très grande).
Par exemple, pour un rayon de $10^7$, le sinus de l'époque valait $10^7$ fois le sinus actuel.
D'où ces valeurs de $x$ "astronomiques"...
Neper a ainsi déterminé les images des sinus de tous les angles entre 30° et 90°, à la minute près (pour les images des angles inférieurs à 30°, NEPER a utilisé des formules de trigonométrie).
Evidemment, quand un sinus était situé entre 2 valeurs de sa table, il procédait par interpolation linéaire pour trouver son image (son "logarithme").
Une anecdote. Ce sont ces "sinus" entiers qui sont le point de départ des calculs de Neper ; c’est pourquoi il les appelle nombres naturels, par opposition aux nombres artificiels ou logarithmes, qui sont ceux de la suite arithmétique. Neper est passé du discret des nombres (arithmos) au continu de grandeurs qu'on ne savait exprimer qu'en termes de rapports (logos); d'où le nom de logarithme!
Un exemple.
Neper sait que le "sinus" de 89° vaut environ $9\,998\,477$ (en fait, c'est $10^7$ fois le sinus actuel).
Déterminer $Nep(9\,998\,477)$ sachant que: $Nep(9\,998\,400)≈1\,600$ et $Nep(9\,998\,500)≈1\,500$
Partie E Quelques propriétés
On remarquera que la fonction de Neper n'est pas la fonction $\ln$. C'est pourquoi, contrairement aux idées reçues, la proposition "$Nep(ab)=Nep(a)+Nep(b)$ pour tous $a$ et $b$ strictement positifs" est fausse.
En fait, le but de Neper n'était pas de "transformer des produits en sommes", mais d'alléger les calculs sur les sinus.
Et sa fonction, étudiée en conséquence, a donc d'autres qualités. Par exemple, celles citées dans les 2 questions qui suivent sont très pratiques dans les calculs trigonométriques.
On rappelle que $Nep(z)=10^7\ln({{10^7}/{z})$
1. Vérifier, en utilisant l'expression de $Nep(z)$, que:
si ${a}/{b}={c}/{d}$, alors $Nep(a)-Nep(b)=Nep(c)-Nep(d)$.
2. En déduire que:
si $a^2=bc$, alors $Nep(a)={Nep(b)+Nep(c)}/{2}$.
Cette propriété, essentielle pour Neper, facilite les calculs avec les radicaux.
Par exemple, pour déterminer la valeur de $√{21}$, on procède comme suit. Comme $(√{21})^2=21=3×7$, on a: $Nep(√{21})={Nep(3)+Nep(7)}/{2}$.
La table donne $Nep(3)$ et $Nep(7)$. On en fait la moyenne. Et par lecture inverse de la table, on obtient $√{21}$.
3. Vérifier , en utilisant l'expression de $Nep(z)$, que:
pour tous $a$ et $b$ strictement positifs, , $Nep(a)+Nep(b)=Nep({a×b}/{10^7})$.
Cette propriété facilite les calculs de produits.
Par exemple, pour déterminer la valeur de $3,2×9,4$, on procède comme suit. La table donne $ Nep(3,2)≈1,495×10^8$ et $Nep(9,4)≈1,388×10^8$. On en fait la somme, qui vaut environ $2,883×10^8$.
Et par lecture inverse de la table, on obtient ${3,2×9,4}/{10^7}≈3,008×10^{-6}$. Il reste à multiplier le résultat par $10^7$ pour avoir le produit, soit 30,08.
Ce n'est pas très pratique. Henry Briggs et Neper en discuteront. Et Briggs publiera des tables de la fonction: $Brig(x)=10^{14}{ \ln{x}}/{\ln 10}$, qui vérifie: $Brig(a)+Brig(b)=Brig(ab)$.
Corrigé
Partie A Une propriété essentielle
1.a. On pose: $g(a)=a-1-\ln(a)$ définie pour $a>0$.
Donc: $g'(a)=1-0-{1}/{a}={a}/{a}-{1}/{a}={a-1}/{a}$.
D'où le tableau de signe de $g'$ et le tableau de variation de $g$.
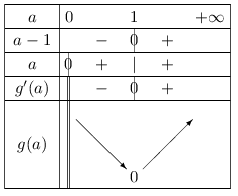
1.b. D'après le tableau ci-dessus, le minimumm de $g$ est 0.
Donc, $0≤g(a)$ pour tout $a>0$.
Soit: $0≤a-1-\ln a$ pour tout $a>0$.
Et donc: $\ln a≤a-1$ pour tout $a>0$. c.q.f.d.
1.c. On pose $a={1}/{b}$ dans l'inégalité précédente. On obtient:
$\ln {1}/{b}≤{1}/{b}-1$
Soit: $\ln 1-\ln b≤ {1}/{b}-{b}/{b}$
Soit: $-\ln b≤ {1-b}/{b}$
Donc: $-{1-b}/{b}≤ \ln b$
Soit: ${b-1}/{b}≤\ln b$ (pour tout $b>0$).
2. On a donc montré que: ${z-1}/{z}≤\ln z≤z-1$ pour tout $z>0$.
On pose $z={10^7}/{x}$ dans l'inégalité double ci-dessus.
On obtient: ${{10^7}/{x}-1}/{{10^7}/{x}}≤\ln {10^7}/{x}≤{10^7}/{x}-1$
On multiplie chacun des membres par $10^7$. On obtient:
$10^7×({{10^7}/{x}-1})×{{x}/{10^7}}≤10^7\ln {10^7}/{x}≤10^7{10^7}/{x}-1$
Soit: $10^7-x≤Nep(x)≤10^7{10^7-x}/{x}$ c.q.f.d.
Partie B Construction de la première table de Neper
1. On applique la propriété ci-dessus pour $x=9\, 999\, 999$.
On obtient: $10^7-9\, 999\, 999≤Nep(9\, 999\, 999)≤10^7{10^7-9\, 999\, 999}/{9\, 999\, 999}$
Soit: $1≤Nep(9\, 999\, 999)≤10^7{1}/{9\, 999\, 999}$
Soit: $1≤Nep(9\, 999\, 999)≤1,000\, 000\, 10$
Neper a alors pris le milieu de l'encadrement ci-dessus pour valeur approchée de $Nep( 9\, 999\, 999)$.
Soit: $Nep( 9\, 999\, 999)≈1,000\, 000\, 05$
2. On a : $g_0=10^7$, $g_1=9\, 999\, 999$.
Or, pour tout $x$, on a: $x×q=x×(1-10^{-7})=x-{x}/{10^7}$.
On a alors: $g_2=g_1×q=g_1-{g_1}/{10^7}=9\, 999\, 999-{9\, 999\, 999}/{10^7}=9\, 999\, 999-0,9\, 999\, 999=9\, 999\, 998,000\,000\,1$
Et de même: $g_3≈9\, 999\, 998,000\,000\,1-0,9\, 999\, 998≈9\, 999\, 997,000\,000\,3 $ (à $10^{-7}$ près).
On le vérifie dans le tableau proposé...

3.
On sait que la fonction de Neper transformait une suite géométrique en suite arithmétique.
Ici, la suite arithmétique des images $(Nep(g_n))$ a pour raison:
$r=(Nep(g_1)$-$(Nep(g_0)≈1,000\, 000\, 05-0≈$$1,000\, 000\, 05$
4. On obtient donc: $Nep(g_2)≈Nep(g_1)+1,000\, 000\, 05≈1,000\, 000\, 05+1,000\, 000\, 05≈2,000\, 000\, 10$
Et: $Nep(g_3)≈Nep(g_2)+1,000\, 000\, 05≈2,000\, 000\, 10+1,000\, 000\, 05≈3,000\, 000\, 15$
Partie C Construction des autres tables de Neper
1.
On a le tableau de valeurs suivant.

On procède par interpolation linéaire (ce qui revient à assimler un morceau de courbe à un segment).
Les variations des $y$ sont proportionnelles aux variations des $x$.
On obtient donc: ${Nep(9\,999\,900)-100,000\,005\,00}/{9\,999\,900-9\,999\,900,000\,495\,0}≈{101,000\,005\,05-100,000\,005\,00}/{9\,999\,899,000\,505\,0-9\,999\,900,000\,495\,0}$
Oui, je sais, c'est horrible! Neper savait compter...
On en déduit: $Nep(9\,999\,900)≈100,000\,005\,00-0,000\,495\,0×{1,000\,000\,05}/{-0,999\,99}≈1,000\,500\,0$ (à $10^{-7}$ près).
2.
Les 2 premiers antécédents de la seconde table sont $10^7$ et $9\,999\,900$.

La raison de la suite géométrique est: ${9\,999\,900}/{10^7}=0,9\,999\,900$
La raison de la suite arithmétique est: $100,000\,5000\,0-0=100,000\,5000\,0$
Cette table contiendra 51 images. Si l'on conserve 7 chiffres après la virgule pour les $x$, la dernière image est $Nep(9\,995\,001,224\,801\,8)≈5\,000,025\,000\,00$
On notera que les images de la première table sont approximativement les entiers de 0 à 100, et que les images de la seconde table sont approximativement les centaines de 100 à $5\,000$.
Partie D Construction de la table des images des sinus
On procède par interpolation linéaire.
On a: $Nep(9\,998\,400)≈1\,600$ et $Nep(9\,998\,500)≈1\,500$
Une hausse de 100 sur les $x$ correspond à une baisse de 100 sur les $y$.
Donc $Nep(9\,998\,477)≈1\,600-477≈1\,523$.
Partie E Quelques propriétés
$Nep(z)=10^7\ln({{10^7}/{z})$ (pour tout réel $z$ strictement positif)
1. On suppose que: ${a}/{b}={c}/{d}$.
On calcule alors: $Nep(a)-Nep(b)=10^7\ln({{10^7}/{a})-10^7\ln({{10^7}/{b})=10^7(\ln({{10^7}/{a})-\ln({{10^7}/{b}))$
Donc: $Nep(a)-Nep(b)=10^7\ln({10^7}/{a}×{b}/{10^7})=10^7\ln({a}/{b})$
De même, on obtient: $Nep(c)-Nep(d)=10^7\ln({c}/{d})$
Or, on sait que: ${a}/{b}={c}/{d}$.
Donc on obtient: $Nep(a)-Nep(b)=Nep(c)-Nep(d)$. c.q.f.d.
2. On suppose que: $a^2=bc$. Donc: ${a}/{b}={c}/{a}$.
Donc, en utilisant la propriété précédente, on obtient:
$Nep(a)-Nep(b)=Nep(c)-Nep(a)$
Donc: $2Nep(a)=Nep(b)+Nep(c)$
Et donc: $Nep(a)={Nep(b)+Nep(c)}/{2}$.
3. On a: $Nep(a)+Nep(b)=10^7\ln({{10^7}/{a})+10^7\ln({{10^7}/{b})=10^7\ln({10^7}/{a}×{10^7}/{b})$
Soit: $Nep(a)+Nep(b)=10^7\ln({10^{14}}/{ab})$
Or $Nep({a×b}/{10^7})=10^7\ln({{10^7}/{{a×b}/{10^7}})=10^7\ln({10^{14}}/{ab})$
Donc: $Nep(a)+Nep(b)=Nep({a×b}/{10^7})$