 Statistique à deux variables quantitatives
Statistique à deux variables quantitatives
A SAVOIR: le cours sur Statistique à deux variables quantitatives
Exercice 2
Un chercheur veut modéliser la courbe de croissance d'une souris dont il a modifié l'un des gènes.
Ses mesures sont résumées dans le tableau ci-dessous.

Pour $i$ allant de 1 à 10, $x_i$ donne le rang du jour, et $y_i$ est la masse (en grammes) de la souris pour le jour de rang $x_i$.
Le nuage de points correspondant à la série des $(x_i;y_i)$ pour $i$ allant de 1 à 10 est le suivant.
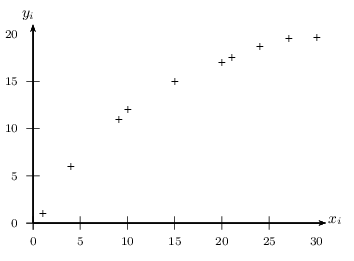
- La forme du nuage suggère-t-elle qu'un ajustement est possible?
Pour quelle raison? - Le chercheur pose: $z_i=e^{{y_{i}}/{8}}$ pour $i$ allant de 1 à 10.
Il décide d'étudier la série des $(x_i;z_i)$.
Compléter le tableau suivant.

- Représenter le nuage de points de la série des $(x_i;z_i)$.
- Déterminer à l'aide de votre calculatrice une équation de la droite de régression de $z$ en $x$ (les coefficients seront arrondis à 0,01 près).
- Déterminer à l'aide de votre calculatrice le coefficient de corrélation linéaire $r$ de la série double (arrondi à 0,001 près).
L'ajustement est-il satisfaisant. Pourquoi? - Le chercheur en déduit alors une formule permettant d'estimer la masse $y$ de la souris en fonction du rang $x$ du jour.
Déterminer cette formule. - Estimer par un calcul la masse $y$ de la souris (arrondi à 0,1 gramme près) pour le jour de rang 35.
Corrigé
- La forme du nuage laisse penser qu'un ajustement n'est pas possible.
Par contre, un ajustement par une "courbe" semble opportun. - On pose: $z_i=e^{{y_{i}}/{8}}$ pour $i$ allant de 1 à 10.
Ainsi, $z_1=e^{{1}/{8}}≈1,1$ et $z_{10}=e^{{19,6}/{8}}≈11,6$.
D'où le tableau complété.

- Voici le nuage de points de la série des $(x_i;z_i)$.
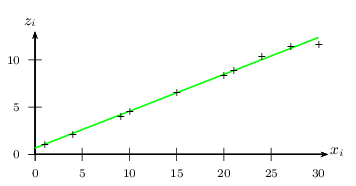
- A l'aide de la calculatrice, on trouve que la droite de régression de $z$ en $x$ a pour équation: $z=ax+b$, avec $a≈0,39$ et $b≈0,67$.
Elle est tracée en vert ci-dessus (non demandé). - A l'aide de la calculatrice, on trouve que le coefficient de corrélation linéaire $r$ de la série double vérifie: $r≈0,997$.
C'est quasi parfait! On a largement $|r|>0,9$. L'ajustement est donc très satisfaisant. - On a alors: $z=0,39x+0,67$ et $z=e^{{y}/{8}}$
Donc: $e^{{y}/{8}}=0,39x+0,67$
Et donc: ${y}/{8}=\ln (0,39x+0,67)$
Et par là: $y=8\ln(0,39x+0,67)$
La courbe associée est représentée en vert ci-dessous (non demandé).
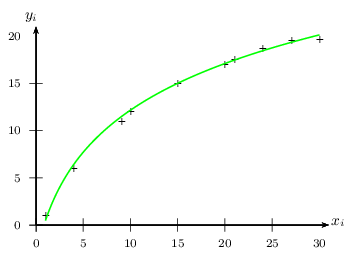
- Le jour de rang 35 donne $x=35$.
On calcule: $8\ln(0,39×35+0,67)≈21,3$
On peut espérer que la souris aura une masse d'environ 21,3 grammes pour le mois de rang 35.
Evidemment, cela suppose que le modèle reste valide à ce moment là, ce qui est loin d'être évident (la masse de la souris va sans doute se stabiliser, alors que la fonction d'ajustement ne fait que croître!)