 Statistique à deux variables quantitatives
Statistique à deux variables quantitatives
A SAVOIR: le cours sur Statistique à deux variables quantitatives
Exercice 3
Après la visite annuelle du médecin scolaire, un instituteur enseignant dans une classe unique d'un village de Bourgogne a collecté les masses de ses 10 élèves.
Puis il leur a donné un test de calcul. Il a alors relevé la série suivante.

Pour $i$ allant de 1 à 10, $x_i$ donne la masse (en kg) de l'élève $i$, et $y_i$ donne sa note au test.
Le nuage de points correspondant à la série des $(x_i;y_i)$ pour $i$ allant de 1 à 10 est le suivant.
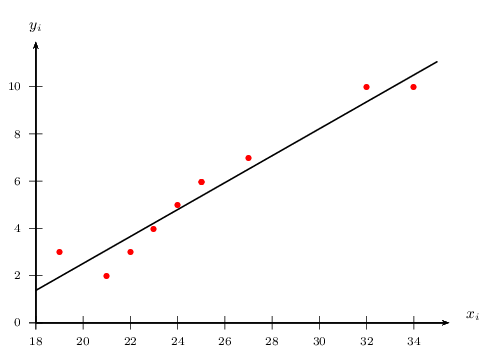
La droite de régression de $y$ en $x$ est tracée en noir.
- Déterminer à l'aide de votre calculatrice une équation de la droite de régression de $y$ en $x$ (les coefficients seront arrondis à 0,01 près).
- Déterminer à l'aide de votre calculatrice le coefficient de corrélation linéaire $r$ de la série double (arrondi à 0,001 près).
L'ajustement est-il satisfaisant. Pourquoi?
Y a-t-il une corrélation affine entre les notes et les masses? - L'instituteur se précipite alors chez le maire du village, et il lui demande de distribuer gratuitement chaque matin un petit déjeuner aux élèves.
Il prétend, sa série statistique à l'appui, que les performances scolaires de ses élèves sont indiscutablement liées à leurs masses.
Et il affirme que des élèves mieux nourris auront de meilleurs résultats!
Le maire lui répond immédiatement que ses statistiques ne prouvent rien...
Qu'en penser?
Corrigé
- A l'aide de la calculatrice, on trouve que la droite de régression de $y$ en $x$ a pour équation: $y=ax+b$, avec $a≈0,58$ et $b≈-8,89$.
- A l'aide de la calculatrice, on trouve que le coefficient de corrélation linéaire $r$ de la série double vérifie: $r≈0,968$.
C'est parfait! On a largement $|r|>0,9$. L'ajustement est donc très satisfaisant.
Il y a effectivement une corrélation affine entre les notes et les masses. - Le fait que deux variables soient « fortement corrélées » ne démontre pas qu'il y ait une relation de causalité entre l'une et l'autre.
Le contre-exemple le plus typique est celui où elles sont en fait liées par une causalité commune, liée à une troisième variable. Cette variable (cachée) s'appelle "variable de confusion".
Ici, c'est sans doute le cas.
Il s'agit d'une classe unique, où les âges des enfants varient beaucoup (de 6 à 12 ans pour simplifier).
On peut supposer que les enfants les plus jeunes, et donc les plus légers, ont eu plus de difficulté à réussir le test de calcul que leurs aînés, qui sont par ailleurs plus lourds que leurs cadets.
La causalité commune est en fait l'âge!
L'âge influe sur la masse et sur le succès au test.
Lier performance et masse est donc farfelu, et, dans ce cas, le maire a raison!
Il est néanmoins vraisemblable qu'une meilleure alimentation induit de meilleurs résultats scolaires, mais la série proposée ne permet pas de le prouver!