 Statistique à deux variables quantitatives
Statistique à deux variables quantitatives
A SAVOIR: le cours sur les Statistiques vu en classe de Seconde
Exercice 6
Voici un tableau de l'INSEE donnant la répartition du patrimoine brut des ménages français début 2018.
Pour information, le patrimoine brut correspond au montant total des actifs détenus par un ménage incluant la résidence principale, les éventuelles résidences secondaires
l’immobilier de rapport (c’est-à-dire rapportant un revenu foncier), les actifs financiers du ménage, et les actifs professionnels
lorsque le ménage a une activité d’indépendant à titre principal ou secondaire. Il inclut également le patrimoine "restant" : les biens durables (voiture, équipement de la maison, etc.),
les bijoux, les œuvres d’art et autres objets de valeur.


Par exemple, début 2018, les 10 % des ménages aux patrimoines les moins élevés détiennent un patrimoine brut moyen de $1\, 800$ euro.
- Recopier et compléter le tableau suivant, qui donne la part du patrimoine français en fonction de la tranche de la population.

Par exemple, début 2018, les 10 % des ménages les plus fortunés disposent d'environ 46,35 % du patrimoine brut total.
Les résultats seront arrondis à 0,01 % près (la valeur 0,06 % a été arrondie par défaut pour obtenir une somme de 100 %). - Recopier et compléter le tableau suivant, qui donne les fréquences cumulées croissantes associées au tableau précédent.

Les $x_i$ donnent les fréquences cumulées de la population (en %)
Les $y_i$ donnent les fréquences cumulées du patrimoine (en %)
Par exemple, début 2018, les 30 % des ménages les moins fortunés disposent d'environ 1,02 % du patrimoine brut total. -
Avec un tableur, représenter (dans un repère orthogonal) le polygone $P$ donnant la part du patrimoine brut total en fonction de la part des ménages le détendant.
Ce polygone sera constitué des 11 points de coordonnées $(x_i;y_i)$.
Le polygone $P$ ainsi tracé s'appelle "courbe de Lorenz".
On tracera sur le même graphique la droite $d$ d'équation $y=x$. - Soit $a$ l'aire du domaine délimité par $P$, l'axe des abscisses et la droite d'équation $x=100$.
Soit $s$ l'aire du domaine fermé délimité par $d$ et $P$.
Soit $t$ l'aire du triangle délimité par $d$, l'axe des abscisses et la droite d'équation $x=100$.
Le quotient ${s}/{t}$ s'appelle "indice de Gini" du patrimoine en France début 2018.
a. Calculer $t$.
b. Calculer $s$ à l'aide du tableur.
Pour trouver $a$, il est conseillé de décomposer le domaine concerné en un triangle rectangle et 9 trapèzes.
c. Donner une valeur approchée de l'indice de Gini du patrimoine en France début 2018 (arrondie à 0,001). - Retrouvons une estimation de cet indice par une méthode différente.
On considère la courbe $C$ donnant la part du patrimoine brut total en fonction de la part des ménages le détendant. Cette courbe passe évidemment par les 11 points du polygone $P$.
On admet qu'une approximation correcte de cette courbe est donnée par la représentation graphique $\C_f$ de la fonction $f(x)=10^{-6}x^4$
Cela se confirme graphiquement par le graphique suivant.
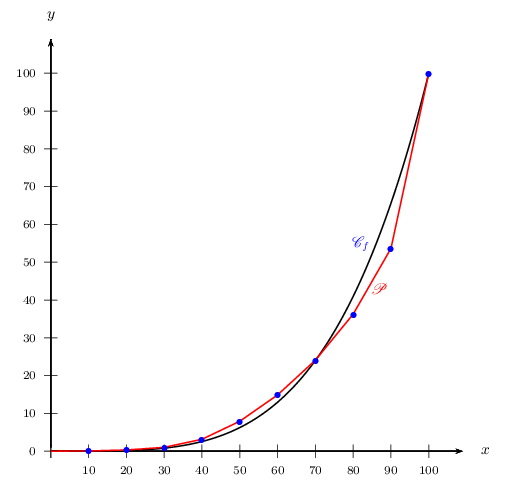
a. Calculer $A=∫_{0}^{100} f(x)dx$.
b. En déduire une nouvelle approximation de l'indice de Gini du patrimoine en France début 2018 (arrondie à 0,001). - L'indice de Gini du patrimoine en France a peu évolué entre 2014 et 2018.
En 2014, il était de 0,676.
A la même époque, l'indice de Gini du patrimoine en Allemagne était de 0,762, alors que l'indice de Gini du patrimoine en Slovénie était de 0,628.
Qu'en déduire concernant la France, l'Allemagne et la Slovénie en 2014? - Pour finir, étudions rapidement un autre coefficient mesurant les inégalités de richesse: l'indice de Palma.
Intéressons-nous au revenu des ménages (et non plus au patrimoine).
L’indice de Palma est la somme des revenus gagnés par les ménages situés dans le décile supérieur (le 10 % supérieur) divisée par la somme des revenus acquis par les 40 % des ménages au bas de l’échelle.
Voyons l'intérêt de cet indice sur un exemple. Les coefficients de Gini des revenus en 2014 au Honduras et au Maroc sont respectivement de 0,57 et 0,41.
La classe moyenne (comprise entre les 40 et 90 centiles) perçoit environ 50 % du revenu national au Honduras et au Maroc, mais l’indice de Palma est fort différent dans les deux pays, soit 5,21 au Honduras et 1,96 au Maroc.
Qu'en conclure?
Corrigé
- Les largeurs des classes étant identiques, la part du patrimoine attribuée à chaque classe est proportionnelle au patrimoine moyen de la classe.
Voici alors le tableau donnant la part du patrimoine français en fonction de la tranche de la population.

- Voici le tableau donnant les fréquences cumulées croissantes associées au tableau précédent.

Les $x_i$ donnent les fréquences cumulées de la population (en %)
Les $y_i$ donnent les fréquences cumulées du patrimoine (en %)
- Toutes les valeurs qui suivent sont données en pourcentages; par exemple, le nombre 100 correspond à 100%.
Contrairement à ce qui se fait dans cet exercice, certains ouvrages ne manipulent que des nombres entre 0 et 1, ce qui est parfaitement légitime étant donné que 100% vaut 1.
Voici le polygone $P$ donnant la part du patrimoine brut total en fonction de la part des ménages le détendant et la droite $d$ d'équation $y=x$.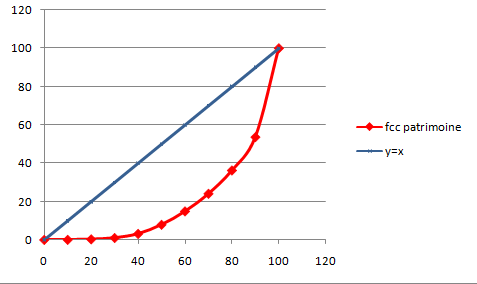
Pour information, il suffit de reporter dans le tableur la série concernée comme ci-dessous.
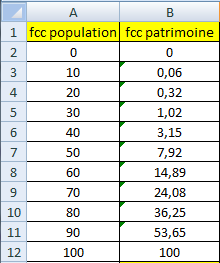
On sélectionne alors la série, puis on clique sur Insérer - Nuage de points - Nuage de points avec courbes lissées et marqueurs
Pour tracer la courbe $y=x$, on clique-droit sur la zone du graphique, puis on clique sur Sélectionner des données - Ajouter,
et on sélectionne la série des $x_i$ pour les abscisses comme pour les ordonnées. - Comme les abscisses et les ordonnées sont données en pourcentages, les aires réelles sont données en 10 millièmes; par exemple, le nombre 5000 correspond à une aire de 0,5.
a. Calculons $t$.
$t$ est l'aire du triangle démité par $d$, l'axe des abscisses et la droite d'équation $x=100$.
Ce triangle rectangle a pour aire: ${b ×h}/{2}={100 ×100}/{2}=5000$.
Donc $t=5\,000$
b. Calculons $a$.
On décompose le domaine concerné (hachuré en rouge) en un triangle rectangle et 9 trapèzes selon le dessin suivant.
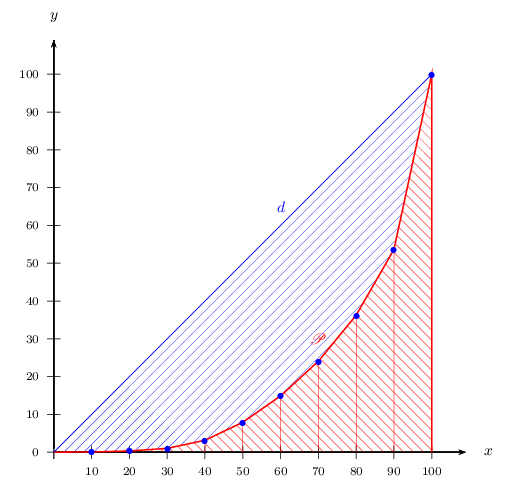
On reporte la formule =10*(B2+B3)/2 dans la cellule C3, et l'on tire la poignée de recopie vers le bas jusqu'à la cellule C12.
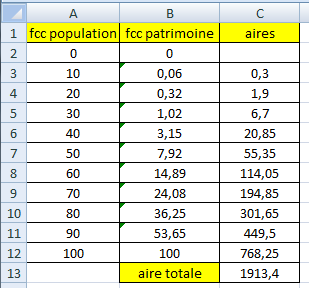
La cellule C13 contient la formule =SOMME(C3:C12) qui donne la somme des aires cherchée.
On a donc: $a≈1\,913,4$
Calculons $s$, aire du domaine hachuré en bleu.
On a clairement: $s=t-a$, et on obtient donc: $s≈5\,000-1\,913,4$
Soit: $s≈3\,086,6$
c. On a alors: ${s}/{t}≈{3\,086,6}/{5\,000}≈0,617$
L'indice de Gini du patrimoine en France début 2018 vaut environ 0,617.
- a. On calcule:
$A=∫_{0}^{100} f(x)dx=\[10^{-6}{x^5}/{5}\]_0^{100}$.
$A=10^{-6}{100^5}/{5}-10^{-6}{0^5}/{5}$.
$A=2\,000$.
b. $f$ étant continue et positive sur [0;100], $A$ correspond à l'aire du domaine situé sous la courbe.
On calcule alors: ${t-A}/{t}=0,6$
Une nouvelle approximation de l'indice de Gini du patrimoine en France début 2018 est donc 0,6. - L'indice de Gini du patrimoine en France était de 0,676 en 2014.
A la même époque, l'indice de Gini du patrimoine en Allemagne était de 0,762, alors que l'indice de Gini du patrimoine en Slovénie était de 0,628.
Or, plus l’indice de Gini est proche de zéro, plus on s’approche de l’égalité (tous les individus ont la même part du revenu). Plus il est proche de un, plus on est proche de l’inégalité absolue (un seul individu reçoit tous les revenus).
Donc, en 2014, les inégalités concernant le patrimoine étaient supérieures en Allemagne qu'en France, et supérieures en France qu'en Slovénie. - Les coefficients de Gini des revenus en 2014 au Honduras et au Maroc sont respectivement de 0,57 et 0,41. Ils sont donc assez proches, et par là, la répartition des revenus semble aussi inégalitaire dans les deux pays, quoique un peu plus inégalitaire au Honduras qu'au Maroc.
En tout cas, l'inégalité est pire en France car le coefficient de Gini y est encore supérieur.
Comme la classe moyenne (comprise entre les 40 et 90 centiles) perçoit environ 50 % du revenu national au Honduras et au Maroc, l'inégalité des revenus ne la concerne pas.
Mais l’indice de Palma est du Honduras (5,21) est très supérieur à celui du Maroc (1,96).
Le Honduras est donc une société beaucoup plus inégalitaire que le Maroc.
L’indice de Palma permet d’interpréter cette inégalité (concentration plus élevée des revenus au sommet) et il sera ainsi plus facile de proposer des politiques correctives.