Corrigé

Clique ICI pour revoir le cours sur les nombres premiers.

1. On a: $√{953}≈30,87$.
   Or les nombres premiers inférieur ou égal à $√{953}$ sont: 2, 3, 5, 7, 11, 13, 17, 19, 23 et 29.
   Et 953 n'est divisible par aucun d'eux (obtenu à l'aide de la calculatrice).
   Donc 953 est premier.


2. On cherche la décomposition de 117 en produit de facteurs premiers.
   On obtient: $117=3×39=3×3×13$
   
   Par conséquent, les diviseurs de 117 sont de la forme $3^a×13^b$
   où $0≤a ≤ 2$ et $0≤b ≤ 1$ .
   On peut éventuellement dresser l'arbre de dénombrement suivant.
   
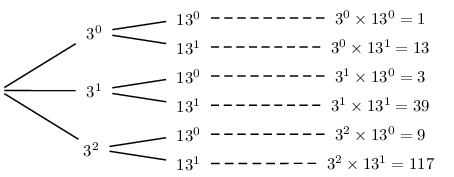
   L'ensemble des diviseurs de 117 est donc:
   $S=\{1, 3, 9, 13, 39, 117\}$


3. On obtient facilement: $124\,740=2^2×3^4×5×7×11$ et $17\,550=2×3^3×5^2×13$
   Et par là: $PGCD(124\,740;17\,550)=$2×3^3×5=270$


4. D'après le petit théorème de Fermat, comme $19$ est un nombre premier qui ne divise pas $24$, alors $24^{19-1}≡ 1 [19]$
   Soit: $24^{18}≡ 1 [19]$
   Et donc: $(24^{18})^{22}≡ 1^{22} [19]$, soit: $24^{396}≡ 1 [19]$
   
   D'après le petit théorème de Fermat, comme $23$ est un nombre premier qui ne divise pas $24$, alors $24^{23-1}≡ 1 [23]$
   Soit: $24^{22}≡ 1 [23]$
   Et donc: $(24^{22})^{18}≡ 1^{18} [23]$, soit: $24^{396}≡ 1 [23]$
   
   Par conséquent, il existe deux entiers $k$ et $k'$ tels que: $24^{396}=19k+1$ et $24^{396}=23k'+1$
   On en déduit que: $19k=23k'$.
   Donc 19 divise $23k'$.
   Et comme 19 et 23 sont premiers entre eux (car premiers), on en déduit que 19 divise k', et par là: $k'=19k"$, où $k"$ est un entier naturel.
   On obtient alors: $19k=23×19k"$, et donc: $k=23k"$.
   Finalement, on obtient $24^{396}=19×23k"+1$, soit: $24^{396}=437k"+1$, avec $k"$ entier naturel.
   Et comme on a évidemment $0≤1 < 437$, on obtient: $24^{396}≡1 [437]$