Corrigé

Une figure convenable.

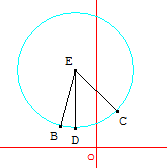
1. Clique ICI pour revoir le cours sur l'affixe d'un vecteur.
${EB}↖{→}$ a pour affixe: $z_{{EB}↖{→}}=z_B-z_E=-√{3}+i+1-(2+√{3})i=-√{3}+1+(-1-√{3})i$
${EC}↖{→}$ a pour affixe: $z_{{EC}↖{→}}=z_C-z_E=1+i√{3}+1-(2+√{3})i=2+(-2)i=2-2i$
${ED}↖{→}$ a pour affixe: $z_{{ED}↖{→}}=z_D-z_E=-1+(2+√{3}-2√{2})i+1-(2+√{3})i=-2√{2}i$

2. Clique ICI pour revoir le cours sur le module d'un complexe.
On a: $z_{{EB}↖{→}}=-√{3}+1+(-1-√{3})i$
D'où: $EB^2=(-√{3}+1)^2+(-1-√{3})^2=3-2√{3}+1+1+3+2√{3}+1=8$.

On a: $z_{{EC}↖{→}}=2+(-2)i$
D'où: $EC^2=2^2+(-2)^2=8$.

On a: $z_{{ED}↖{→}}=-2√{2}i$
D'où: $ED^2=0^2+(-2√{2})^2=8$.

Finalement: $EB^2=EC^2=ED^2$, et par là les 3 distances (positives) EB, EC et ED sont égales.
Donc B, C et D appartiennent à un même cercle de centre E (de rayon $√8$).

3.a. Supposons que M a pour affixe $z_E+√{8}e^{iθ}$, où $θ$ est un réel quelconque.
Donc: $zM-z_E=√{8}e^{iθ}$, et donc: $|zM-z_E|=√{8}$.
Et par là: $EM=√{8}$, et donc M est sur $\C_E$.
3.b. Supposons que M est sur $\C_E$. Donc $EM=√{8}$
Et par là: $|zM-z_E|=√{8}$, et par conséquent, il existe un réel $θ$ tel que $zM-z_E=√{8}e^{iθ}M$.
Donc: $z_M=z_E+√{8}e^{iθ}$.
M a bien pour affixe $z_E+√{8}e^{iθ}$.
3.c. Si M est en C, alors $z_{{EM}↖{→}}=z_{{EC}↖{→}}$.
Or $z_{{EC}↖{→}}=2-2i=√{8}({√{2}}/{2}-{√{2}}/{2}i)=√{8}(\cos (-{π}/{4})+\sin (-{π}/{4})i)$
Et par là $θ=-{π}/{4}$ convient.

4. On détermine $\arg {z_D-z_E}/{z_C-z_E}$.
On calcule donc: ${z_D-z_E}/{z_C-z_E}={-2√{2}i}/{2-2i}={(-2√{2}i)×(2+2i)}/{(2-2i)×(2+2i)}$
Soit: ${z_D-z_E}/{z_C-z_E}={-4√{2}i+4√{2}}/{8}={-{√{2}}/{2}i+{√{2}}/{2}=\cos (-{π}/{4})+\sin (-{π}/{4})i$
Donc une mesure de l'angle $({EC}↖{→};{ED}↖{→})$ est $-{π}/{4}$.