 Nombres complexes
Nombres complexes
A SAVOIR: le cours sur les complexes
Exercice 3
Les 2 parties sont indépendantes.
Partie A
Déterminons (sans calculatrice) la forme algébrique de $z=i(1-2i)^5$.
Partie B
Dans le plan complexe muni du repère (O,I,J), on considère le point A d’affixe
$a={√3}/{2}+{1}/{2}i$
1. Déterminer l'affixe du milieu K de $[AJ]$. La présenter sous forme trigonométrique.
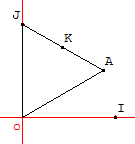
Faire une figure.
2. Déterminer la distance OA.
3. Déterminer une mesure (en radians) de l'angle orienté $({OI}↖{→};{OA}↖{→})$
4. Montrer, sans calcul, que $AK=0,5$
Solution...
Corrigé
Partie A
On utilise la formule du binôme.
On écrit: $(1-2i)^5=∑↙{k=0}↖5 (\table 5;k)1^{5-k}×(-2i)^k$
Soit: $(1-2i)^5=1^5+(\table 5;1)1^4×(-2i)+(\table 5;2)1^3×(-2i)^2+(\table 5;3)1^2×(-2i)^3+(\table 5;3)1×(-2i)^4+(-2i)^5$
Soit: $(1-2i)^5=1+5×1×(-2i)+10×1×(4i^2)+10×1×(-8i^3)+5×1×(16i^4)+(-32i^5)$
Soit: $(1-2i)^5=1-10i-40+80i+80-32i$
Soit: $(1-2i)^5=41+38i$
Et par là: $z=i(41+38i)$
Soit: $z=-38+41i$
C'est la forme algébrique demandée.
Partie B
1. Le milieu K du segment $[AJ]$ a pour affixe $z_K={z_A+z_J}/{2}={{√3}/{2}+{1}/{2}i+i}/{2}$
Soit: $z_K={√3}/{4}+{3}/{4}i$
$|z_K|=√{{3}/{16}+{9}/{16}}=√{{12}/{16}}={√{3}}/{2}$
On factorise: $z_K={√{3}}/{2}({1}/{2}+i{√{3}}/{2})$.
On note alors que: $z_K={√{3}}/{2}(\cos ({π}/{3})+i\sin ({π}/{3}))$.
C'est l'écriture de $z_K$ sous forme trigonométrique.
2. $OA=|z_A|=√{{3}/{4}+{1}/{4}}=1$
La distance OA vaut 1.
3. On factorise naïvement: $z_A={1({√3}/{2}+{1}/{2}i)$.
On note alors que: $z_A=1(\cos ({π}/{6})+i\sin ({π}/{6}))$.
C'est l'écriture de $z_A$ sous forme trigonométrique.
Par conséquent: $\arg z_A={π}/{6}\, [2 π]$.
Une mesure (en radians)
de l'angle orienté $({OI}↖{→};{OA}↖{→})$ est donc ${π}/{6}$
4. On sait qu'une mesure (en radians)
de l'angle orienté $({OI}↖{→};{OJ}↖{→})$ est ${π}/{2}$
Donc, par différence, une mesure (en radians)
de l'angle orienté $({OA}↖{→};{OJ}↖{→})$ est ${π}/{2}-{π}/{6}={π}/{3}$
Par ailleurs, on sait que OJ=1, et on a vu que OA=1.
Par conséquent, le triangle OAJ possède un angle de mesure ${π}/{3}$, et les côtés correspondant sont égaux. Donc il est équilatéral.
Et donc AJ=1.
Et par là, comme K est le milieu de [AJ], on en déduit que $AK=0,5$