Nombres complexes
Nombres complexes
A SAVOIR: le cours sur les complexes
Exercice 4
Un exercice assez simple qui allie complexes et géométrie.
Dans le plan complexe muni du repère (O,I,J), on considère les points A, B, et C d’affixes respectives
$a=2+2i$ $b=-√{3}+i$
$c=1+i√{3}$
1. Déterminer les affixes des vecteurs ${AB}↖{→}$, ${AC}↖{→}$.
2. Les points A, B et C sont-ils alignés?
3. Déterminer l'affixe du milieu K de [OA].
4. OBAE est un parallélogramme. Quelle est l'affixe de E?
5. Montrer que K est le milieu de [BE]
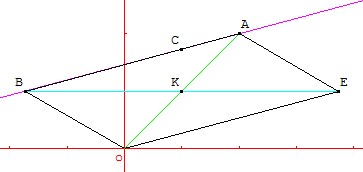
6. Faire une figure.
Solution...
Corrigé
1. Clique ICI pour revoir le cours sur l'affixe d'un vecteur.
${AB}↖{→}$ a pour affixe: $z_{{AB}↖{→}}=z_B-z_A=-√{3}+i-2-2i=-√{3}-2-i$
${AC}↖{→}$ a pour affixe: $z_{{AC}↖{→}}=z_C-z_A=1+i√{3}-2-2i=-1-(2-√{3})i$
2. On a: $z_{{AC}↖{→}}=-1-(2-√{3})i$ et $z_{{AB}↖{→}}=-√{3}-2-i$.
Donc, d'après le 1., on obtient: $(√{3}+2)z_{{AC}↖{→}}=z_{{AB}↖{→}}$
Donc: $(√{3}+2){AC}↖{→}={AB}↖{→}$.
Par conséquent, les vecteurs ${AB}↖{→}$ et ${AC}↖{→}$ étant colinéaires,
les points A, B et C sont alignés.
3. K est le milieu de [OA].
Donc $z_K={z_O+z_A}/{2}={0+2+2i}/{2}=$$1+i$.
4. OBAE est un parallélogramme$⇔{AB}↖{→}={EO}↖{→}⇔z_{{AB}↖{→}}=z_{{EO}↖{→}}$
OBAE est un parallélogramme$⇔-√{3}-2-i=0-z_E⇔z_E=$$√{3}+2+i$
5. OBAE est un parallélogramme et K est le milieu de [OA].
Donc K est le milieu de [BE].
6. Une figure convenable.