Corrigé

Partie A
$\mathit{f}\prime \left(\mathit{x}\right)=\frac{-\left(-1\right)}{{\left(1-\mathit{x}\right)}^2}=\frac{1}{{\left(\mathit{x}-1\right)}^2}$.
Le dénominateur est un carré, il reste donc positif, et par là, $\mathit{f}\prime \left(\mathit{x}\right)$ également.
Donc $\mathit{f}$ est strictement croissante sur l'intervalle $]-\mathit{\infty };1[$ et sur l'intervalle $]1;+\mathit{\infty }[$.
Comme $\underset{\mathit{x}\to +\mathit{\infty }}{\lim }1-\mathit{x}=-\mathit{\infty }$, on obtient $\underset{\mathit{x}\to +\mathit{\infty }}{\lim }\mathit{f}\left(\mathit{x}\right)=0$
De même, on obtient $\underset{\mathit{x}\to -\mathit{\infty }}{\lim }\mathit{f}\left(\mathit{x}\right)=0$
Comme $"1\}\}1-x=0">\underset{{}_{\mathit{x}\text{>}1}^{\mathit{x}\to 1}}{\lim }1-\mathit{x}=0$ et comme lorsque $"1">\mathit{x}\text{>}1$, on obtient $"1\}\}f(x)=-\infty ">\underset{{}_{\mathit{x}\text{>}1}^{\mathit{x}\to 1}}{\lim }\mathit{f}\left(\mathit{x}\right)=-\mathit{\infty }$.
De même, on obtient .
D'où le tableau de variation de $\mathit{f}$:

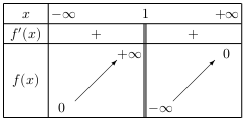
Il est alors clair que les valeurs prises par $\mathit{f}\left(\mathit{x}\right)$ lorsque $\mathit{x}$ décrit $]-\mathit{\infty };1[\cup ]1;+\mathit{\infty }[$ sont tous les réels excepté 0.

Partie B
Remarquons tout d'abord que, comme $\frac{1}{\mathit{z}}$ intervient dans l'expression, $\mathit{z}$ est nécessairement non nul
Par ailleurs, un imaginaire pur s'écrit sous la forme $\mathit{k}\mathit{i}$, avec $\mathit{k}$ réel.
Donc: $\mathit{i}+\frac{1}{\mathit{z}}$ est imaginaire pur si et seulement si il existe un réel $\mathit{k}$ tel que $\mathit{i}+\frac{1}{\mathit{z}}=\mathit{k}\mathit{i}$      (1)
(1) $\iff$ $\frac{1}{\mathit{z}}=\left(\mathit{k}-1\right)\mathit{i}$
Notons ici que $\mathit{k}$ est différent de 1, sinon on obtiendrait $\frac{1}{\mathit{z}}=0$, ce qui est impossible.
(1) $\iff$ $\mathit{z}=\frac{1}{\left(\mathit{k}-1\right)\mathit{i}}$
(1) $\iff$ $\mathit{z}=\frac{\mathit{i}}{\left(\mathit{k}-1\right){\mathit{i}}^2}=\frac{1}{1-\mathit{k}}\mathit{i}$
Donc finalement, $\mathit{i}+\frac{1}{\mathit{z}}$ est imaginaire pur si et seulement si $\mathit{z}$ s'écrit sous la forme $\mathit{z}=\mathit{f}\left(\mathit{k}\right)\mathit{i}$, avec $\mathit{f}\left(\mathit{k}\right)=\frac{1}{1-\mathit{k}}$.
Or $\mathit{k}$ peut prendre toutes les valeurs de l'ensemble $]-\mathit{\infty };1[\cup ]1;+\mathit{\infty }[$.
Donc, d'après la partie A, le nombre complexe $\mathit{z}$ s'écrit sous la forme $\mathit{z}=\mathit{m}\mathit{i}$, où $\mathit{m}$ décrit tous les réels excepté 0.
Donc l'ensemble cherché est l'axe des ordonnées privé de l'origine.