 Nombres complexes
Nombres complexes
A SAVOIR: le cours sur les complexes
Exercice 9
Un exercice classique qui allie géométrie et complexes.
Le plan complexe est muni d'un repère orthonormé direct.
On considère le point A d'affixe 1 et le point B d'affixe $i$.
A tout point M d'affixe $z_M=x+iy$, avec $x$ et $y$ deux réels tels que $y≠0$, on associe le point M' d'affixe $z_{M'}=-iz_M$.
On désigne par I le milieu du segment [AM].
Le but de l'exercice est de montrer que pour tout point M n'appartenant pas à (OA),
la médiane (OI) du triangle OAM est aussi une hauteur du triangle OBM' (propriété 1)
et que BM'=2OI (propriété 2).
1. Dans cette question 1. et uniquement dans cette question 1., on prend $z_M=2e^{-i{π}/{3}}$.
a. Déterminer la forme algébrique de $z_M$.
b. Montrer que $z_{M'}=-√3-i$. Déterminer le module et un argument de $z_{M'}$.
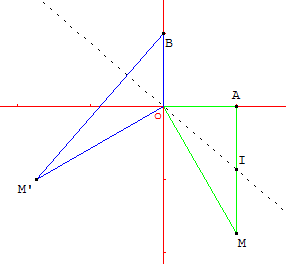
c. Placer les points A, B, M, M' et I dans le repère $(O,u↖{→} ,v↖{→} )$.
Tracer la droite (OI) et vérifier rapidement les propriétés 1 et 2 à l'aide du graphique.
2. On revient au cas général en prenant avec $z_M=x+iy$, avec $x$ et $y$ deux réels tels que $y≠0$.
a. Déterminer l'affixe du point I en fonction de $x$ et $y$.
b. Déterminer l'affixe du point M' en fonction de $x$ et $y$.
c. Ecrire les coordonnées des points I, B et M'.
d. Montrer que la droite (OI) est une hauteur du triangle OBM'.
e. Montrer que BM'=2OI.
Solution...
Corrigé
1.a. $z_M=2e^{-i{π}/{3}}=2(\cos(-{π}/{3})+i\sin(-{π}/{3}))=2({1}/{2}-i{√3}/{2})$.
Soit: $z_M=1-i√3$.
1.b. $z_{M'}=-iz_M=-i(1-i√3)=-i+i^2√3$
Soit: $z_{M'}=-√3-i$.
Clique ICI pour revoir le cours sur module et argument.
$|z_{M'}|=√{(-√3)^2+(-1)^2}=√{3+1}=√{4}=2$. Soit: $|z_{M'}|=2$.
On factorise: $z_{M'}=2({-√3}/{2}-i{1}/{2})$.
On note alors que: $z_{M'}=2(\cos (-{5π}/{6})+i\sin (-{5π}/{6}))$.
C'est l'écriture de $z_{M'}$ sous forme trigonométrique.
Par conséquent: $\arg z_{M'}=-{5π}/{6}\, [2 π]$.
$-{5π}/{6}$ est un argument de $z_{M'}$.
1.c. Les propriétés 1 et 2 se vérifient sur le graphique ci-dessous.
2.a. Clique ICI pour revoir le cours sur l'affixe d'un milieu .
I le milieu du segment [AM],
donc $z_I={z_A+z_M}/{2}={1+x+iy}/{2}$.
Soit: $z_I={1+x}/{2}+i{y}/{2}$
2.b. $z_{M'}=-iz_M=-i(x+iy)=-ix-i^2y$.
Soit: $z_{M'}=y-ix\,$
2.c.
On obtient les coordonnées des points à partir de leurs affixes.
Ainsi: $I({1+x}/{2};{y}/{2})$ $B(0;1)$ $M'(y;-x)$.
2.d.
On a: ${OI}↖{→}({1+x}/{2};{y}/{2})$ et ${BM'}↖{→}(y;-x-1)$
Le repère étant orthonormé, nous calculons le produit scalaire ${OI}↖{→}.{BM'}↖{→}$ de la façon suivante:
${OI}↖{→}.{BM'}↖{→}={1+x}/{2}×y+{y}/{2}×(-x-1)={y/{2}+{xy}/{2}-{xy}/{2}-{y}/{2}=0$
On a donc ${OI}↖{→}.{BM'}↖{→}=0$, et par là, les vecteurs ${OI}↖{→}$ et ${BM'}↖{→}$ sont orthogonaux,
Les droites (OI) et (BM') sont donc perpendiculaires.
Ce qui montre que (OI) est la hauteur du triangle OBM' issue de O.
2.e. Le repère étant orthonormé, nous calculons les distances BM' et OI de la façon suivante:
$BM'=√{y^2+(-x-1)^2}=√{x^2+2x+y^2+1}$
$OI=√{({1+x}/{2})^2+({y}/{2})^2}=√{{1+2x+x^2+y^2}/{4}}={1}/{2}√{x^2+2x+y^2+1}$
On constate alors que BM'=2OI. c.q.f.d. (ce qu'il fallait démontrer)