 Graphes et matrices
Graphes et matrices
A SAVOIR: le cours sur les graphes et les matrices
Exercice 2
Le plan est muni d'un repère orthonormé (O,A,C).
Les coordonnées d'un point ou d'un vecteur peuvent alors s'écrire sous forme:
d'un couple $(x;y)$, ou d'une matrice ligne $(\table x,y)$, ou d'une matrice colonne $(\table x;y)$.
Dans cet exercice, nous adopterons l'écriture en matrice colonne.
1. On considère la translation $t_{u↖{→}}$ de vecteur $u↖{→}(\table 2;3)$.
L'image d'un point $M(\table x;y)$ par $t_{u↖{→}}$ est un point $M'(\table x';y')$ défini par: $MM'↖{→}=u↖{→}$.
Exprimer la matrice $(\table x';y')$ en fonction des matrices $(\table x;y)$ et $(\table 2;3)$.
2. On considère la symétrie axiale par rapport à l'axe des abscissses, que l'on note $s_{ox}$.
L'image d'un point $M(\table x;y)$ par $s_{ox}$ est un point $M'(\table x';y')$ défini par $(\table x';y')=(\table x;-y)$.
Donner une matrice $S$ d'ordre 2, définie par $S=(\table a,b;c,d)$, telle que: $(\table x';y')=S×(\table x;y)$.
3. On considère la transformation du plan, notée $r$, telle que:
l'image de tout point $M(\table x;y)$ par $r$ est un point $M'(\table x';y')$ défini par $(\table x';y')=R×(\table x;y)$,
où $R$ est la matrice d'ordre 2 définie par: $R=(\table 0.5,-{√{3}}/{2};{√{3}}/{2},0.5)$.
Déterminer les images des points $O(\table 0;0)$, $A(\table 1;0)$, $B(\table 1;1)$ et $C(\table 0;1)$.
Placer tous les points sur un graphique.
Conjecturer la nature de la transformation $r$.
4. On considère l' homothétie de centre 0 de rapport 2, que l'on note $h$.
L'image d'un point $M(\table x;y)$ par $h$ est un point $M'(\table x';y')$ défini par $OM'↖{→}=2 OM↖{→}$.
Donner une matrice $H$ d'ordre 2, définie par $H=(\table a,b;c,d)$, telle que: $(\table x';y')=H×(\table x;y)$.
Corrigé
1. On a: $MM'↖{→}=u↖{→}$.
Donc: $\{\table x'-x=2;y'-y=3$
Et donc: $\{\table x'=x+2;y'=y+3$
Et par là: $(\table x';y')=(\table x;y)+(\table 2;3)$
2. On a: $(\table x';y')=(\table x;-y)$.
On constate que: $\{\table x'=1×x+0×y;y'=0×x-1×y$
On propose alors: $S=(\table 1,0;0,-1)$
On a bien: $(\table x';y')=S×(\table x;y)$.
La matrice S convient.
3. On a: $(\table x';y')=(\table 0.5,-{√{3}}/{2};{√{3}}/{2},0.5)×(\table x;y)$
A la calculatrice (ou de tête), on obtient: $0'(\table 0;0)$ $A'(\table 0.5;{√{3}}/{2})$ $B'(\table 0.5-{√{3}}/{2};{√{3}}/{2}+0.5)$
$C'(\table -{√{3}}/{2},0.5)$
Voici un graphique convenable.
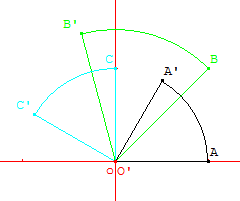
On conjecture que la transformation $r$ est la rotation de centre O et d'angle 60° dans le sens "de A vers C".
4. On a: $OM'↖{→}=2 OM↖{→}$.
Donc: $\{\table x'=2×x;y'=2×y$
On constate que: $\{\table x'=2×x+0×y;y'=0×x+2×y$
On propose alors: $H=(\table 2,0;0,2)$
On a bien: $(\table x';y')=H×(\table x;y)$.
La matrice H convient.