Graphes et matrices
Graphes et matrices
A SAVOIR: le cours sur les graphes et les matrices
Exercice 3
Le plan est muni d'un repère orthonormé.
1. La parabole $P$ représentant le trinôme du second degré $f$ passe par les points $E(-2;-9)$, $F(1;6)$ et $G(4;3)$.
Déterminer l'expression donnant $f(x)$.
2. Déterminer les valeurs de $a$, $b$, $c$ et $d$ tellles que la courbe $\C$ représentant le polynome du 3ème degré $g$, donné par l'expression $g(x)=ax^3+bx^2+cx+d$, passe par les points E, F et G
et admmette une tangente $t$ de coefficient directeur 2 au point 5.
Déterminer l'équation réduite de $t$.
3. Représenter $P$, $\C$ et $t$, et vérifier graphiquement vos résultats.
Solution...Corrigé
1. Le trinôme du second degré $f$ admet une expression du type: $f(x)=ax^2+bx+c$ (avec $a$ non nul).
La parabole $P$ passe par E, F et G $⇔$ $\{\table f(-2)=-9;f(1)=6;f(4)=3$ (S)
(S) $⇔$ $\{\table 4a-2b+c=-9;a+b+c=6;16a+4b+c=3$
(S) $⇔$ $A×X=B$ avec
$A=(\table 4,-2,1;1,1,1;16,4,1)$ $X=(\table a;b;c)$ et $B=(\table -9;6;3)$
A l'aide de la calculatrice, on constate que A est inversible et que $A^{-1}=(\table {1}/{18},-{1}/{9},{1}/{18};-{5}/{18},{2}/{9},{1}/{18};{2}/{9},{8}/{9},-{1}/{9})$.
On a donc: (S) $⇔$ $X=A^{-1}×B$
A l'aide de la calculatrice, on obtient alors: (S) $⇔$ $X=(\table -1;4;3)$
Par conséquent: $f(x)=-x^2+4x+3$
2. On procède comme ci-dessus.
La courbe $\C$ passe par E, F et G et elle admmet une tangente de coefficient directeur 2 au point 5
si et seulement si $\{\table g(-2)=-9;g(1)=6;g(4)=3;g'(5)=2$ (S)
On note alors que, comme $g(x)=ax^3+bx^2+cx+d$, on a: $g'(x)=3ax^2+2bx+c$.
(S) $⇔$ $\{\table -8a+4b-2c+d=-9;a+b+c+d=6;64a+16b+4c+d=3;75a+10b+c=2$
(S) $⇔$ $A×X=B$ avec
$A=(\table -8,4,-2,1;1,1,1,1;64,16,4,1;75,10,1,0)$ $X=(\table a;b;c;d)$ et $B=(\table -9;6;3;2)$
A l'aide de la calculatrice, on constate que A est inversible
et que $A^{-1}=(\table -{5}/{702},{8}/{351},-{11}/{702},{1}/{39};{1}/{13},-{7}/{39},{4}/{39},-{1}/{13};-{55}/{234},{10}/{117},{35}/{234},-{2}/{13};{58}/{351},{376}/{351},-{83}/{351},{8}/{39})$.
On a donc: (S) $⇔$ $X=A^{-1}×B$
A l'aide de la calculatrice, on obtient alors: (S) $⇔$ $X=(\table {8}/{39};-{21}/{13};{36}/{13};{181}/{39})$
Par conséquent: $g(x)={8}/{39}x^3-{21}/{13}x^2+{36}/{13}x+{181}/{39}$
Déterminons l'équation réduite de $t$, tangente à $\C$ en 5.
Comme $g'(5)=2$, $t$ a une équation du type $y=2x+p$.
Or, $g(5)={8}/{39}×5^3-{21}/{13}×5^2+{36}/{13}×5+{181}/{39}={146}/{39}$
Et donc: $2×5+p={146}/{39}$.
Et par là: $p=-{244}/{39}$
Donc $t$ a pour équation réduite: $y=2x-{244}/{39}$
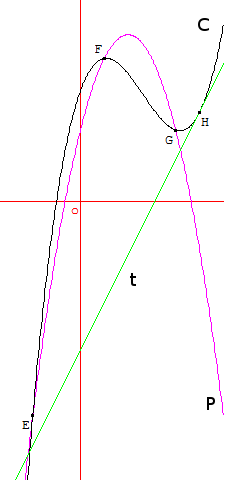
3. $P$, $\C$ et $t$ sont représentées ci-dessous.
Nous constatons graphiquement que les deux courbes passent bien par E, F et G; et la courbe $\C$ admet bien la droite $t$ comme tangente en 5.
Le point de tangence H a pour coordonnées $(5;{146}/{39})$