 Graphes et matrices
Graphes et matrices
A SAVOIR: le cours sur les graphes et les matrices
Exercice 6
Dans un département, deux sociétés, notée A et B, se partagent le marché de l'entretien de photocopieurs. Les contrats d'entretien sont renouvelés chaque année.
En 2010, la société A a possédait $40%$ du marché.
Depuis, chaque année, la société A perd $2%$ de ses contrats au profit de la société B, alors que la société B perd $7%$ de ses contrats au profit de la société A.
On considère un photocopieur pris au hasard.
Soit $a_n$ la probabilité que ce photocopieur soit entretenu par la société A en l'année 2010+$n$.
Soit $b_n$ la probabilité que ce photocopieur soit entretenu par la société B en l'année 2010+$n$.
Soit $P_n=(\table a_n,b_n)$ l'état probabiliste en l'année 2010+$n$.
On a donc: $P_0=(\table 0.40,0.60)$
On note $X_n$ la société qui entretient ce photocopieur en l'année 2010+$n$.
- La suite $(X_n)$ définit une chaîne de Markov. Pourqoui?
- Donner la distribution initiale du système.
- Donner un arbre pondéré associé aux 2 premières transitions, et déterminer la distribution après ces 2 transitions.
- Donner le graphe probabiliste et la matrice de transition qui sont associés à la chaîne de Markov (les sommets étant pris dans l'odre alphabétique).
- Donner la matrice de la distribution initiale $π_0$.
Retrouver la distribution après 2 transitions par un calcul matriciel. - Déterminer la distribution du système pour l'année 2021 et interpréter le résultat.
- Déterminer la distribution invariante du système et interpréter le résultat.
Corrigé
- La suite $(X_n)$ définit une chaîne de Markov car, à chaque étape $n$ , les probabilités de transition d'un état à un autre ne dépendent pas de $n$.
-
La distribution initiale du système est la suivante:
$p(X_0=A)=0,40$ $p(X_0=B)=0,60$ - Voici un arbre pondéré associé aux 2 premières transitions.
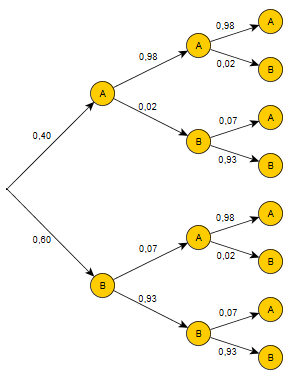
Déterminons la distribution après ces 2 transitions.
$\{A, B\}$ constitue une partition de l'univers. D'après la formule des probabilités totales, on obtient:
$p(X_2=A)=0,4×0,98×0,98+0,4×0,02×0,07+0,6×0,07×0,98+0,6×0,93×0,07=0,46494$
$p(X_2=B)=1-p(X_2=A)=0,53506$
-
Voici le graphe probabiliste et la matrice de transition demandés.
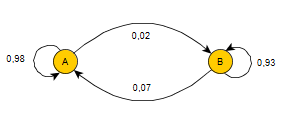
$P=(\table 0.98,0.02;0.07,0.93)$ - La distribution initiale du système est la suivante:
$p(X_0=A)=0,40$ $p(X_0=B)=0,60$
Donc: $π_0=(\table 0.40,0.60)$
On sait que: $π_{2}=π_0×P^2$
Or: $P=(\table 0.98,0.02;0.07,0.93)$
Donc on obtient (à la calculatrice): $π_2=(\table 0.46494,0.53506)$
On retrouve le fait que:
$p(X_2=A)=0,46494$ $p(X_2=B)=0,53506$ - On obtient (à la calculatrice): $π_{11}=π_0×P^{11}=(\table a,b)$
où $a$ vaut environ 0,64 et $b$ vaut environ 0,36.
En 2021 (pour $n=11$), la probabilité que le photocopieur soit entretenu par A vaut environ 0,64, et la probabilité que le photocopieur soit entretenu par B vaut environ 0,636. - On a: $P=(\table 0.98,0.02;0.07,0.93)$
On constate tout d'abord que la matrice de transition $P$ ne comporte pas de zéro.
Donc la suite $(π_n)$ converge vers une matrice de distribution $π$, unique solution de l'équation $π=π×P$.
Résolvons l'équation $π=π×P$.
On pose: $π=(\table a, b)$ avec $a+b=1$ (un détail à ne pas oublier!)
Par conséquent: $π=(\table a, 1-a)$
Donc: $π=π×P$ $ ⇔$ $\{\table a=a×0.98+(1-a)×0.07;1-a=a×0.02+(1-a)×0.93$
Soit: $π=π×P$ $ ⇔$ $\{\table a=0.98a+0.07-0.07a;1-a=0.02a+0.93-0.93a$
Soit: $π=π×P$ $ ⇔$ $\{\table 0.09a=0.07;-0.09a=-0.07$
Soit: $π=π×P$ $ ⇔$ $a={7}/{9}$
La solution unique de l'équation $π=π×P$ est $π=(\table {7}/{9},{2}/{9})$, qui est la distribution invariante du système.
La suite $(π_n)$ converge alors vers $π$, ce qui signifie que, lorsque $n$ tend vers $+\∞$, la probabilité que le photocopieur soit entretenu par l'entreprise A tend vers ${7}/{9}$ (environ 0,78), la probabilité que le photocopieur soit entretenu par l'entreprise B tend vers ${2}/{9}$ (environ 0,22).
A la longue, l'entreprise A domine le marché.