 Graphes et matrices
Graphes et matrices
A SAVOIR: le cours sur les graphes et les matrices
Exercice 7
Voici l'expérience (très simplifiée) des urnes d'Ehrenfest.
Deux urnes A et B sont vides. Au départ, 2 boules numérotées 0 et 1 sont placées dans l'urne A. L'urne B reste vide.
On répète alors les deux actions suivantes.
Un nombre $k$ est choisi aléatoirement et de façon équiprobable entre 0 et 1. La boule numérotée $k$ est changée d'urne.
Ces deux actions constituent une "étape" de l'expérience.
On note $X_n$ la variable aléatoire donnant le nombre de boules contenues dans l'urne A à l'issue de la n-ième étape
- Soit $n$ un naturel non nul et $i$ un entier pris dans $\{0,1,2\}$.
Montrer que $p_{X_n=i}(X_{n+1}=i)=0$
Montrer que $p_{X_n=2}(X_{n+1}=1)=1$
Montrer que $p_{X_n=0}(X_{n+1}=1)=1$ - Soit $n$ un naturel non nul et $i$ un entier pris dans $\{0,1,2\}$.
Déterminer $p_{X_n=2}(X_{n+1}=0)$ et $p_{X_n=0}(X_{n+1}=2)$ - Soit $n$ un naturel non nul et $i$ un entier pris dans $\{0,1,2\}$.
Déterminer $p_{X_n=1}(X_{n+1}=0)$
Déterminer $p_{X_n=1}(X_{n+1}=2)$
- La suite $(X_n)$ définit une chaîne de Markov. Pourquoi?
- Donner la distribution initiale du système et la matrice de la distribution initiale $π_0$.
- Donner le graphe probabiliste et la matrice de transition M qui sont associés à la chaîne de Markov (les sommets étant pris dans l'ordre alphabétique).
- On pose: $P=(\table 0.5,0,0.5;0,1,0;0.5,0,0.5)$
Soit $n$ un naturel non nul.
Montrer que:
si $n$ est impair, alors: $M^n=M$
si $n$ est pair, alors: $M^n=P$ - Déterminer la distribution du système après la n-ième étape et interpréter le résultat.
Corrigé
- A chaque étape, une boule change d'urne. Et comme il n'y a que 2 urnes, le nombre de boules de chaque urne change.
En particulier, si l'urne A contient $i$ boules après l'étape $n$, alors l'urne A ne contiendra plus $i$ boules après l'étape $n+1$. Par conséquent, $p_{X_n=i}(X_{n+1}=i)=0$.
Si l'urne A contient les $2$ boules après l'étape $n$, alors la boule choisie fait partie de ces 2 boules. Elle change alors d'urne. Et par là, l'urne A contient une seule boule après l'étape $n+1$.
Par conséquent, $p_{X_n=2}(X_{n+1}=1)=1$.
Si l'urne A ne contient aucune boule après l'étape $n$, alors la boule choisie est située dans l'urne B. Elle change alors d'urne. Et par là, l'urne A contient une seule boule après l'étape $n+1$.
Par conséquent, $p_{X_n=0}(X_{n+1}=1)=1$ - Comme $p_{X_n=2}(X_{n+1}=1)=1$, on en déduit que: $p_{X_n=2}(X_{n+1}=0)=0$
Comme $p_{X_n=0}(X_{n+1}=1)=1$, on en déduit que: $p_{X_n=0}(X_{n+1}=0)=0$ - Si l'urne A contient une boule après l'étape $n$, alors l'autre boule est dans l'urne B. Et la probabilité que la boule choisie soit celle située dans l'urne A vaut $0,5$.
Et par là, la probabilité que l'urne A soit vide après l'étape $n+1$ vaut $0,5$.
Par conséquent: $p_{X_n=1}(X_{n+1}=0)=0,5$.
Si l'urne A contient une boule après l'étape $n$, alors l'autre boule est dans l'urne B. Et la probabilité que la boule choisie soit celle située dans l'urne B vaut $0,5$.
Et par là, la probabilité que l'urne A contienne 2 boules après l'étape $n+1$ vaut $0,5$.
Par conséquent: $p_{X_n=1}(X_{n+1}=2)=0,5$. - La suite $(X_n)$ définit une chaîne de Markov car, à chaque étape $n$ , les probabilités de transition d'un état à un autre ne dépendent pas de $n$.
-
La distribution initiale du système est la suivante:
$p(X_0=0)=0$ $p(X_0=1)=0$ $p(X_0=2)=1$
La matrice de la distribution initiale est donc: $π_0=(\table 0,0,1)$ -
Voici le graphe probabiliste et la matrice de transition demandés.
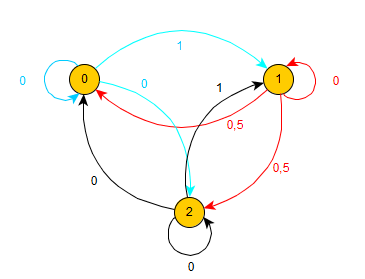
$M=(\table 0,1,0;0.5,0,0.5;0,1,0)$ - Montrons la propriété demandée par récurrence sur $n$.
Initialisation: pour $n=1$, la propriété est évidente car 1 est impair, et on a bien: $M^1=M$.
Hérédité: supposons la propriété vraie au rang $n$.
Nous allons démontrer qu'elle est vraie au rang $n+1$.
Premier cas: supposons que $n$ est impair.
On a alors: $M^n=M$.
Et comme $n+1$ est nécessairement pair, nous devons prouver que: $M^{n+1}=P$
On calcule donc: $M^{n+1}=M^n×M=M×M=(\table 0,1,0;0.5,0,0.5;0,1,0)^2$
A la calculatrice, on obtient: $M^{n+1}=(\table 0.5,0,0.5;0,1,0;0.5,0,0.5)$
Donc on a bien bien: $M^{n+1}=P$
Second cas: supposons que $n$ est pair.
On a alors: $M^n=P=(\table 0.5,0,0.5;0,1,0;0.5,0,0.5)$.
Et comme $n+1$ est nécessairement impair, nous devons prouver que: $M^{n+1}=M$
On calcule donc: $M^{n+1}=M^n×M=(\table 0.5,0,0.5;0,1,0;0.5,0,0.5)×(\table 0,1,0;0.5,0,0.5;0,1,0)$
A la calculatrice, on obtient: $M^{n+1}=(\table 0,1,0;0.5,0,0.5;0,1,0)$.
On a bien: $M^{n+1}=M$.
Finalement, on a montré que la propriété est vraie au rang $n+1$.
Conclusion: la propriété est vraie pour tout naturel $n$ non nul.
- On sait que: $π_{n}=π_0×M^{n}$
Donc, si $n$ est impair: $π_{n}=π_0×M=(\table 0,1,0)$
Et si $n$ est pair, $π_{n}=π_0×P=(\table 0.5,0,0.5)$
Interprétation.
Si $n$ est impair, alors, après $n$ étapes, l'urne A contient nécessairement 1 boule.
Si $n$ est pair, alors, après $n$ étapes, soit l'urne A est vide, soit elle contient 2 boules, et ces 2 événements sont équiprobables.
Pour information, l'expérience (non simplifiée) d'Ehrenfest (1880-1933) consiste à mettre $N$ boules numérotées dans l'urne A au départ.
L'idée est de modéliser la diffusion d'un gaz entre un compartiment A (contenant N molécules de gaz au départ) et un compartiment B (vide au départ).
On constate ici qu'avec N=2, l'état d'équilibre est réalisé une fois sur deux, mais que l'état initial peut revenir une fois sur 2.
En fait, si N est faible, le retour à l'état initial peut être fréquent.
Mais on peut montrer que le temps nécessaire au retour de toutes les boules dans l’urne A a pour espérance $2^N$, ce qui, pour un gaz (où N est très grand), peut être infiniment long...