Corrigé

PARTIE 1

1. La suite $(X_n)$ définit une chaîne de Markov car, à chaque étape $n$ , les probabilités de transition d'un état à un autre ne dépendent pas de $n$.
2. La distribution initiale du système est la suivante:
   $p(X_0=A)=0,7$      $p(X_0=B)=0,3$
3. Voici un arbre pondéré associé aux 2 premières transitions.
   
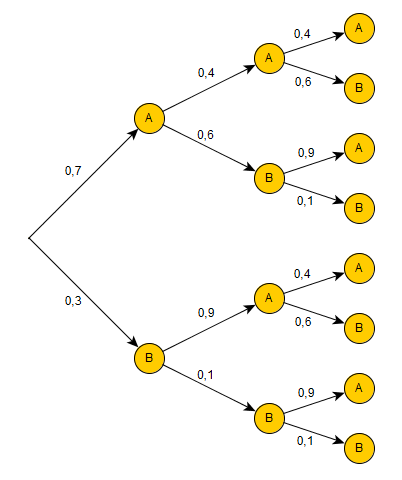
   Déterminons la distribution après ces 2 transitions.
   $\{A, B\}$ constitue une partition de l'univers. D'après la formule des probabilités totales, on obtient:
   $p(X_2=A)=0,7×0,4×0,4+0,7×0,6×0,9+0,3×0,9×0,4+0,3×0,1×0,9=0,625$
   $p(X_2=B)=1-p(X_2=A)=0,375$
   
4. Voici le graphe probabiliste et la matrice de transition demandés.
   
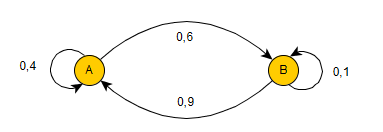
   $P=(\table 0.4,0.6;0.9,0.1)$
5. La distribution initiale du système est la suivante:
   $p(X_0=A)=0,7$      $p(X_0=B)=0,3$
   Donc: $π_0=(\table 0.7,0.3)$
   
   On sait que: $π_{2}=π_0×P^2$
   Or: $P=(\table 0.4,0.6;0.9,0.1)$
   Donc on obtient (à la calculatrice): $π_2=(\table 0.625,0.375)$
   On retrouve le fait que:
   $p(X_2=A)=0,625$       $p(X_2=B)=0,375$
6. On obtient (à la calculatrice): $π_{10}=π_0×P^{10}=(\table a,b)$
   où $a$ vaut environ 0,600 et $b$ vaut environ 0,400.
   La probabilité que le joueur A gagne la partie de rang 10 vaut environ 0,600, et la probabilité que le joueur B gagne la partie de rang 10 vaut environ 0,400.
7. On a: $P=(\table 0.4,0.6;0.9,0.1)$
   On constate tout d'abord que la matrice de transition $P$ ne comporte pas de zéro.
   Donc la suite $(π_n)$ converge vers une matrice de distribution $π$, unique solution de l'équation $π=π×P$.
   
   Résolvons l'équation $π=π×P$.
   On pose: $π=(\table a, b)$     avec $a+b=1$    (un détail à ne pas oublier!)
   Par conséquent: $π=(\table a, 1-a)$
   Donc: $π=π×P$ $ ⇔$ $\{\table a=a×0.4+(1-a)×0.9;1-a=a×0.6+(1-a)×0.1$
   Soit: $π=π×P$ $ ⇔$ $\{\table a=0.4a+0.9-0.9a;1-a=0.6a+0.1-0.1a$
   Soit: $π=π×P$ $ ⇔$ $\{\table 1.5a=0.9;-1.5a=-0.9$
   Soit: $π=π×P$ $ ⇔$ $a={0.9}/{1.5}=0.6$
   La solution unique de l'équation $π=π×P$ est $π=(\table 0.6,0.4)$, qui est la distribution invariante du système.
   
   La suite $(π_n)$ converge alors vers $π$, ce qui signifie que, lorsque le rang $n$ de la partie tend vers $+\∞$, la probabilité que le joueur A gagne tend vers $0,6$, la probabilité que le joueur B gagne tend vers $0,4$.
   A la longue, le joueur A gagne 6 parties sur 10.

PARTIE 2

1. Voici un arbre probabiliste correspondant à l'expérience.
   
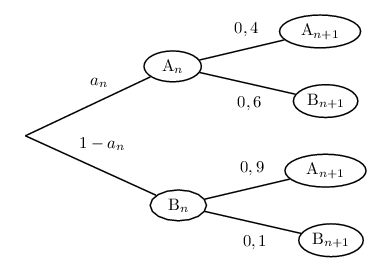
   $\{A_n;B_n\}$ constitue une partition de l'univers.
   On sait que $p(A_{n+1})=p(A_n∩A_{n+1})+p(B_n∩A_{n+1})$ (par application de la formule des probabilités totales).
   Soit: $p(A_{n+1})=p(A_n)×p_{A_n}(A_{n+1})+p(B_n)×p_{B_n}(A_{n+1})$
   Soit: $p(A_{n+1})=a_n×0,4+(1-a_n)×0,9$.
   Et par là: $a_{n+1}=0,9-0,5a_n$.
   C'est l'égalité cherchée.
2. On a: $v_n=a_n-0,6$
   Et par là: $v_{n+1}=a_{n+1}-0,6$
   Or: $a_{n+1}=0,9-0,5a_n$.
   Donc: $v_{n+1}==0,9-0,5a_n-0,6$
   Soit: $v_{n+1}==0,3-0,5a_n$
   Or, comme $v_n=a_n-0,6$, on a: $v_n+0,6=a_n$.
   Et par là, on obtient: $v_{n+1}==0,3-0,5(v_n+0,6)$
   Soit: $v_{n+1}==0,3-0,5v_n-0,3$
   Soit: $v_{n+1}==-0,5v_n$
   Et cette égalité est vraie pour tout naturel $n$.
   Par conséquent, la suite $(v_n)$ est géométrique de raison $-0,5$
3. Et par là: $v_n=v_0×(-0,5)^n$
   Or: $v_0=a_0-0,6=0,7-0,6=0,1$
   Donc: $v_n=0,1×(-0,5)^n$
   Et comme $v_n+0,6=a_n$, on obtient:
   $a_n=0,1×(-0,5)^n+0,6$
   Comme la raison $-0,5$ appartient à l'intervalle ]-1;1[, on en déduit que:
   $\lim↙{n→+∞} a_n=0,1×0+0,6=0,6$.
   On retrouve le fait que, lorsque le rang $n$ de la partie tend vers $+\∞$, la probabilité que le joueur A gagne tend vers $0,6$