 Combinatoire et dénombrement
Combinatoire et dénombrement
Dans tout ce qui suit, sauf indication contraire, $n$ et $k$ sont des entiers naturels.
I Ensembles et k-uplets
Principe additif
Soit deux ensembles A et B contenant respectivement $m$ et $n$ éléments et tels que leur intersection soit vide ($A⋂B=∅$), alors leur réunion $A∪B$ contient $m+n$ éléments.
Plus généralement, le nombre d'éléments d'une réunion d'ensembles 2 à 2 disjoints est égal à la somme des nombres d'éléments de chacun des ensembles.
Définition
Le produit cartésien de deux ensembles A et B, noté $A×B$, est l'ensemble des couples $(a,b)$,
où $a$ est un élément de $A$, et $b$ un élément de $B$.
$(a,b)$ s'appelle aussi bien un couple qu'un 2-uplet ou une 2-liste.
Le produit cartésien de $n$ ensembles $A_1$, $A_2$, ... ,$A_n$ noté $A_1×A_2× ... ×A_n$, est l'ensemble des n-uplets (ou n-listes) dont les composantes successives appartiennent respectivement à chacun des ensembles $A_1$, $A_2$, ... ,$A_n$.
Cas particulier: le produit cartésien de $k$ fois le même ensemble A se note $A^k$.
Un k-uplet (ou une k-liste) d'un ensemble A est un élément de $A^k$.
Principe multiplicatif
Soit deux ensembles A et B contenant respectivement $m$ et $n$ éléments, alors l’ensemble $A×B$ contient $m×n$ couples (ou "2-uplets", ou "2-listes").
Plus généralement, le nombre d'éléments d'un produit cartésien d'ensembles est égal au produit des nombres d'éléments de chacun des ensembles.
Cas particulier: le nombre de k-uplets (ou k-listes) d'un ensemble à n éléments est $n^k$.
Exemple
Soit $C=\{b,m\}$ et $V=\{a,e,i\}$
On pose $T=C∪V$.
Quel est le nombre d'éléments de $T$? Donner tous ces éléments.
Quel est le nombre d'éléments de $C×V$? Donner tous ces couples.
Quel est le nombre de de couples de $T$? Donner toutes ces couples.
Quel est le nombre de 3-uplets de $C$? Donner toutes ces 3-listes.
On a $T=C∪V$. Or, C contient 2 éléments, et V contient 3 éléments. Et comme C et V sont disjoints (ils n'ont pas d'élément en commun), le nombre d'éléments de $T$ est donc égal à 5
(on a fait la somme $2+3=5$).
Notons que $T=\{b,m,a,e,i\}$
C contient 2 éléments. V contient 3 éléments. Donc le nombre de couples de $C×V$ est égal à 6
(on a fait le produit $2×3=6$).
Notons que $C×V=\{(b,a),(b,e),(b,i),(m,a),(m,e),(m,i)\}$
On a vu que $T$ contient 5 éléments, donc le nombre de 2-listes de $T$ est égal à 25 (on a fait le calcul $5^2=25$).
Les 25 listes sont: (b,b),(b,m),(b,a),(b,e),(b,i),(m,b),(m,m),(m,a),(m,e),(m,i),(a,b),(a,m),(a,a),(a,e),(a,i),(e,b),(e,m),(e,a),(e,e),(e,i),(i,b),(i,m),(i,a),(i,e),(i,i).
Il est facile de les obtenir avec un arbre de dénombrement ayant $5×5=25$ feuilles.
Concrètement, cela correspond aux 25 mots de 2 lettres que l'on peut obtenir à partir d'un alphabet contenant 5 lettres.
$C$ contient 2 éléments, donc le nombre de 3-listes de $C$ est égal à 8 (on a fait le calcul $2^3=8$).
Les 8 listes sont: (b,b,b) (b,b,m) (b,m,b) (b,m,m) (m,b,b) (m,b,m) (m,m,b) (m,m,m).
Il est facile de les obtenir avec un arbre de dénombrement ayant $2×2×2=8$ feuilles.
Concrètement, cela correspond aux 8 mots de 3 lettres que l'on peut obtenir à partir d'un alphabet contenant 2 lettres.
A retenir
Dans un k-uplet, l'ordre est essentiel, et la répétition est possible.
II Arrangements sans répétition
Définition
Soit $n$ un entier naturel. Le produit des entiers naturels non nuls et inférieurs à $n$ s'appelle factorielle de n.
On dit aussi factorielle n, ou n factorielle
Ce produit se note $n!$
On obtient alors: $0!=1$ (par convention, un produit vide vaut 1)
$1!=1$, $2!=2×1=2$, $3!=3×2×1=6$, $4!=4×3×2×1=24$
Et pour les entiers naturels $n$ qui suivent: $n!=n×(n-1)×(n-2)×...×2×1$
Exemple
Déterminer une valeur de $a=30!$ arrondie à $10^{30}$.
Déterminer la valeur exacte de $b={100!}/{97!}$
On a: $a=30!=30×29×28×...×2×1≈2,6525.10^{32}$ (à l'aide de l'instruction factorielle de la calculatrice)
Donc: $a≈2,65.10^{32}$ arrondie à $0,01.10^{32}=10^{30}$.
La calculatrice ne permet de calculer ni $100!$, ni $97!$ (dépassement de capacité)
Mais on a: $b={100!}/{97!}={100×99×98×97×...×2×1}/{97×96×...×2×1}=100×99×98=970\,200$
Définition
Un k-uplets d'éléments distincts d'un ensemble à n éléments s'appelle un arrangement sans répétition de k éléments pris parmi n.
Le nombre d'arrangements sans répétition de k éléments pris parmi n se note $\A_n^k$.
A retenir
Dans un arrangement sans répétition, l'ordre est essentiel, et la répétition est impossible.
Propriété
On a l'égalité: $\A_n^k={n!}/{(n-k)!}$ (pour $≤k≤n$)
On notera que $\A_n^k=n×(n-1)×(n-2)×...×(n-k+1)$ (pour $≤k≤n$)
Si $k>n$, alors $\A_n^k=0$ (il est alors impossible de prendre $k$ éléments distincts parmi $n$)
Propriété et définition
Une permutation sur un ensemble à $n$ éléments est un arrangement sans répétition de n éléments de l'ensemble (pris parmi n).
Le nombre de permutations d'un ensemble à $n$ éléments est donc égal à $\A_n^n=n!$
Exemple
Soit $E=\{a,b,c,d\}$.
Quel est le nombre de mots de 2 lettres distinctes que l'on peut composer à partir des lettres de E? Donner les.
Quel est le nombre de mots de 4 lettres distinctes que l'on peut composer à partir des lettres de E? Donner les.
Corrigé
Les mots avec des lettres distinctes correspondent à des arrangements.
Comme $E$ a 4 éléments, le nombre de mots de 2 lettres distinctes est 12
(on a fait le calcul: $\A_4^2={4!}/{(4-2)!}={4×3×2×1}/{2×1}=4×3=12$).
Ces mots s'obtiennent à l'aide d'un arbre de dénombrement.
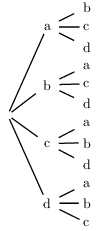
Ces mots sont: ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc
Les mots avec 4 lettres distinctes parmi 4 correspondent à des permutations.
Comme $E$ a 4 éléments, le nombre de mots de 4 lettres distinctes est 24
(on a fait le calcul: $\A_4^4=4!=4×3×2×1=24$).
Ces mots s'obtiennent à l'aide d'un arbre de dénombrement du type précédent.
Ces mots sont:
abcd, abdc, acbd, acdb, adbc, adcb,
bacd, badc, bcad, bcda, bdac, bdca,
cabd, cadb, cbad, cbda, cdab, cdba,
dabc, dacb, dbac, dbca, dcab, dcba
III Combinaisons
Propriété
Le nombre de parties d'un ensemble à $n$ éléments est égal à $2^n$.
Exemple
Soit $V=\{a,b,c\}$. Quel est le nombre de parties de $V$? Les donner toutes.
Quel est le nombre de 3-uplets de $\{0,1\}$? Donner tous ces 3-uplets.
Proposer une méthode permettant d'associer à chaque 3-uplet de $\{0,1\}$ une partie de $V$, les parties étant toutes différentes.
Que peut-on vérifier alors?
Corrigé
Comme $V$ a 3 éléments, le nombre de parties de $V$ est 8 (on a fait le calcul: $2^3=8$).
Ces parties sont: $\{\,\}$, $\{a\}$, $\{b\}$, $\{c\}$, $\{a , b\}$, $\{a , c\}$, $\{b , c\}$, $\{a, b, c\}$.
La partie vide se note $\{\,\}$ ou $\∅$.
$V=\{a, b, c\}$ est une partie de lui-même.
Dans une partie, l'ordre n'intervient pas.
Comme $\{0,1\}$ a 2 éléments, le nombre de 3-uplets de $\{0,1\}$ est 8
(on a fait le calcul: $2^3=8$).
Ces 3-uplets sont: (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0) et (1,1,1).
Ils s'obtiennent facilement à l'aide d'un arbre de dénombrement.
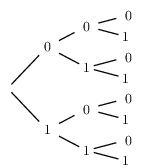
Voici une méthode permettant d'associer à chaque 3-uplet de $\{0,1\}$ une partie de $V$, les parties étant toutes différentes.
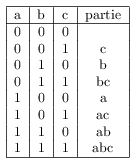
A chaque ligne du tableau correspond une partie qui contient uniquement les lettres affectées d'un 1.
La première ligne correspond à l'ensemble vide, qui est une partie de V.
La seconde ligne correspond au singleton $\{c\}$...etc...
La dernière ligne correspond à l'ensemble $V$, qui est la plus grande partie de lui-même.
On constate donc que le nombre de parties de $V$ (qui contient 3 éléments) est égal au nombre de 3-uplets de $\{0,1\}$, c'est à dire $2^n$.
Définition
Une partie à $k$ éléments d'un ensemble à $n$ éléments s'appelle combinaison de k éléments parmi n.
Le nombre de combinaisons de k éléments pris parmi n se note $(\table n; k)$.
Si nous tirons sans remise $k$ objets parmi $n$ objets discernables, et nous les disposons sans tenir compte de l'ordre d'apparition, nous pouvons représenter ces $k$ objets par une partie à $k$ éléments d'un ensemble à $n$ éléments.
Ce sont des combinaisons sans répétition de $k$ éléments parmi $n$.
A retenir
Dans une partie (ou une combinaison), l'ordre n'intervient pas, et la répétition est impossible.
On obtient directement les coefficients $(\table n; k)$ avec les calculatrices:
Casio: OPTN PROB n nCr k
TI: MATH PRB n Combinaison k
Propriété
On a l'égalité: $(\table n; k)={n!}/{(n-k)!k!}$ (pour $0≤k≤n$)
On notera que $(\table n; k)={\A_n^k}/{k!}={n×(n-1)×(n-2)×...×(n-k+1)}/{k!}$ (pour $0≤k≤n$)
Si $k>n$, alors $(\table n; k)=0$ (il est alors impossible de prendre $k$ éléments distincts parmi $n$)
Exemple
Soit $E=\{7, 8, 9, 10, V, D, R, As\}$.
Quel est le nombre de mains de 3 cartes que l'on peut composer à partir des 8 cartes de E?
Soit $F=\{ V, D, R\}$.
Quel est le nombre de mains de 2 cartes que l'on peut composer à partir des 3 cartes de F? Donner les.
Corrigé
Les mains correspondent à des combinaisons.
Comme $E$ a 8 éléments, le nombre de mains de 3 cartes est 56
(on a fait le calcul: $(\table 8; 3)={8×7×6}/{3!}={8×7×6}/{3×2×1}=8×7=56$).
Comme $F$ a 3 éléments, le nombre de mains de 2 cartes est 3
(on a fait le calcul: $(\table 3; 2)={3×2}/{2!}={3×2}/{2×1}=3$).
Il s'agit de $\{V,D\}$, $\{V,R\}$ et $\{D,R\}$.
On rappelle que l'ordre des éléments n'a pas d'importance dans une combinaison.
Exemple
On répète 4 fois une expérience ayant 2 issues S et E. On dresse l'arbre dénombrant toutes les possibilités.
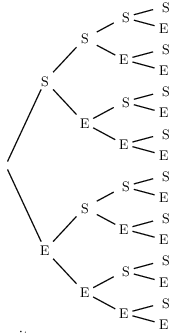
Dénombrer le nombre de chemins permettant d'obtenir exactement 2 issues S.
Corrigé
Une issue S peut survenir en première, seconde, troisième ou quatrième position.
On associe à chaque issue S son rang d'apparition (entre 1 et 4).
Chaque chemin favorable correspond donc à une combinaison de 2 rangs parmi 4. Par exemple, la combinaison $\{1,3\}$ correspond au chemin (S,E,S,E).
Le nombre de chemins permettant d'obtenir exactement 2 issues S est donc égal à 6
(on a fait le calcul: $(\table 4; 2)={4×3}/{2!}={4×3}/{2×1}=6$).
Propriété
$(\table n; 0)=1$ $(\table n; 1)=n$ (pour $n≥1$) $(\table n; 2)={n×(n-1)}/{2}$ (pour $n≥2$)
Propriété de symétrie
Pour tous les entiers $n$ et $k$ tels que $0≤k≤n$
$(\table n; k)=(\table n; n-k)$
Relation de Pascal
Pour tous les entiers $n$ et $k$ tels que $0$<$k$<$n$
$(\table n; k)=(\table n-1; k-1)+(\table n-1; k)$
Exemple
Cet exercice se fait sans calculatrice, et en utilisant les propriétés précédentes.
On suppose que $(\table 13; 3)=286$, $(\table 13; 4)=715$ et $(\table 14; 6)=3003$.
- Déterminer $(\table 12; 2)$, $(\table 13; 10)$, $(\table 14; 4)$ et $(\table 12; 3)$
- On pose $s=(\table 5; 5)+(\table 6; 5)+(\table 7; 5)+...(\table 12; 5)+(\table 13; 5)$
Démontrer que $s=3003$
Corrigé
- On a: $(\table 12; 2)={12×11}/{2}=6×11=$$66$
Par symétrie, on a: $(\table 13; 10)=(\table 13;13- 10)$
Soit: $(\table 13; 10)=(\table 13;3)=$$286$
D'après la relation de Pascal, on a: $(\table 14; 4)=(\table 13; 3)+(\table 13; 4)=286+715=$$1001$
D'après la relation de Pascal, on a: $(\table 13; 3)=(\table 12; 2)+(\table 12; 3)$
Et donc: $(\table 12; 3)=(\table 13; 3)-(\table 12; 2)=286-66=$$220$ - D'après la relation de Pascal, on a:
$(\table 6; 6)+(\table 6; 5)=(\table 7; 6)$
Et donc: $(\table 6; 5)=(\table 7; 6)-(\table 6; 6)$
De même, on obtient: $(\table 7; 5)=(\table 8; 6)-(\table 7; 6)$ et $(\table 8; 5)=(\table 9; 6)-(\table 8; 6)$ ...etc... $(\table 13; 5)=(\table 14; 6)-(\table 13; 6)$
Donc: $s=(\table 5; 5)+(\table 7; 6)-(\table 6; 6)+(\table 8; 6)-(\table 7; 6)...+(\table 14; 6)-(\table 13; 6)$
On constate que, par un jeu de dominos, presque tous les termes s'annulent. Il reste:
$s=(\table 5; 5)-(\table 6; 6)+(\table 14; 6)$
Or, on a: $(\table 5; 5)=(\table 6; 6)=1$
Et par ailleurs, on sait que: $(\table 14; 6)=3003$
Donc: $s=3003$