 Continuité
Continuité
I Fonctions continues
Définition
Soit $f$ une fonction définie sur un intervalle I. Soit $a$ dans I.
$f$ est continue en $a$ si et seulement si $\lim↙{x→a}f(x)=f(a)$.
$f$ est continue sur I si et seulement si $f$ est continue en tout nombre $a$ de I.
Graphiquement, une fonction est continue quand le tracé de sa courbe représentative peut se faire sans lever le crayon.
Exemple
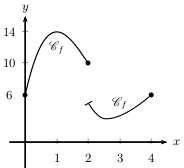
La fonction $f$ est continue sur l'intervalle $\[0;2\]$.
La fonction $f$ est continue sur l'intervalle $\]2;4\]$.
Mais la fonction $f$ n'est pas continue sur l'intervalle $\[0;4\]$ car elle est discontinue en 2!
Propriété
Soit $f$ une fonction définie sur un intervalle I. Soit $a$ dans I.
Si $f$ est dérivable en $a$, alors $f$ est continue en $a$.
Si $f$ est dérivable sur I, alors $f$ est continue sur I.
Définition et propriété
Les fonctions polynômes, la fonction valeur absolue, la fonction racine carrée, la fonction exponentielle,
la fonction logarithme népérien, les fonctions cosinus et sinus constituent les fonctions usuelles.
Les fonctions usuelles, ainsi que les fonctions obtenues par opérations ou par composition usant de fonctions usuelles,
sont continues sur les intervalles sur lesquels elles sont définies.
Exemple
La fonction $f(x)=(3x^2-5)e^{x-7}$ est-elle continue sur $\R$?
$f$ est définie sur $\R$.
Et $f$ est obtenue par opérations ou par composition de fonctions usuelles.
Donc $f$ est continue sur $\R$.
II Suites composées
Propriété
Si $f$ est une fonction continue en $l$, et si $\lim↙{n→+∞}u_n=l$, alors la suite composée $f(un)$ converge vers $f(l)$.
Exemple
Soit $f$ définie pour tout $x$ de $\R$ par $f(x)=x^2+3$.
On considère la suite $(u_n)$, définie pour tout naturel $n$ par $u_n={1}/{n}+2$,
et la suite $(v_n)$ définie pour tout naturel $n$ par $v_n=f(u_n)$.
Déterminer $\lim↙{n→+∞}v_n$.
On a: $\lim↙{n→+∞}u_n=0+2=2$
Or la fonction $f(x)=x^2+3$, obtenue par opérations de fonctions usuelles continues, est continue sur $\R$, en particulier en 2.
Donc la suite $(v_n)=(f(u_n))$ converge,
et on a: $\lim↙{n→+∞}v_n=f(2)$
Soit: $\lim↙{n→+∞}v_n=7$
 Exemple
Exemple
Soit $(u_n)$ une suite définie par:
$u_0=50$,
et par la relation de récurrence $u_{n+1}=0,5u_n+10$ (pour tout naturel $n$).
On suppose que $(u_n)$ est convergente, et que $\lim↙{n→+∞}u_n=l$.
Montrer que $l=20$.
Corrigé
On a: $\lim↙{n→+∞}u_n=l$
Donc, comme la fonction affine $0,5x+10$ est continue sur $\R$, on obtient: $\lim↙{n→+∞}0,5u_n+10=0,5l+10$.
Par ailleurs, comme $\lim↙{n→+∞}u_n=l$, on a aussi: $\lim↙{n→+∞}u_{n+1}=l$
On a donc $\lim↙{n→+∞}0,5u_n+10=0,5l+10$ et $\lim↙{n→+∞}u_{n+1}=l$
Par conséquent, comme $u_{n+1}=0,5u_n+10$, on obtient finalement (par unicité de la limite):
$l=0,5l+10$
Et par là: $l=20$
Une rédaction plus concise est la suivante.
On suppose que $\lim↙{n→+∞}u_n=l$.
Or ici, $u_{n+1}=f(u_n)$ avec $f(x)=0,5x+10$.
Donc, comme $f$ est continue, par passage à la limite, on obtient:
$l=0,5l+10$
Et par là: $l=20$
Savoir faire
La propriété précédente permet donc de trouver la limite d'une suite définie par récurrence, dès lors qu'on est assuré de son existence.
Ainsi, si $\lim↙{n→+∞}u_n=l$, si $u_{n+1}=f(u_n)$, et si $f$ est continue, alors $l$ est solution de l'équation $l=f(l)$.
III Equations $f(x)=k$
Théorème des valeurs intermédiaires
Si $f$ est une fonction continue sur $\[a;b\]$,
Si $k$ est un nombre compris entre $f(a)$ et $f(b)$,
Alors l'équation $f(x)=k$ admet au moins une solution sur $\[a;b\]$.
Propriété
Par convention, dans un tableau de variation, les flèches indiquent évidemment que la fonction est strictement monotone, mais aussi qu'elle est continue.
Exemple
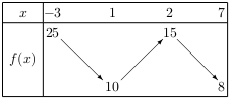
La fonction $f$ vérifie le tableau de variation ci-dessous.
Montrer que l'équation $f(x)=12$ admet au moins une solution sur $\[-3;7\]$.
Corrigé
D'après le tableau de variation ci-dessus, la fonction $f$ est continue sur $\[-3;7\]$.
Or, 12 est un nombre compris entre $f(-3)=25$ et $f(7)=8$,
Donc, d'après le théorème des valeurs intermédiaires, l'équation $f(x)=12$ admet au moins une solution sur $\[-3;7\]$.
Théorème de la bijection
Si $f$ est une fonction continue et strictement monotone sur $\[a;b\]$,
Si $k$ est un nombre compris entre $f(a)$ et $f(b)$,
Alors l'équation $f(x)=k$ admet une unique solution sur $\[a;b\]$.
 Exemple
Exemple
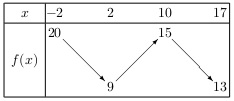
La fonction $f$ vérifie le tableau de variation ci-dessous.
Montrer que l'équation $f(x)=12$ admet exactement 2 solutions, la première entre -2 et 2, la seconde entre 2 et 10.
Corrigé
D'après le tableau de variation ci-dessus, la fonction $f$ est continue et strictement décroissante sur $\[-2;2\]$.
Or 12 est un nombre compris entre $f(-2)=20$ et $f(2)=9$,
Donc, d'après le théorème de la bijection, l'équation $f(x)=12$ admet une unique solution $c_1$ sur $\[-2;2\]$.
De même, nous pouvons démontrer que l'équation $f(x)=12$ admet admet une unique solution $c_2$ sur $\[2;10\]$.
Enfin, comme 13 est le minimum de $f$ sur $\[10;17\]$, l'équation $f(x)=12$ n'admet pas de solution sur $\[10;17\]$.
Il est clair que: $-2$<$ c_1$<$2$<$ c_2$<$10$. L'équation $f(x)=12$ admet donc exactement 2 solutions, la première entre -2 et 2, la seconde entre 2 et 10.
Généralisation
Les théorèmes des valeurs intermédiaires et de la bijection s'étendent naturellement
à des intervalles semi-ouverts ou ouverts, bornés ou non.
Voir l'exemple ci-dessous.
 Exemple
Exemple
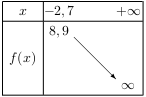
La fonction $f$ vérifie le tableau de variation ci-dessous.
Montrer que l'équation $f(x)=1$ admet exactement 1 solution sur $[-2,7;+∞[$.
Corrigé
D'après le tableau de variation ci-dessus, la fonction $f$ est continue et strictement décroissante sur $[-2,7;+∞[$.
Or 1 est strictement inférieur à $f(-2,7)=8,9$, et $\lim↙{x→+∞}f(x)=-∞$.,
Donc, d'après le théorème de la bijection, l'équation $f(x)=1$ admet une unique solution sur $[-2,7;+∞[$.
A quoi peut servir le théorème de la bijection ?
On est parfois confronté à des équations difficiles à résoudre algébriquement. Il est alors tentant de lancer un programme qui permettra d'encadrer la solution recherchée. Mais encore faut-il qu'elle existe, et qu'elle soit unique sur l'intervalle d'étude !
Par application du théorème de la bijection, on est assuré que le programme nous donnera un résultat satisfaisant.