 Vecteurs, droites et plans de l'espace
Vecteurs, droites et plans de l'espace
I Droites et plans de l'espace
Remarque: quelques mises au point pour commencer avant de manipuler les vecteurs de l'espace...
Propriété
Deux droites de l'espace sont:
soit coplanaires (dans un même plan), soit non coplanaires.
Deux droites coplanaires sont;
soit parallèles , soit sécantes .
Deux droites parallèles sont:
soit strictement parallèles, soit confondues .
Exemple
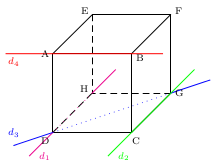
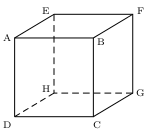
ABCDEFGH est un cube.
$d_1=(DH)$ $d_2=(CG)$
$d_3=(DG)$ $d_4=(AB)$
Les droites $d_4$ et $d_3$ ne sont pas coplanaires.
Les droites $d_3$ et $d_2$ sont coplanaires et sécantes en G.
Les droites $d_1$ et $d_2$ sont coplanaires et strictement parallèles.
Les droites $d_1$ et $(DH)$ sont coplanaires et confondues.
Propriété
Une droite et un plan de l'espace sont:
soit sécants selon un point, soit parallèles .
Une droite et un plan parallèles sont:
soit strictement parallèles, soit tels que la droite est dans le plan.
Exemple
Dans la figure du premier exemple:
Le plan $(AEH)$ et la droite $d_3$ sont sécants au point D.
Le plan $(AEH)$ et la droite $d_2$ sont strictement parallèles.
Le plan $(AEH)$ et la droite $d_1$ sont parallèles et $d_1$ est dans le plan $(AEH)$.
Propriété
Deux plans de l'espace sont:
soit sécants selon une droite, soit parallèles .
Deux plans parallèles sont:
soit strictement parallèles, soit confondus .
Exemple
Reprenons la figure du premier exemple:
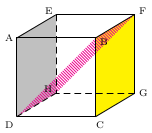
Les plans $(AEH)$ et $(BFD)$ sont sécants selon la droite $(DH)$.
Les plans $(AEH)$ et $(BCG)$ sont strictement parallèles.
Les plans $(AEH)$ et $(DAH)$ sont parallèles et confondus.
 Exemple
Exemple
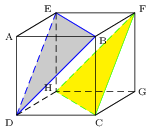
ABCD est un tétraèdre non aplati représenté ci-dessous en perspective cavalière.
X est le milieu de l'arête [AB], Y est sur l'arête [BC], mais n'est pas le milieu de [BC], Z est le mileu de l'arête [AD].
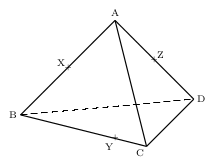
Il est clair que les points X et Z sont dans le plan (ABD).
Nous allons déterminer la section du tétraèdre ABCD par le plan (XYZ).
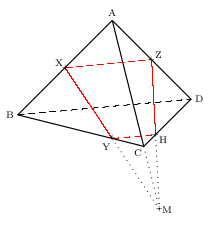
- Les droites (XY) et (AC) sont-elles coplanaires?
-
a.
 Les droites (XY) et (AC) sont sécantes. Pourquoi?
Les droites (XY) et (AC) sont sécantes. Pourquoi?
b. Pourquoi leur point d'intersection M appartient-il à la fois au plan (XYZ) et au plan (ACD)?
c. Quel autre point appartient à la fois au plan (XYZ) et au plan (ACD)? -
a.
 Montrer que le point X ne peut appartenir au plan (ACD) (raisonner par l'absurde).
Montrer que le point X ne peut appartenir au plan (ACD) (raisonner par l'absurde).
b. Pourquoi les plans (XYZ) et (ACD) sont-ils sécants?
c. Tracer la droite intersection de (XYZ) et (ACD). -
Construire la section du tétraèdre par le plan (XYZ)
(On ne demande pas de justification, mais il faudra laisser les traits de construction.
La section sera repassée en rouge)
Corrigé
- X est sur [AB], donc X est dans le plan (ABC).
Y est sur [BC], donc Y est dans le plan (ABC).
Et comme X et Y sont dans le plan (ABC), la droite (XY) est dans le plan (ABC).
Par ailleurs, il est évident que la droite (AC) est dans le plan (ABC).
Finalement, (XY) et (AC) sont coplanaires (dans le plan (ABC)). - a. Considérons le triangle ABC, dont X est le milieu du côté [AB].
Si (XY) et (AC) étaient parallèles, alors Y serait le milieu de [BC], ce qui contraire à l'hypothèse.
Donc les droites coplanaires (XY) et (AC) ne peuvent qu'être sécantes.
b. Le point M est sur la droite (XY), donc il est dans le plan (XYZ).
Le point M est sur la droite (AC), donc il est dans le plan (ACD).
Finalement, M appartient à la fois au plan (XYZ) et au plan (ACD).
c. Le point Z est évidemment dans (XYZ).
Et comme il est sur [AD], il est dans (ACD).
Z appartient donc à la fois au plan (XYZ) et au plan (ACD). -
a. Si X appartenait au plan (ACD), alors, comme A est dans (ACD),
la droite (AX) y serait aussi, et par là, le point B serait dans le plan (ADC).
Le tétraèdre ABCD serait aplati, ce qui est contraire à l'hypothèse.
Donc, finalement, X ne peut appartenir au plan (ACD).
b. Z est dans (XYZ). Or, Z étant sur [AC], Z est dans (ACD).
Donc les plans (XYZ) et (ACD) ont au moins un point commun.
Par conséquent, ils sont soit confondus, soit sécants.
Or, ils ne peuvent être confondus car X appartient à (XYZ) mais n'appartient pas à (ACD).
Donc ils sont sécants.
c. M et Z sont à la fois dans les plans (XYZ) et (ACD), donc ces plans se coupent selon la droite (ZM).
-
La section est XYHZ.
II Vecteurs de l'espace
Remarque: les définitions et propriétés relatives aux vecteurs du plan s'étendent à l'espace. En voici quelques unes.
Propriétés
ABDC est un parallélogramme
si et seulement si ${AB}↖{→}={CD}↖{→}$.
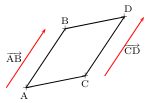
ABDC est un parallélogramme si et seulement si
D est l'image de C par la translation de vecteur ${AB}↖{→}$.
Règle du parallélogramme:
ABDC est un parallélogramme si et seulement si ${AB}↖{→}+{AC}↖{→}={AD}↖{→}$.
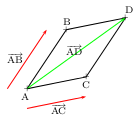
Propriétés
Relation de Chasles:
${AB}↖{→}+{BC}↖{→}={AC}↖{→}$.
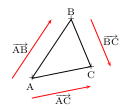
Milieu et vecteurs opposés:
Le point I est le milieu de [AB] si et seulement si ${AI}↖{→}=-{BI}↖{→}$.
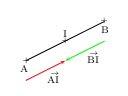
Exemple
ABCDS est une pyramide de sommet S dont la base ABCD est un parallélogramme.
Démontrer que ${SD}↖{→}+ {SB}↖{→}= {SC}↖{→}+ {SA}↖{→}$.
Corrigé
ABCD est un parallélogramme, donc: ${AB}↖{→}= {DC}↖{→}$, et donc: ${AB}↖{→}+{CD}↖{→}={0}↖{→}$ (1).
${SD}↖{→}+ {SB}↖{→}={SC}↖{→}+ {CD}↖{→}+{SA}↖{→}+ {AB}↖{→}$ (Chasles)
D'où: ${SD}↖{→}+ {SB}↖{→}= {SC}↖{→}+ {SA}↖{→}+{0}↖{→}$ (d'après (1))
Soit: ${SD}↖{→}+ {SB}↖{→}= {SC}↖{→}+ {SA}↖{→}$.
III Combinaisons linéaires et bases
a. Combinaisons linéaires
Définition
Si ${u_1}↖{→}$, ${u_2}↖{→}$, ..., ${u_n}↖{→}$ sont $n$ vecteurs, et si $a_1$, $a_2$,..., $a_n$ sont $n$ réels,
alors le vecteur $a_1 .{u_1}↖{→}+a_2 .{u_2}↖{→}+ ...+a_n .{u_n}↖{→}$ est une combinaison linéaire des vecteurs ${u_1}↖{→}$, ${u_2}↖{→}$, ...et ${u_n}↖{→}$.
Exemple
Reprenons la figure du premier exemple:
Exprimer le vecteur ${DG}↖{→}$ comme combinaison linéaire des vecteurs ${DC}↖{→}$ et ${DH}↖{→}$.
Exprimer le vecteur ${DF}↖{→}$ comme combinaison linéaire des vecteurs ${DC}↖{→}$, ${DH}↖{→}$ et ${DA}↖{→}$.
Corrigé
Comme la figure est un cube, ses faces sont des carrés, et donc des parallélogrammes.
Et donc, comme DCGH est un parallélogramme, on a: ${DG}↖{→}= {DC}↖{→}+{DH}↖{→}$.
L'écriture ${DG}↖{→}=1.{DC}↖{→}+1.{DH}↖{→}$ montre clairement que ${DG}↖{→}$ est une combinaison linéaire des vecteurs ${DC}↖{→}$ et ${DH}↖{→}$.
D'après la relation de Chasles, on a: ${DF}↖{→}={DG}↖{→}+{GF}↖{→}$
Or, on a vu que: ${DG}↖{→}= {DC}↖{→}+{DH}↖{→}$
Et comme la figure est un cube, on a de plus: ${GF}↖{→}={DA}↖{→}$
Donc on obtient finalement: ${DF}↖{→}={DC}↖{→}+{DH}↖{→}+{DA}↖{→}$
Ce qui montre que ${DF}↖{→}$ est une combinaison linéaire des vecteurs ${DC}↖{→}$, ${DH}↖{→}$ et ${DA}↖{→}$.
b. Les droites de l'espace
Définition
Le vecteur nul ${0}↖{→}$ est colinéaire à tout vecteur.
Deux vecteurs non nuls ${u}↖{→}$ et ${v}↖{→}$ sont colinéaires si et seulement si
il existe un réel $k$ tel que ${v}↖{→}=k.{u}↖{→}$
Propriétés et définitions
Soient A et B deux points distincts.
M appartient à la droite (AB) si et seulement si il existe un nombre réel $k$ tel que ${AM}↖{→}=k{AB}↖{→}$.
${AB}↖{→}$ est un vecteur directeur de la droite (AB).
Remarque:
Une droite peut être définie:
par 2 points distincts,
ou: par un point et un vecteur directeur (nécessairement non nul).
Définitions et propriétés
On considère une droite de vecteur directeur ${u}↖{→}$.
La direction (vectorielle) $\D$ de cette droite est l'ensemble de tous les vecteurs colinéaires à ${u}↖{→}$.
${v}↖{→}$ appartient à $\D$ si et seulement si il existe un réel $k$ tel que ${v}↖{→}=k.{u}↖{→}$
Le vecteur ${u}↖{→}$ constitue alors une base de la direction vectorielle D.
Le réel $k$ est unique et s'appelle la coordonnée de ${v}↖{→}$ dans la base ${u}↖{→}$.
Propriété
On considère deux droites de vecteurs directeurs respectifs ${u}↖{→}$ et ${v}↖{→}$
Ces droites sont parallèles
si et seulement si elles ont la même direction (vectorielle)
si et seulement si ${u}↖{→}$ et ${v}↖{→}$ sont colinéaires.
c. Les plans de l'espace
Propriétés et définitions
Soient A, B et C trois points non alignés.
M appartient au plan (ABC) si et seulement si il existe deux nombres réels $x$ et $y$ tels que
${AM}↖{→}=x{AB}↖{→}+y{AC}↖{→}$.
Le couple (${AB}↖{→}$ , ${AC}↖{→}$) est un couple de vecteurs directeurs du plan (ABC).
Remarque:
Un plan peut être défini:
par 3 points non alignés,
ou: par un point et deux vecteurs directeurs (nécessairement non colinéaires).
Définitions et propriétés
On considère un plan de vecteurs directeurs ${u}↖{→}$ et ${v}↖{→}$.
La direction (vectorielle) $\P$ de ce plan est l'ensemble de tous les vecteurs combinaisons linéaires de ${u}↖{→}$ et de ${v}↖{→}$.
${w}↖{→}$ appartient à $\P$ si et seulement si il existe deux réels $a$ et $b$ tel que ${w}↖{→}=a.{u}↖{→}+b.{v}↖{→}$
Le couple de vecteurs $({u}↖{→},{v}↖{→})$ constitue alors une base du plan vectoriel $\P$.
Le couple de réels $(a,b)$ est unique et s'appelle les coordonnées de ${w}↖{→}$ dans la base $({u}↖{→},{v}↖{→})$.
Remarque.
Par abus de langage, il est fréquent de confondre un plan et sa direction vectorielle.
Propriétés
On considère deux plans de couples de vecteurs directeurs respectifs (${u}↖{→}$,${v}↖{→}$) et (${u'}↖{→}$,${v'}↖{→}$)
Ces plans sont parallèles
si et seulement si ils ont la même direction (vectorielle)
si et seulement si ${u'}↖{→}$ et ${v'}↖{→}$ sont chacun combinaison linéaire de ${u}↖{→}$ et ${v}↖{→}$.
On considère une droite de vecteur directeur ${u}↖{→}$ et un plan de direction vectorielle $\P$
La droite est parallèle au plan
si et seulement si la direction (vectorielle) de la droite est incluse dans celle du plan
si et seulement si ${u}↖{→}$ appartient à la direction vectorielle $\P$
Exemple
Reprenons encore une fois la figure du premier exemple:
Démontrer que les plans (DBE) et (CFH) sont parallèles.
Corrigé
Les vecteurs ${EB}↖{→}$ et ${ED}↖{→}$ sont vecteurs directeurs du plan (DBE).
Les vecteurs ${HC}↖{→}$ et ${FC}↖{→}$ sont vecteurs directeurs du plan (CFH).
Or, comme ABCDEFGH est un cube, les vecteurs ${CB}↖{→}$ et ${HE}↖{→}$ sont égaux, et par là, HEBC est un parallélogramme, et donc, les vecteurs ${EB}↖{→}$ et ${HC}↖{→}$ sont égaux.
De même, on peut montrer que les vecteurs ${ED}↖{→}$ et ${FC}↖{→}$ sont égaux.
Donc finalement, les plans (DBE) et (CFH) ont les mêmes vecteurs directeurs.
Donc les plans (DBE) et (CFH) sont parallèles.
Notons que l'égalité des bases n'est pas indispensable; il aurait suffit que ${HC}↖{→}$ et ${FC}↖{→}$ soient combinaisons linéaires de ${EB}↖{→}$ et ${ED}↖{→}$ pour démontrer le parallélisme.
Définition
Les points A, B, C et D sont coplanaires
si et seulement si ils appartiennent à un même plan.
Les vecteurs ${u}↖{→}$, ${v}↖{→}$ et ${w}↖{→}$ sont coplanaires
si et seulement si ils appartiennent à une même direction vectorielle de plan.
Les vecteurs ${u}↖{→}$, ${v}↖{→}$ et ${w}↖{→}$ sont linéairement indépendants
si et seulement si ils ne sont pas coplanaires.
Propriété
Si ${u}↖{→}$ et ${v}↖{→}$ sont deux vecteurs non colinéaires, alors:
les vecteurs ${u}↖{→}$, ${v}↖{→}$ et ${w}↖{→}$ sont coplanaires
si et seulement si il existe des nombres réels $x$ et $y$ tels que ${w}↖{→}=x{u}↖{→}+y{v}↖{→}$.
d. Les bases de l'espace
Propriété
Les trois vecteurs ${u}↖{→}$, ${v}↖{→}$ et ${w}↖{→}$ sont linéairement indépendants (c'est à dire non coplanaires)
si et seulement si $a{u}↖{→}+b{v}↖{→}+c{w}↖{→}={0}↖{→}$ implique que $a=b=c=0$.
Définition
Trois vecteurs non coplanaires ${i}↖{→}$, ${j}↖{→}$ et ${k}↖{→}$ définissent une base de l'espace (vectoriel),
notée $({i}↖{→},{j}↖{→},{k}↖{→})$.
Un point O et trois vecteurs non coplanaires ${i}↖{→}$, ${j}↖{→}$ et ${k}↖{→}$ définissent un repère de l'espace,
noté $(O,{i}↖{→},{j}↖{→},{k}↖{→})$.
Définition et propriété
Soient $({i}↖{→},{j}↖{→},{k}↖{→})$ une base de l'espace.
Pour tout vecteur ${v}↖{→}$, il existe un triplet $(x;y;z)$ de nombres réels tel que ${v}↖{→}=x{i}↖{→}+y{j}↖{→}+z{k}↖{→}$.
Le triplet de réels $(x,y,z)$ est unique et s'appelle les coordonnées de ${v}↖{→}$ dans la base $({i}↖{→},{j}↖{→},{k}↖{→})$.
$x$ est l'abscisse de ${v}↖{→}$.
$y$ est l'ordonnée de ${v}↖{→}$.
$z$ est la cote de ${v}↖{→}$.
Définition et propriété
Soient $(O,{i}↖{→},{j}↖{→},{k}↖{→})$ un repère de l'espace.
Pour tout point M, il existe un triplet $(x;y;z)$ de nombres réels tel que ${OM}↖{→}=x{i}↖{→}+y{j}↖{→}+z{k}↖{→}$.
Le triplet de réels $(x,y,z)$ est unique et s'appelle les coordonnées de M dans le repère $(O,{i}↖{→},{j}↖{→},{k}↖{→})$.
$x$ est l'abscisse de M.
$y$ est l'ordonnée de M.
$z$ est la cote de M.
Exemple
Reprenons encore une fois la figure du premier exemple:

Par lecture graphique, déterminer si les propositions suivantes sont vraies.
- $({DC}↖{→}$,${DH}↖{→}$,${DG}↖{→})$ est une base de l'espace.
- $({DC}↖{→}$,${DH}↖{→}$,${DA}↖{→})$ est une base de l'espace.
- $(A,{DA}↖{→}$,${FG}↖{→})$ est un repère du plan (DGA).
- $({DC}↖{→}$,${DH}↖{→}$,${DF}↖{→})$ est une base de l'espace.
- Le vecteur ${DA}↖{→}$ a pour coordonnées $(-1,1,-1)$ dans la base $({DC}↖{→}$,${DH}↖{→}$,${DF}↖{→})$
Corrigé
- C'est FAUX. $({DC}↖{→}$,${DH}↖{→}$,${DG}↖{→})$ n'est pas une base de l'espace car ces 3 vecteurs sont coplanaires (on a ${DG}↖{→}= {DC}↖{→}+{DH}↖{→}$).
- C'est VRAI. $({DC}↖{→}$,${DH}↖{→}$,${DA}↖{→})$ est une base de l'espace car ces 3 vecteurs ne sont pas coplanaires.
- C'est FAUX. $(A,{DA}↖{→}$,${FG}↖{→})$ n'est pas un repère du plan (DGA) car les vecteurs ${DA}↖{→}$ et ${FG}↖{→}$ sont colinéaires (ils sont même opposés).
- C'est VRAI. $({DC}↖{→}$,${DH}↖{→}$,${DF}↖{→})$ est une base de l'espace car ces 3 vecteurs ne sont pas coplanaires.
- C'est FAUX. On a: ${DF}↖{→}={DC}↖{→}+{DH}↖{→}+{DA}↖{→}$
Et donc: ${DF}↖{→}-{DC}↖{→}-{DH}↖{→}={DA}↖{→}$
Et par là, le vecteur ${DA}↖{→}$ a pour coordonnées $(-1,-1,1)$ dans la base $({DC}↖{→}$,${DH}↖{→}$,${DF}↖{→})$
Propriété
Soient $(O,{i}↖{→},{j}↖{→},{k}↖{→})$ un repère de l'espace.
Soient $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$ deux points de l'espace.
Le vecteur ${AB}↖{→}$ admet pour coordonnées $(x_B-x_A;y_B-y_A;z_B-z_A)$
Le milieu du segment $[AB]$ admet pour coordonnées $({x_A+x_B}/{2};{y_A+y_B}/{2};{z_A+z_B}/{2})$
Propriété
Soient $(O,{i}↖{→},{j}↖{→},{k}↖{→})$ un repère de l'espace.
Soient ${u}↖{→}(x;y;z)$ et ${V}↖{→}(x';y';z')$ deux vecteurs de l'espace, et soit $k$ un nombre réel.
Le vecteur ${u}↖{→}+{v}↖{→}$ admet pour coordonnées $(x+x';y+y';z+z')$
Le vecteur $k{u}↖{→}$ admet pour coordonnées $(kx,ky;kz)$
Exemple
Reprenons encore une fois la figure du premier exemple:

$(D$,${DC}↖{→}$,${DH}↖{→}$,${DA}↖{→})$ est un repère de l'espace.
- Donner (sans justifier) les coordonnées des points A, C, E, F, G et F .
- Montrer que $({CE}↖{→}$,${HC}↖{→}$,${GA}↖{→})$ est une base de l'espace.
Corrigé
- On obtient facilement:
A(0,0,1), C(1,0,0), E(0,1,1), F(1,1,1), G(1,1,0) et H(0,1,0) - On calcule: $x_E-x_C=0-1=-1$ $y_E-y_C=1-0=1$ $z_E-z_C=1-0=1$
Donc ${CE}↖{→}$ a alors pour coordonnées: $(-1,1,1)$
De même, on obtient: ${HC}↖{→}(1,-1,0)$, et ${GA}↖{→}(-1,-1,1))$
Pour prouver que $({CE}↖{→}$,${HC}↖{→}$,${GA}↖{→})$ est une base de l'espace, il suffit de vérifer que ${CE}↖{→}$, ${HC}↖{→}$ et ${GA}↖{→}$ sont linéairement indépendants.
$a{CE}↖{→}+b{HC}↖{→}+c{GA}↖{→}={0}↖{→}$ $⇔$ $\{\table -a+b-c=0;a-b-c=0; a+c=0$ $⇔$ $\{\table -a+b-c=0;a-b-c=0; a=-c$
$⇔$ $\{\table c+b-c=0;-c-b-c=0; a=-c$ $⇔$ $\{\table b=0;-c-0-c=0; a=-c$ $⇔$ $\{\table b=0;c=0; a=0$
Par conséquent: $a{CE}↖{→}+b{HC}↖{→}+c{GA}↖{→}={0}↖{→}$ implique que $a=b=c=0$,
et par là, ${CE}↖{→}$, ${HC}↖{→}$ et ${GA}↖{→}$ sont linéairement indépendants.
Et donc $({CE}↖{→}$,${HC}↖{→}$,${GA}↖{→})$ est une base de l'espace.