 Intégrales
Intégrales
I Cas des fonctions continues et positives
a. Intégrales et aires
Définition
Soit $f$ une fonction continue et positive sur un intervalle $[a;b]$.
Soit $C$ la courbe représentative de $f$ dans un repère orthogonal (les axes sont perpendiculaires).
$$∫_a^b f(t)dt$$ est l'aire (en unités d'aires) du domaine D délimité par la courbe $C$, l'axe des abscisses et les droites d'équations $x=a$ et $x=b$.
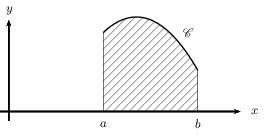
$∫_a^b f(t)dt$ se dit: "intégrale de $a$ à $b$ de $f(t)$ $dt$"
 Exemple
Exemple
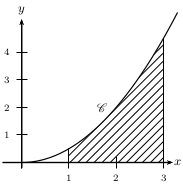
Soit $f$ définie sur $ℝ$ par $f(x)=0,5x^2$, de courbe représentative $C$ dans un repère orthogonal
(unités: 1 cm sur l'axe des abscisses, 0,5 cm sur l'axe des ordonnées)
On admet que $∫_1^3 f(t)dt=13/3≈4,333$.
Déterminer l'aire $A$ du domaine $D=${$M(x;y)$/$1≤x≤3$ et $0≤y≤f(x)$}.
Corrigé
La fonction $f$, dérivable, est donc continue.
De plus, il est évident que $f$ est positive sur $[1;3]$.
Donc $$A=∫_1^3 f(t)dt=13/3≈4,333$$.
L'aire du domaine $D$ vaut environ 4,333 unités d'aire.
$D$ est hachuré dans la figure ci-contre.
Calculons l'aire (en $cm^2$) d'une unité d'aire, c'est à dire celle d'un rectangle de côtés 1 unité (sur l'axe des abscisses) et 1 unité (sur l'axe des ordonnés).
Sa surface mesure: 1x0,5=0,5 $cm^2$.
Donc, une unité d'aire représente 0,5 $cm^2$.
Et comme 4,333x0,5=2,166, l'aire cherchée vaut environ 2,166 $cm^2$.
b. Intégrales et primitives
Propriété
Si $f$ est une fonction continue et positive sur un intervalle $[a;b]$.
Alors la fonction $F_a$ définie sur $[a;b]$ par $$F_a(x)=∫_a^x f(t)dt$$ est la primitive de $f$ qui s'annule en $a$.
Propriété
Soit $f$ une fonction continue et positive sur un segment $[a;b]$.
Soit F une primitive quelconque de $f$ sur I.
On a alors l'égalité:
$$∫_a^b f(t)dt=F(b)-F(a)$$
On note également: $$∫_a^b f(t)dt=[F(t)]_a^b$$
 Exemple
Exemple
Soit $f$ définie sur $ℝ$ par $f(x)=0,5x^2$.
Déterminer l'aire du domaine D délimité par la courbe $C_f$, l'axe des abscisses et les droites d'équations $x=1$ et $x=3$.
Corrigé
La fonction $f$, dérivable, est donc continue.
Elle est clairement positive sur $[1;3]$.
Donc l'aire cherchée est $∫_1^3 f(t)dt$.
Or, une primitive de $f$ est $F$, définie par $F(x)=0,5{x^3}/{3}$ sur $ℝ$.
Donc $$∫_1^3 f(t)dt=∫_1^3 0,5t^2dt=[F(x)]_1^3=[0,5{x^3}/{3}]_1^3$$
Soit: $$∫_1^3 f(t)dt=0,5{3^3}/{3}-0,5{1^3}/{3}=0,5(27/3-1/3)$$
Soit: $∫_1^3 f(t)dt=0,5 26/3=13/3≈4,333$.
L'aire est d'environ 4,333 unités d'aire.
II Cas des fonctions continues
a. Intégrales et primitives
Propriété
Toute fonction continue sur un intervalle admet des primitives.
Définition
Soit $f$ une fonction continue de signe quelconque sur un intervalle I contenant les réels $a$ et $b$.
Soit F une primitive quelconque de $f$ sur I.
Alors $∫_a^b f(t)dt$ est définie par l'égalité:
$$∫_a^b f(t)dt=F(b)-F(a)$$
On note également: $$∫_a^b f(t)dt=[F(t)]_a^b$$
On notera que la fonction $f$ peut être positive, ou négative, ou de signe variable, et que les réels $a$ et $b$ sont dans un ordre quelconque.
On notera également que, pour tout $x$ de I, $F_a(x)=∫_a^x f(t)dt$ est, comme au paragraphe I, la primitive de $f$ qui s'annule en $a$.
 Exemple
Exemple
$∫_5^2 -t^2dt=[-{t^3}/{3}]_5^2=-{2^3}/{3}-(-{5^3}/{3})=-{8}/{3}+{125}/{3}=39$
On notera qu'ici, la fonction $f(t)=-t^2$ est négative, et que 5>2.
$∫_5^x -t^2dt=-{t^3}/{3}+{125}/{3}$ est la primitive de $-t^2$ qui s'annule en $5$.
b. Valeur moyenne
Définition
Soit $f$ une fonction continue sur un intervalle $[a;b]$.
La valeur moyenne de $f$ sur $[a;b]$ est le nombre réel $$m=1/{b-a}∫_a^b f(t)dt$$ .
Propriété
Soit $f$ une fonction continue et positive sur un intervalle $[a;b]$, de valeur moyenne $m$ sur $[a;b]$.
Soit $C$ la courbe représentative de $f$ dans un repère orthogonal.
Le rectangle de côtés $m$ et $b-a$ a même aire que le domaine situé sous la courbe $C$.
 Exemple
Exemple
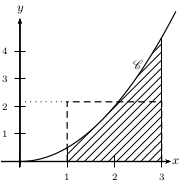
Soit $f$ la fonction de l'exemple précédent définie sur $ℝ$ par $f(x)=0,5x^2$.
Déterminer $m$, valeur moyenne de la fonction $f$ sur $[1;3]$.
Interpréter graphiquement.
Corrigé
$$m=1/{3-1}∫_1^3 f(t)dt$$ .
Or, on a vu dans l'exemple précédent que: $∫_1^3 f(t)dt≈4,333$.
Donc $$m≈1/{2}4,333≈2,166$$ .
Comme $f$ est positive, le rectangle de hauteur $2,166$ et de largeur $2$
a même aire que le domaine hachuré situé sous la courbe $C$.
c. Propriétés
Linéarité
Soit $f$ et $g$ deux fonctions continues sur un intervalle contenant les réels $a$ et $b$, et $k$ un nombre réel.
Alors: $$∫_a^b (f(t)+g(t))dt=∫_a^b f(t)dt+∫_a^b g(t)dt$$
et: $$∫_a^b (kf(t))dt=k∫_a^b f(t)dt$$ .
En particulier, on obtient: $$∫_a^b (f(t)-g(t))dt=∫_a^b f(t)dt-∫_a^b g(t)dt$$ .
Aire entre deux courbes
Soit $f$ et $g$ deux fonctions continues sur un intervalle $[a;b]$
Si $g≤f$ sur $[a;b]$,
alors $∫_a^b (f(t)-g(t))dt$ est l'aire du domaine situé entre les deux courbes $\C_f$ et $\C_g$ (quel que soit le signe des fonctions $f$ et $g$).
 Exemple
Exemple
On considère les fonctions $f(x)=\ln x+x^2$ et $g(x)=\ln x +x$ sur l'intervalle $\[1;2\]$.
Montrer qu'elles sont positives sur $\[1;2\]$, et que $g≤f$ sur $\[1;2\]$.
Le plan est rapporté à un repère orthogonal.
On admet que $$∫_1^2 (t^2-t)dt=7/6≈1,17$$
Déterminer alors l'aire $A$ entre les deux courbes.
Corrigé
$x^2$ est positif pour tout $x$.
$\ln x$ est positif pour tout $x$ supérieur ou égal à 1.
$x$ est positif pour tout $x$ supérieur ou égal à 0.
Donc, sur $\[1;2\]$, $x^2$, $\ln x$ et $x$ sont positifs,
et par là, $f$ et $g$ le sont.
Par ailleurs, $x≤x^2$ pour $x≥1$, et par là, $g≤f$ sur $\[1;2\]$.
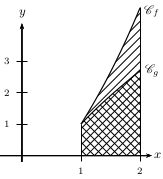
L'aire $A$ est la différence des deux aires sous les courbes:
$$A=∫_1^2 f(t)dt-∫_1^2 g(t)dt=∫_1^2 (f(t)-g(t))dt$$ (on aurait pu écrire directement $A=∫_1^2 (f(t)-g(t))dt$ car la positivité des fonctions n'est pas indispensable)
On a donc: $$A==∫_1^2 ((\ln t+t^2)-(\ln t+t)))dt=∫_1^2 (\ln t+t^2-\ln t-t)dt=∫_1^2 (t^2-t)dt$$
Soit: $$A=7/6≈1,17$$
Donc l'aire du domaine situé entre les deux courbes vaut environ 1,17 unités d'aire.
Notons qu'il vous aurait été difficile de calculer l'aire sous chacune des courbes car vous ne connaissez pas les primitives de la fonction $\ln$ (elles sont hors programme...).
Pour les curieux, voici le calcul de $$∫_1^2 (t^2-t)dt$$ à l'aide de primitive.
$$∫_1^2 (t^2-t)dt=[{t^3}/{3}-{t^2}/{2}]_1^2=(2^3/3-2^2/2)-(1^3/3-1^2/2)=8/3-4/2-1/3+1/2={16-12-2+3}/6=7/6≈1,17$$
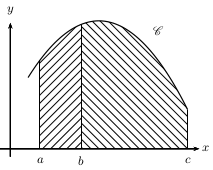
Relation de Chasles
Soit $f$ une fonction continue sur un intervalle contenant les réels $a$, $b$ et $c$.
Alors: $$∫_a^b f(t)dt+∫_b^c f(t)dt=∫_a^c f(t)dt$$ .
Si, de plus, $f$ est positive, et si $a$<$b$<$c$, alors cette propriété traduit l'additivité des aires:
l'aire sous la courbe entre $a$ et $c$ est la somme de l'aire sous la courbe entre $a$ et $b$ et de l'aire sous la courbe entre $b$ et $c$.
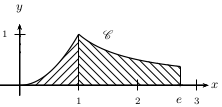
Exemple
On considère la fonction $f$ définie par $f(x)=x^2$ sur l'intervalle $\[0;1\]$ et par $f(x)=1/x$ sur l'intervalle $\]1;e\]$.
On admet que $$∫_0^1 f(t)dt=1/3$$ et $$∫_1^e f(t)d=1$$
Nous admettrons que $f$ est continue sur $\[0;e\]$.
Le plan est rapporté à un repère orthogonal.
Soit $D=\{M(x;y)$/$0≤x≤e$ et $0≤y≤f(x)\}$.
Déterminer l'aire $A$ de $D$.
Corrigé
Il est évident que $f$ est positive sur $[0;e]$.
Donc: $$A=∫_0^e f(t)dt=∫_0^1 f(t)dt+∫_1^e f(t)dt$$
Soit: $$A=1/3+1=4/3$$
Soit: $A≈1,33$ unités d'aire.
Pour les curieux, voici le calcul des 2 intégrales à l'aide de primitives.
On a: $$∫_0^1 f(t)dt=∫_0^1 t^2dt=[t^3/3]_0^1=(1^3/3-0^3/3)=1/3-0=1/3$$
et: $$∫_1^e f(t)dt=∫_1^e 1/tdt=[\ln t]_1^e=(\ln e-\ln 1)=1$$
Positivité
Soit $f$ une fonction continue sur un intervalle $\[a;b\]$.
Si $f≥0$ sur $\[a;b\]$, alors $$∫_a^b f(t)dt≥0$$ .
Si $f≤0$ sur $\[a;b\]$, alors $$∫_a^b f(t)dt≤0$$ .
Comparaison
Soient $f$ et $g$ deux fonctions continues sur un intervalle $\[a;b\]$.
Si $f≤g$ sur $\[a;b\]$, alors $$∫_a^b f(t)dt≤∫_a^b g(t)dt$$ .
Si, de plus, $f$ et $g$ sont positives, alors cette propriété traduit le fait que l'aire sous la courbe de $f$ est inférieure à celle située sous la courbe de $g$.
Exemple
Le plan est rapporté à un repère orthogonal.
On considère la fonction $f$ continue sur l'intervalle $\[1;2\]$ telle que $1/x^2≤f(x)≤1/x$ sur l'intervalle $\[1;2\]$.
On admet que $$∫_a^b 1/t^2dt=0,5$$ et $$∫_a^b 1/t dt=\ln 2$$
Déterminer un encadrement d'amplitude 0,2 de l'aire $A$ du domaine situé sous la courbe de $f$.
Corrigé
Comme $1/x^2≤f(x)≤1/x$ sur l'intervalle $\[1;2\]$,
on obtient: $$∫_a^b 1/t^2dt≤∫_a^b f(t)dt≤∫_a^b 1/t dt$$
Soit: $0,5≤A≤\ln 2$.
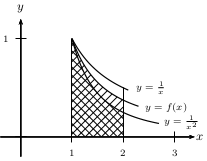
Comme $\ln 2≈0,69$, on obtient: $0,5≤A≤0,7$.
C'est un encadrement convenable.
Pour les curieux, voici le calcul des 2 intégrales à l'aide de primitives.
On a: $$∫_a^b 1/t^2dt=[{-1}/{t}]_1^2={-1}/{2}-{-1}/{1}=0,5$$
et: $$∫_a^b 1/t dt=[\ln t]_1^2=(\ln 2-\ln 1)=\ln 2$$
d. Intégration par parties
Intégration par parties
Soit I un intervalle contenant les réels $a$ et $b$.
Soit $u$ et $v$ deux fonctions dérivables sur I, dont les dérivées $u'$ et $v'$ sont également continues sur I.
Alors: $$∫_a^b u'(t)v(t) dt=[u(t)v(t)]_a^b-∫_a^b u(t)v'(t)dt$$ .
On note souvent: $∫_a^b u'v dt=[uv]_a^b-∫_a^b uv'dt$
Exemple
Calculer $∫_0^1 xe^x dx$
Corrigé
On ne connait pas de primitive de $xe^x$, mais on repère un produit. Une intégration par partie semble judicieuse.
On pose: $u'=e^x$ et $v=x$.
Par conséquent: $u=e^x$ convient. Et de plus, on a: $v'=1$
On obtient alors: $∫_0^1 xe^x dx=[e^x × x]_0^1-∫_0^1 e^x × 1dx$
Soit: $∫_0^1 xe^x dx=e^1 × 1-e^0 × 0-∫_0^1 e^x dx=e-∫_0^1 e^x dx$
Or: $∫_0^1 e^x dx=[e^x]_0^1=e^1-e^0=e-1$
Donc finalement: $∫_0^1 xe^x dx=e-e+1=1$
L'intégration par partie a remplacé le calcul de $∫_a^b u'v dt$ par celui de $∫_a^b uv'dt$.