 Fonction logarithme népérien
Fonction logarithme népérien
Définition et propriété
La fonction logarithme népérien, notée $\ln$, est la fonction définie sur $]0;+∞[$ qui,
à tout réel strictement positif $b$ associe l'unique solution de l'équation $e^x=b$.
Ainsi, pour tout réel $b$ strictement positif, pour tout réel $a$, $a=\ln b⇔ e^a=b$.
Et par là, on obtient, en particulier:
$\ln 1=0$ $\ln e=1$.
Propriété
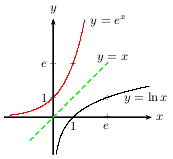
Dans un repère orthonormé, les courbes représentatives des fonction $\ln x$ et $e^x$ sont symétriques par rapport à la droite d'équation $y=x$.
Dérivées
La fonction $\ln x$ admet pour dérivée ${1}/{x}$ sur $]0;+∞[$. Ainsi: $(\ln x)'={1}/{x}$
Soit $u$ une fonction strictement positive sur un intervalle I.
La fonction $\ln u$ admet pour dérivée ${u'}/{u}$ sur I. Ainsi: $(\ln u)'={u'}/{u}$
Conséquence: Les fonctions $u$ et $\ln u$ ont même sens de variation sur I.
 Exemple
Exemple
Soit $f$ définie sur $]0;+∞[$ par $f(x)=7\ln x+3x$.
Montrer que $f\,'(x)={7+3x}/{x}$.
Corrigé
$f\,'(x)=7{1}/{x}+3={7}/{x}+{3x}/{x}={7+3x}/{x}$. Exemple
Exemple
Soit $f$ définie par $f(x)=3x-\ln (2x-1)$.
Déterminer le domaine de définition $\D_f$ de $f$.
Calculer $f\,'(x)$, puis montrer que $f$ admet pour minimum $2,5-\ln{2}/{3}$ sur $\D_f$.
Corrigé
$f(x)$ existe si et seulement si $2x-1\text">"0$, soit: $x\text">"0,5$. Donc $D_f=]0,5;+∞[$.
On pose $u=2x-1$, et donc $u'=2$.
Ici $f=3x-\ln u$, et par là $f\,'=3-{u'}/{u}$.
Donc $f\,'(x)=3-{2}/{2x-1}={3(2x-1)}/{2x-1}-{2}/{2x-1}={6x-3-2}/{2x-1}={6x-5}/{2x-1}$.
Le signe de $f\,'$ et le sens de variation de la fonction $f$ sont donnés ci-dessous.
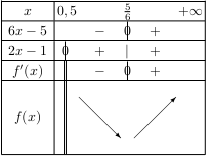
Et par là, $f$ admet pour minimum $f({5}/{6})=3×{5}/{6}-\ln (2×{5}/{6}-1)=2,5-\ln {2}/{3}$.
Propriétés
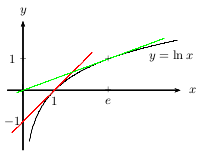
La fonction $\ln x$ est continue sur $]0;+∞[$.
$\ln x$ est strictement négative sur $]0;1[$.
$\ln x$ est strictement positive sur $]1;+∞[$.
La fonction $\ln x$ est strictement croissante.
Exemple
Soit $\C$ la courbe représentative de $\ln x$.
Déterminer une équation de $d_0$, tangente à $C$ en 1.
Déterminer une équation de $d_1$, tangente à $C$ en e.
Corrigé
Posons $f(x)=\ln x$. On a donc: $f\,'(x)={1}/{x}$.
$d_0$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
ici: $x_0=1$, $f(x_0)=\ln 1=0$, $f\,'(x_0)={1}/{1}=1$.
D'où l'équation: $y=0+1(x-1)$, soit: $y=x-1$.
Donc finalement, $d_0$ a pour équation: $y=x-1$ (elle est tracée en rouge sur le dessin de la propriété précédente).
$d_1$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
ici: $x_0=e$, $f(x_1)=\ln e=1$, $f\,'(x_1)={1}/{e}$.
D'où l'équation: $y=1+{1}/{e}(x-e)$, soit: $y=1+{1}/{e}x-1$, soit: $y={1}/{e}x$.
Donc finalement, $d_1$ a pour équation: $y={1}/{e}x$ (elle est tracée en vert sur le dessin de la propriété précédente).
Exemple
Sans calculatrice, donner le signe de $\ln 0,5$, de $\ln 1,9$.
Corrigé
$0,5\text"<"1$, et donc $\ln 0,5\text"<"0$.
$1,9\text">"1$, et donc $\ln 1,9\text">"0$.
Limites de référence
$\lim↙{x→+∞}\ln x=+∞$
$\lim↙{x→0}\ln x=-∞$ $\lim↙{x→0}x\ln x=0$
$\lim↙{x→+∞}{\ln x}/{x}=0$ $\lim↙{x→+∞}{\ln x}/{x^n}=0$ (pour $n∈\ℕ$ et $n\text">"0$)
$\lim↙{x→0}{\ln (1+x)}/{x}=1$
 Exemple
Exemple
Déterminer $\lim↙{x→+∞}\ln (x^2+1)+2{\ln x}/{x}$.
Déterminer $\lim↙{x→0}\ln ({1}/{x^2}+3)-\ln x+{\ln (1+x)}/{x}+x\ln x$.
Corrigé
On a $\lim↙{x→+∞}x^2+1=+∞$.
Or $\lim↙{y→+∞}\ln y=+∞$.
Donc $\lim↙{x→+∞}\ln (x^2+1)=+∞$.
D'autre part $\lim↙{x→+∞} 2{\ln x}/{x}=2×0=0$.
Donc finalement $\lim↙{x→+∞}\ln (x^2+1)+2{\ln x}/{x}=+∞$ (limite d'une somme).
On a $\lim↙{x→0}{1}/{x^2}=+∞$, et donc $\lim↙{x→0}{1}/{x^2}+3=+∞$.
Or $\lim↙{y→+∞}\ln y=+∞$.
Donc $\lim↙{x→0}\ln ({1}/{x^2}+3)=+∞$.
D'autre part $\lim↙{x→0}\ln x=-∞$, et par là $\lim↙{x→0}-\ln x=+∞$.
Enfin $\lim↙{x→0}{\ln (1+x)}/{x}=1$.
Et $\lim↙{x→0}x\ln x=0$.
Donc finalement $\lim↙{x→0}\ln ({1}/{x^2}+3)-\ln x+{\ln (1+x)}/{x}+x\ln x=+∞$ (limite d'une somme).
Propriétés
Pour tous nombres réels strictement positifs $a$ et $b$, pour tout entier relatif $p$, on a:
$\ln ab=\ln a+\ln b$ $\ln {a}/{b}=\ln a-\ln b$ $\ln a^p=p\ln a$ $\ln √a={1}/{2}\ln a$
Pour tous nombre réel $a$ , on a: $\ln (e^a)=a$
Pour tous nombre réel strictement positif $a$ , on a:
$e^{\ln a}=a$
Exemple
Simplifier les expressions suivantes: $A=3\ln 2-\ln4+\ln(e^{1,19})$ $B=\ln x^2-\ln x+e^{\ln3,7}$.
Corrigé
$A=3\ln 2-\ln4+\ln(e^{1,19})=\ln 2^3-\ln4+1,19=\ln8-\ln4+1,19$.
Soit: $A=\ln{8}/{4}+1,19=\ln2+1,19$.
$B=\ln x^2-\ln x+e^{\ln3,7}=\ln{x^2}/{x}+3,7=\ln x+3,7$.
Propriétés
Pour tous nombres réels strictement positifs $a$ et $b$, on a:
$\ln a\text"<"\ln b$ $ ⇔$ $ a\text"<"b$
et $\ln a=\ln b$ $ ⇔$ $ a=b$
 Exemple
Exemple
- Résoudre l'équation $\ln(x-2)=0$.
- Résoudre l'inéquation $\ln(-5x+3)-1≤0$.
- Résoudre l'inéquation $\ln(-5x+3)≤4$.
- Résoudre l'inéquation $e^(-4x)-7≤0$.
- Résoudre l'inéquation $5×0,98^n≤0,9$ où $n$ est un entier naturel.
Corrigé
-
On doit avoir $x-2\text">"0$, soit $x\text">"2$. Donc $\D_E=]2;+∞[$.
$\ln(x-2)=0⇔\ln(x-2)=\ln 1⇔x-2=1⇔x=3$.
Autre méthode: $\ln(x-2)=0⇔e^{\ln(x-2)}=e^0⇔x-2=1⇔x=3$.
Donc $\S=\{3\}$. Notons que 3 est bien dans $\D_E$ -
On doit avoir $-5x+3\text">"0$, soit $-5x\text">"-3$, soit $x\text"<"{-3}/{-5}$, soit $x\text"<"0,6$.
Donc $\D_E=]-∞;0,6[$.
(E)$⇔\ln(-5x+3)-1≤0⇔\ln(-5x+3)≤1$
Soit: (E) $⇔\ln(-5x+3)≤\ln e⇔-5x+3≤e$
Autre méthode: (E)$⇔e^{\ln(-5x+3)}≤e^1⇔-5x+3≤e$
Soit: (E)$⇔-5x≤e-3⇔x≥{e-3}/{-5}$
Donc $\S=[{e-3}/{-5};0,6[$. Notons que ${e-3}/{-5}≈0,06$. -
On doit avoir $-5x+3\text">"0$, soit $-5x\text">"-3$, soit $x\text"<"{-3}/{-5}$, soit $x\text"<"0,6$.
Donc $\D_E=]-∞;0,6[$.
$\ln(-5x+3)≤4⇔e^{\ln(-5x+3)}≤e^4⇔-5x+3≤e^4⇔-5x≤e^4-3⇔x≥{e^4-3}/{-5}$
Donc $\S=[{e^4-3}/{-5};0,6[$. Notons que ${e^4-3}/{-5}≈-10,32$. -
$\D_E=\R$
$e^(-4x)-7≤0⇔e^(-4x)≤7⇔\ln(e^(-4x))≤\ln 7⇔-4x≤\ln 7⇔x≥{\ln 7}/{-4}$.
Donc $\S=[{\ln 7}/{-4};+∞[$. Notons que ${\ln 7}/{-4}≈-0,49$. -
$\D_E$ est l'ensemble des entiers naturels.
(E)$⇔5×0,98^n≤0,9⇔0,98^n≤{0,9}/{5}⇔0,98^n≤0,18⇔\ln0,98^n≤\ln 0,18$
Soit: (E)$⇔n\ln0,98≤\ln 0,18$.
Soit: (E)$⇔n≥{\ln 0,18}/{\ln0,98}$.
Notons le changement de sens de l'inégalité car $\ln 0,98\text"<"0$.
On a: ${\ln 0,18}/{\ln0,98}≈84,88$.
Donc, finalement, $\S$ est l'ensemble des entiers supérieurs ou égaux à $85$.
Savoir faire
Comment résoudre les équations et les inéquations où apparait la fonction $\ln$ ou la fonction exponentielle?
En général, il suffit d'isoler le terme contenant la fonction problématique,
puis de composer chaque membre de l'équation ou de l'inéquation par la fonction réciproque.
(lire l'exemple ci-dessus)