 Primitives et équations différentielles
Primitives et équations différentielles
Définition
Résoudre l' équation différentielle $y\,'=f$ sur l'intervalle I, c'est déterminer toutes les fonctions $y$ dont la dérivée vaut $f$ sur I.
Une fonction solution de l' équation différentielle $y\,'=f$ s'appelle une primitive de $f$ sur I.
Une primitive de $f$ se note souvent $F$.
Exemple
Sur ℝ, la dérivée de la fonction $x^2$ est la fonction $2x$.
Donc $y=x^2$ est une fonction solution de l'équation différentielle $y\,'=2x$ sur ℝ.
On notera les abus de notation: $y$ à la place de $y(x)$ et $y\,'$ à la place de $y\,'(x)$.
On peut également dire que $F(x)=x^2$ est une primitive de la fonction $f(x)=2x$ sur ℝ.
A retenir
Pour montrer que $g$ est une primitive de $f$, il suffit de montrer que $g'=f$.
Propriété
Toute fonction $f$ continue sur un intervalle I admet une primitive F sur I.
Propriété
Soit F une primitive de $f$ sur un intervalle I.
Si $G=F+c$, où $c$ est une constante, alors $G$ est aussi une primitive de $f$.
Toute primitive de $f$ sur I est de la forme $F+c$, où $c$ est une constante.
 Exemple
Exemple
Déterminer la primitive G de $f(x)={-1}/{x^2}$ sur $]0;+∞[$ telle que $G(2)=3$.
Corrigé
Sur $]0;+∞[$, la dérivée de $1/x$ est ${-1}/{x^2}$.
Donc la fonction F définie par $F(x)={1}/{x}$ est une primitive de la fonction $f$ sur $]0;+∞[$
Donc toute primitive G de $f$ s'écrit sous la forme: $G(x)= F(x)+c$, où $c∈ℝ$.
On cherche donc une fonction $G$ définie par $G(x)={1}/{x}+c$ (où $c∈ℝ$) telle que $G(2)=3$.
Or: $G(2)=3 ⇔{1}/{2}+c=3 ⇔ c=3-0,5=2,5$.
Donc, la fonction G définie par $G(x)={1}/{x}+2,5$ sur $]0;+∞[$ est la primitive cherchée.
Primitives usuelles
Sur des intervalles convenables:
une primitive de $f(x)=k$ (où $k$ est un nombre réel) est $F(x)=kx$.
une primitive de $f(x)=x$ est $F(x)={x^2}/2$.
une primitive de $f(x)=1/{x^2}$ est $F(x)={-1}/x$.
une primitive de $f(x)=x^n$ est $F(x)={x^{n+1}}/{n+1}$ (où $n$ est un entier différent de 0 et de -1).
une primitive de $f(x)=1/√x$ est $F(x)=2√x$.
une primitive de $f(x)=e^x$ est $F(x)=e^x$.
une primitive de $f(x)=1/ x$ est $F(x)=\ln x$.
une primitive de $f(x)=\cos x$ est $F(x)=\sin x$.
une primitive de $f(x)=\sin x$ est $F(x)=-\cos x$.
une primitive de $f(x)=u' ×(v'o u)$ est $F=vo u$ .
Primitives particulières
Sur des intervalles convenables:
une primitive de $f(x)=u'u^n$ est $F(x)={1}/{n+1}u^{n+1}$ (où $n$ est un entier différent de 0 et de -1).
une primitive de $f(x)=u'e^u$ est $F(x)=e^u$.
une primitive de $f(x)={u'}/{u}$ est $F(x)=\ln u$.
une primitive de $f(x)={u'}/{u^2}$ est $F(x)={-1}/u$.
une primitive de $f(x)={u'}/{√u}$ est $F(x)=2√u$.
Primitives d'une somme et d'un produit par un nombre réel
Sur un intervalle I,
si $u$ et $v$ ont pour primitives respectives U et V, et si $k$ est un nombre réel,
alors $u+v$ a pour primitive $U+V$
et $ku$ a pour primitive $kU$.
Exemple
Déterminer les primitives F de $f(x)=50x^2+1/{2√x}+2xe^{x^2}$ sur $]0;+∞[$.
Corrigé
On a: $f=ku+v +w'e^w$ avec $k=50$, $u=x^2$, $v=1/{2√x}$, $w=x^2$ et $w'=2x$.
Suivant les conventions usuelles, on pose: $U={x^3}/{3}$, $V=√x$.
Donc une primitive convenable est $F=kU+V+e^w$, et par là: $F(x)=50{x^3}/{3}+√x+e^{x^2}$.
Donc, sur $]0;+∞[$, les primitives cherchées sont du type: $F(x)=50{x^3}/{3}+√x+e^{x^2} +c$, où $c$ est une constante.
A quoi servent les primitives ?
Elles sont la base du calcul intégral (voir chapitre intitulé Intégrales"). Elles permettent de résoudre certaines équations différentielles.
Equation différentielle $y' = ay$
Soit $a$ un réel fixé
L'équation différentielle $y' = ay$ sur ℝ admet pour solutions les fonctions $f_k$ définies par : $f_k(x) = k.e^{ax}$ (où $k$ est un réel), et ce sont les seules solutions.
Exemple
Les solutions de l'équation différentielle $y' = 0,3y$ sur $ ℝ$ sont les fonctions $f_k$ définies par : $f_k(x) = k.e^{0,3x}$ (où $k$ est un réel).
Voici les représentations graphiques de certaines solutions de l'équation différentielle $y' =0,3y$ sur ℝ.
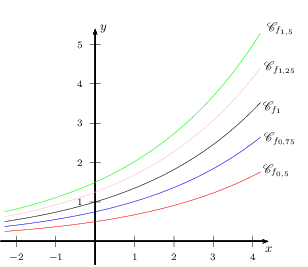
On constate graphiquement que la solution de l'équation différentielle $y' =0,3y$ sur $ℝ$ qui prend la valeur 1 en 2 est une fonction $f_k$ avec $k$ légèrement supérieur à 0,5.
Déterminer la formule donnant $f_k(x)$.
Corrigé
On a: $f_k(x) = k.e^{0,3x}$
Or $f_k(2)=1$. Donc $ k.e^{0,3×2}=1$. Et par là: $k={1}/{e^{0,6}}≈0,55$.
Donc la fonction cherchée est la fonction $f$ définie sur $ℝ$ par $f(x)={1}/{e^{0,6}}e^{0,3x}$
Equation différentielle $y' = ay+h$
Soit $a$ un réel fixé
Soit $h$ une fonction donnée
Les solutions de l'équation différentielle $y' = ay+h$ sur ℝ s'obtienne en déterminant une solution particulière de cette équation, et en lui ajoutant les solutions de l'équation différentielle $y' = ay$.
Exemple
On considère l'équation différentielle (E): $y' -3y=2e^{1-x}$ sur ℝ.
- Montrer que la fonction $g$ définie sur ℝ par $g(x) = -{1}/{2}e^{1 – x}$ est solution de l'équation (E).
- Montrer que $f$ est solution de (E) équivaut à $f – g$ solution de (E'): $y'=3y $.
- En déduire les solutions de (E).
Corrigé
-
On a: $g'(x)=-{1}/{2}(-e^{1 – x})={1}/{2}e^{1 – x}$
Donc: $g'(x)-3g(x)={1}/{2}e^{1 – x}+{3}/{2}e^{1 – x}$
Soit: $g'(x)-3g(x)=2e^{1 – x}$
Donc $g$ est solution de l'équation (E). - $f$ est solution de (E) si et seulement si $f'(x)-3f(x)=2e^{1 – x}$
si et seulement si $f'(x)-3f(x)=g'(x)-3g(x)$
si et seulement si $f'(x)-g'(x)=3(f(x)-g(x))$
si et seulement si $f – g$ solution de (E'): $y' = 3y $. - Or les solutions de $y' = 3y $ sont les fonctions $ke^{3x}$ (où k est un réel quelconque).
Par conséquent: $f(x)-g(x)=ke^{3x}$ (où k est un réel quelconque)
Et par là: $f(x)=g(x)+ke^{3x}$
Donc les fonctions $f(x)= -{1}/{2}e^{1 – x}+ke^{3x}$ (où k est un réel quelconque) sont les solutions de (E).
Un cas particulier de la propriété précédente est la propriété suivante.
Equation différentielle $y' = ay+b$
Soit $a$ un réel fixé non nul
Soit $b$ un réel fixé
L'équation différentielle $y' = ay+b$ sur ℝ admet pour solution particulière la fonction $f$ définie par : $f(x) = -{b}/{a}$.
L'équation différentielle $y' = ay+b$ sur ℝ admet pour solutions les fonctions $f_k$ définies par : $f_k(x) = k.e^{ax}-{b}/{a}$ (où $k$ est un réel), et ce sont les seules solutions.
Exemple
Déterminer les solutions de l'équation différentielle (E): $5y' -2y=3$ sur ℝ.
Corrigé
On a: (E) $⇔$ $y'={2}/{5}y+{3}/{5}$
L'équation différentielle (E) sur ℝ admet pour solution particulière la fonction $f$ définie par : $f(x) = -{3}/{5}×{5}/{2}=-{3}/{2}$.
L'équation différentielle (E) sur ℝ admet pour solutions les fonctions $f_k$ définies par : $f_k(x) = k.e^{{2}/{5}x}-{3}/{2}$ (où $k$ est un réel), et ce sont les seules solutions.
A quoi servent les équations différentielles ?
Elles sont la base de la plupart des modèles utilisés en physique, qui, sans elles, n'existerait pas...