 Sommes de variables aléatoires
Sommes de variables aléatoires
Voici tout d'abord un rappel du cours de première.
Définitions
Une variable aléatoire réelle $X$ sur l'univers $Ω$ d'une expérience aléatoire est une application de $Ω$ sur $\ℝ$.
Soit $x$ une valeur prise par la variable aléatoire $X$.
L'événement "$X=x$" est l'ensemble des événements $e_j$ de $Ω$ tels que $X(e_j)=x$.
L'événement "$X≤ x$" est l'ensemble des événements $e_j$ de $Ω$ tels que $X(e_j)≤ x$.
On définit de même les événements "$X$<$x$" , "$X≥x$" et "$X$>$x$"
La loi de probabilité de X est la probabilité qui, à toute valeur $x$ prise par X, associe la probabilité $p(X=x)$.
La variable aléatoire , de valeurs $x_i$, de probabilités $p_i$ pour $i$ entre 1 et $n$,
admet pour espérance le réel, noté $E(X)$, défini par
$E(X)=p_1x_1+p_2x_2+...+p_nx_n$.
$E(X)$ représente la valeur moyenne espérée de X sur un grand nombre d'expériences.
La variance de X, notée $V(X)$, est définie par $V(X)=p_1(x_1-E(X))^2+p_2(x_2-E(X))^2+...+p_n(x_n-E(X))^2$.
On remarque que $V(X)=E((X-E(X))^2)$.
Formule de König-Huygens $V(X)=E(X^2)-(E(X))^2$
L'écart-type, noté $σ$, de la variable aléatoire X est défini par
$σ=√ {V(X)}$.
L'écart-type mesure la dispersion des valeurs prises par X autour de son espérance.
Et voici ci-dessous le cours de terminale.
I Variables aléatoires et opérations
Définition
Soient X et Y deux variables aléatoires définies sur le même univers $Ω$.
La somme $X+Y$ est la variable aléatoire qui, à tout événement $e_j$ de $Ω$ associe le réel $X(e_j)+Y(e_j)$.
Et si $a$ est un réel, alors le produit $aX$ est la variable aléatoire qui, à tout événement $e_j$ de $Ω$ associe le réel $aX(e_j)$.
Exemple
On tire 2 jetons successivement d'une urne contenant les jetons 1, 2 et 3.
Soit X le numéro du premier jeton, et Y le numéro du second jeton.
Soit Z=X+Y la variable aléatoire donnant la somme des 2 numéros.
Soit C=3Z la variable aléatoire donnant le triple de la somme des 2 numéros.
Déterminer les lois de X, de Y, de Z et de C.
Corrigé
arbre pondéré:
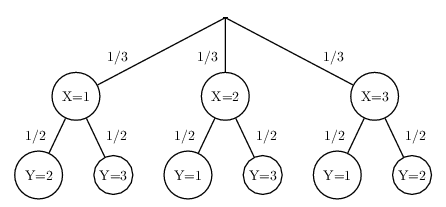
On a: $X( Ω)=\{1, 2, 3\}$
Et: $p(X=1)=p(X=2)=p(X=3)={1}/{3}$
On a: $Y( Ω)=\{1, 2, 3\}$
Et, en appliquant la formule des probabilités totales, on a:
$p(Y=1)=p(X=1)×p_{X=1}(Y=1)+p(X=2)×p_{X=2}(Y=1)+p(X=3)×p_{X=3}(Y=1)$
Soit: $p(Y=1)={1}/{3}×0+{1}/{3}×{1}/{2}+{1}/{3}×{1}/{2}={1}/{3}$
De même, on obtient: $p(Y=2)={1}/{3}$ et $p(Y=3)={1}/{3}$
On a: $Z( Ω)=\{3, 4, 5\}$
On note que: $(Z=3)=((X=1)∩(Y=2))∪((X=2)∩(Y=1))$.
Et par là: $p(Z=3)=p(X=1)×p_{X=1}(Y=2)+p(X=2)×p_{X=2}(Y=1)={1}/{3}×{1}/{2}+{1}/{3}×{1}/{2}={1}/{3}$
De même: $p(Z=4)=p(X=1)×p_{X=1}(Y=3)+p(X=3)×p_{X=3}(Y=1)={1}/{3}$
Et enfin: $p(Z=5)=1-p(Z=3)-p(Z=4)={1}/{3}$
On obtient facilement: $C( Ω)=\{9, 12, 15\}$
Et $p(C=9)=p(Z=3)={1}/{3}$, $p(C=12)=p(Z=4)={1}/{3}$ et $p(C=15)=p(Z=5)={1}/{3}$
Linéarité de l'espérance
Soient X et Y deux variables aléatoires définies sur le même univers $Ω$.
Soit $a$ un réel fixé.
On a:
$E(X+Y)=E(X)+E(Y)$ et $E(aX)=aE(X)$
Exemple
1. Reprendre l'exemple précédent et déterminer les espérances de X et de Y.
En déduire celle de Z.
2. Les deux tirages sont utilisés à chaque tour d'un jeu pour faire avancer une pièce. Cette dernière avance d'un nombre de cases C égal au triple de Z.
Déterminer l'espérance de la variable aléatoire C. Interpréter le résultat obtenu.
Corrigé
1. On a: $E(X)=p(X=1)×1+p(X=2)×2+p(X=3)×3={1}/{3}×1+{1}/{3}×2+{1}/{3}×3=2$
De même: $E(Y)=p(Y=1)×1+p(Y=2)×2+p(Y=3)×3={1}/{3}×1+{1}/{3}×2+{1}/{3}×3=2$
Par conséquent, comme $Z=X+Y$, on a: $E(Z)=E(X)+E(Y)=2+2=4$
2. On a: $C=3Z$, et donc $E(C)=3×E(Z)=3×4=12$
En moyenne, sur un grand nombre de tours, on peut espérer que la pièce avance 12 cases.
Propriété
On se place dans le cadre d'une succession de 2 épreuves indépendantes.
Si X est une variable aléatoire associée à la première épreuve, et Y une variable aléatoire associée à la seconde épreuve, alors on dit que les variables aléatoires X et Y sont indépendantes,
et on a la relation d'additivité suivante: $V(X+Y)=V(X)+V(Y)$.
Exemple
Reprendre encore l'exemple précédent et déterminer les variances de X, de Y et de Z.
A-t-on $V(X+Y)=V(X)+V(Y)$? Pourquoi?
Corrigé
On a: $V(X)=E((X−E(X))^2)=p(X=1)×(1-2)^2+p(X=2)×(2-2)^2+p(X=3)×(3-2)^2={1}/{3}×1+{1}/{3}×0+{1}/{3}×1={2}/{3}$
De même, on obtient: $V(Y)={2}/{3}$
Et: $V(Z)=E((Z−E(Z))^2)=p(Z=3)×(3-4)^2+p(Z=4)×(4-4)^2+p(Z=5)×(5-4)^2={1}/{3}×1+{1}/{3}×0+{1}/{3}×1={2}/{3}$
On a: $Z=X+Y$, et pourtant: $V(Z)≠V(X)+V(Y)$
En effet, les deux tirages n'étant pas indépendants, les variables aléatoires X et Y ne sont pas indépendantes.
Propriété
Soient X une variable aléatoire et $a$ un réel fixé.
On a:
$V(aX)=a^2V(X)$
Exemple
Reprendre une fois de plus l'exemple précédent et déterminer la variance de C.
Corrigé
On a: $V(C)=V(3Z)=3^2×V(Z)=9×{2}/{3}=6$
II Espérance et variance d'une loi binomiale
Propriété
Si $X$ suit une loi de Bernoulli de paramètre $p$, alors:
son espérance est: $E(X)=p$
sa variance est: $V(X)=p(1-p)$
son écart-type est: $σ(X)=√ {p(1-p)}$
Propriété
La loi binomiale, de paramètres $n$ et $p$, est la loi de probabilité d'une variable aléatoire X telle que :
$X=Y_{1}+Y_{2}+... +Y_{n}$
où $Y_{1}$,$Y_{2}$,... ,$Y_{n}$, sont des variables aléatoires indépendantes de loi de Bernoulli de même paramètre $p$.
Pour chaque $k$ entier entre 1 et $n$, $Y_{k}$ vaut 1 en cas de succès et 0 en cas d'échec à la $k.ième$ expérience. La variable X dénombre bien le nombre total de succès.
Conséquence
Si $X$ suit une loi binomiale de paramètre $n$ et $p$, alors:
son espérance est: $E(X)=np$
sa variance est: $V(X)=np(1-p)$
son écart-type est: $σ(X)=√ {np(1-p)}$
Exemple
On pose: $X=B(100;0,41)$ et $Y=B(50;0,78)$
Calculer les espérances et les variances de X et Y. Comparer ces variables aléatoires.
Corrigé
$E(X)=100×0,41=41$ $E(Y)=50×0,78=39$
Ces valeurs sont proches. En moyenne, sur un grand nombre d'expériences, les valeurs prises par ces variables aléatoires seront sans doute proches.
$V(X)=100×0,41×(1-0,41)=24,19$ $V(Y)=50×0,78×(1-0,78)=8,58$
La variance de X est environ trois fois plus grande que celle de Y. Le risque que la variable aléatoire s'éloigne de sa moyenne est beaucoup plus grand pour X que pour Y.
III Echantillons
Définition
Un échantillon aléatoire de taille $n$ d'une loi de probabilité est une liste de variables aléatoires indépendantes identiques ($X_1$, $X_2$,...,$X_n$) suivant cette loi.
Une liste ($x_1$, $x_2$,..., $x_n$) de valeurs prises par les variables aléatoires $X_i$ est une réalisation de l'échantillon.
Exemple 1
On appelle X la variable aléatoire donnant le résultat du lancer d'un dé.
On jette alors ce dé 10 fois de suite. Et on nomme $X_i$ la variable aléatoire donnant le résultat du i-ème lancer (pour $i$ entre 1 et 10).
Les lancers étant indépendants, la liste ($X_1$, $X_2$,...,$X_{10}$) est un échantillon aléatoire de taille $10$ de la loi de probabilité de X.
Et par exemple, la liste (2, 2, 5, 6, 1, 2, 4, 3, 6, 1) est une réalisation possible de cet échantillon.
Exemple 2
Une usine fabrique des médicaments sous forme de comprimés. On prélève 500 comprimés choisis au hasard parmi la production journalière, qui est de 1 000 000 de comprimés.
On considère la liste de variables aléatoires ($X_1$, $X_2$,...,$X_{500}$), telle que $X_i$ vaut 1 si le i-ème comprimé est conforme au cahier des charges,
et 0 sinon.
La production journalière est beaucoup plus grande que la taille de la liste.
Par conséquent, les prélèvements peuvent être assimilés à des tirages avec remise, et par là, les $X_i$ peuvent être considérées comme indépendantes et de même loi X.
La liste peut donc être assimilée à un échantillon aléatoire de taille 500 de la loi de probabilité de X.
Propriété
Soit ($X_1$, $X_2$,...,$X_n$) un échantillon de la loi de probabilité de la variable aléatoire X.
Soit la somme: $S_n=X_1+X_2+...+X_n$
Soit la moyenne: $M_n={S_n}/{n}$
On a alors:
$E(S_n)=n×E(X)$
$V(S_n)=n×V(X)$
$σ(S_n)=√{n}×σ(X)$
Et:
$E(M_n)=E(X)$
$V(M_n)={V(X)}/{n}$
$σ(M_n)={σ(X)}/{√{n}}$
Exemple
1. On reprend l'exemple 1 précédent.
Déterminer $E(X)$ et $V(X)$
2. Soit ($X_1$, $X_2$,...,$X_{10}$) un échantillon aléatoire de la loi de probabilité de X.
On pose: $S=X_1+X_2+...+X_{10}$ et: $M={S}/{10}$
Déterminer $E(S)$ et $V(S)$
Déterminer $E(M)$. Interpréter ce résultat.
Déterminer $V(M)$. La comparer à $V(X)$
3. Soit ($X_1$, $X_2$) un échantillon aléatoire de la loi de probabilité de X.
On pose: $S=X_1+X_2$ et: $M={S}/{2}$
On obtient facilement $E(M)=3,5$ et $V(M)=1,46$.
Et on peut alors constater que le risque que M soit loin de 3,5 est beaucoup plus faible que celui que X soit loin de 3,5.
Vérifions le dans un cas particulier.
Déterminer $p(|X-3,5|\text"<" 1)$ et $p(|M-3,5|\text"<" 1)$. Conclure.
Corrigé
1. On a:
$E(X)={1}/{6}×1+{1}/{6}×2+{1}/{6}×3+{1}/{6}×4+{1}/{6}×5+{1}/{6}×6={1}/{6}×(1+2+...+6)={1}/{6}×({6×7}/{2})=3,5$
$V(X)={1}/{6}×(1-3,5)^2+{1}/{6}×(2-3,5)^2+{1}/{6}×(3-3,5)^2+{1}/{6}×(4-3,5)^2+{1}/{6}×(5-3,5)^2+{1}/{6}×(6-3,5)^2={17,5}/{6}≈2,92$
2. On a:
$E(S)=10×E(X)=10×3,5=35$
$V(S)=10×V(X)=10×{17,5}/{6}≈29,2$
$E(M)=E(X)=3,5$
Sur un grand nombre d'échantillons, on peut espérer que la moyenne des 10 résultats par échantillon vaut, en moyenne, 3,5.
Le fait que $E(X)$ et $E(M)$ soient égaux est une évidence.
En effet, sur un grand nombre de lancers, la moyenne de ces lancers est problablement très proche de $E(X)$. Le groupement des lancers par séries de 10 ne change rien à la moyenne globale.
$V(M)={V(X)}/{10}≈{2,92}/{10}≈0,29$
La variance de la moyenne M est 10 fois plus faible que celle de X.
Et comme X et M ont la même espérance égale à 3,5, cela traduit le risque que M soit loin de 3,5 est beaucoup plus faible que celui que X soit loin de 3,5.
Cela est conforme à l'intuition, et traduit le fait qu'il est plus probable que la moyenne de 10 lancers soit proche de 3,5 que le résultat d'un seul lancer le soit.
3. $p(|X-3,5|\text"<"1)=p(X=3$ ou $X=4)={2}/{6}≈0,33$
On a: $|M-3,5|\text"<"1$ $ ⇔$ $M=3$ ou $M=3,5$ ou $M=4$
Or $M=3$ $ ⇔$ ($X_1=5$ et $X_2=1$) ou ($X_1=4$ et $X_2=2$) ou ... ou ($X_1=1$ et $X_2=5$)
Cela concerne donc 5 événements élémentaires.
De même, $M=3,5$ concerne 6 événements élémentaires.
Et $M=4$ concerne 5 événements élémentaires.
Les septiques peuvent faire un tableau des 36 couples de lancers de dés et des moyennes associées.
Par conséquent, sur les 36 lancers de 2 dés possibles, seuls 16 vérifient $|M-3,5|\text"<"1$.
Donc: $p(|M-3,5|\text"<"1)={16}/{36}≈0,44$
On constate que $p(|M-3,5|\text"<"1)$ est plus important que $p(|X-3,5|\text"<"1)$, ce qui cohérent avec le fait que $V(M)$ est plus faible que $V(X)$.
Exemple
1. On reprend l'exemple 2 précédent.
On suppose que $90\%$ des comprimés sont conformes au cahier des charges.
Déterminer $E(X)$ et $V(X)$
2. Soit ($X_1$, $X_2$,...,$X_{10}$) un échantillon aléatoire de la loi de probabilité de X.
On pose: $S=X_1+X_2+...+X_{10}$ et: $M={S}/{10}$
Donner la nature et les paramètres de la variable aléatoire S.
Déterminer $E(S)$ et $V(S)$
Déterminer $E(M)$. Interpréter ce résultat.
Déterminer $V(M)$. La comparer à $V(X)$
Corrigé
1. $X$ vaut 1 si le comprimé est conforme au cahier des charges,
et 0 sinon.
Et on a: $p(X=1)=0,90$.
X suit donc une loi de Berboulli de paramètre $p=0,90$.
On a:
$E(X)=p=0,90$
$V(X)=p(1-p)=0,90×0,10=0,09$
2. $X_{1}$,$X_{2}$,... ,$X_{500}$, sont des variables aléatoires indépendantes de loi de Bernoulli de même paramètre $p=0,90$.
Pour chaque $k$ entier entre 1 et $500$, $X_{k}$ vaut 1 en cas de succès et 0 en cas d'échec au $k$-ième prélèvement.
La variable S dénombre le nombre total de succès.
Par conséquent, S suit la loi binomiale de paramètres $n=500$ et $p=0,90$.
On a:
$E(S)=n×p==500×0,90=450$ (on retrouve le fait que $E(S)=500×E(X)$)
$V(S)=n×p×(1-p)=500×0,90×0,10=45$ (on retrouve le fait que $V(S)=500×V(X)$)
$E(M)=E(X)=0,90$
Sur un grand nombre d'échantillons de 500, on peut espérer que le pourcentage de prélèvements conforme par échantillon vaut, en moyenne, $90\%$.
Le fait que $E(X)$ et $E(M)$ soient égaux est une évidence.
En effet, sur un grand nombre de prélèvements, le pourcentage de prélèvements conforme est problablement très proche de $90\%$. Le groupement des prélèvements par séries de 500 ne change rien à la moyenne globale.
$V(M)={V(X)}/{500}={0,09}/{500}=1,8×10^{-4}$
La variance de la moyenne M est 500 fois plus faible que celle de X.
Et comme X et M ont la même espérance égale à 0,90, cela traduit le risque que M soit loin de 0,90 est beaucoup plus faible que celui que X soit loin de 0,90.
Cela est conforme à l'intuition. Pour faire simple, dire que X est loin de 0,90, cela signifie que l'échantillon est non conforme;
et dire que M est loin de 0,90, cela signifie que de trop nombreux prélèvements sont non conformes, ce qui est beaucoup moins probable qu'un seul prélèvement soit non conforme. La répétition "gomme" le hasard...