 Suites
Suites
Rappels de première
Une suite $(u_n)$ est arithmétique de raison $a$ si et seulement si
pour tout naturel $n$, $u_{n+1}=u_n+a$.
(ici, la suite est donnée par une formule de récurrence)
$(u_n)$ est arithmétique de raison $a$ si et seulement si
pour tout naturel $n$, $u_{n}=u_0+na$.
(ici, la suite est donnée par une formule explicite)
Pour tout entier naturel $n$, on a: $1+2+...+n={n(n+1)}/{2}$.
Une suite $(u_n)$ est géométrique de raison $q$ si et seulement si
pour tout naturel $n$, $u_{n+1}=u_n× q$.
(ici, la suite est donnée par une formule de récurrence)
$(u_n)$ est géométrique de raison $q$ si et seulement si
pour tout naturel $n$, $u_{n}=u_0× q^n$.
(ici, la suite est donnée par une formule explicite)
Pour tout réel $q$ (avec $q≠1$),on a: $1+q+q^2+...+q^n={1-q^{n+1}}/{1-q}$.
Savoir faire
Pour montrer qu'une suite $(u_n)$ est géométrique de raison $q$, on essaie en général de prouver la relation de récurrence $u_{n+1}=u_n× q$.
Mais, si cela semble difficile, on essaie alors de prouver la relation explicite $u_{n}=u_0× q^n$.
Quelle que soit la méthode, les relations doivent être vérifiées pour tout naturel $n$.
Il ne faut pas se contenter de faire quelques vérifications avec des valeurs de $n$ particulières!
A retenir
Une variation régulière de $a$ est associée à une suite arithmétique de raison $a$.
Une augmentation régulière de $t\%$ est associée à une suite géométrique de raison $1+t\%$.
Une baisse régulière de $t\%$ est associée à une suite géométrique de raison $1-t\%$.
I Limites infinies
Limite infinie
La suite $(u_n)$ a pour limite $+∞$ quand $n$ tend vers $+∞$ lorsque
tout intervalle du type $[A;+∞[$ (où $A$ est un réel) contient tous les termes $u_n$
de la suite à partir d'un certain rang.
On note $\lim↙{n→+∞}u_n=+∞$ La suite $(u_n)$ a pour limite $-∞$ quand $n$ tend vers $+∞$ lorsque
tout intervalle du type $]-∞;A]$ (où $A$ est un réel) contient tous les termes $u_n$
de la suite à partir d'un certain rang.
On note $\lim↙{n→+∞}u_n=-∞$
Exemple
Soit $u$ la suite définie par $u_n=3n^2-5$ pour tout naturel $n$.
Représenter graphiquement $(u_n)$ pour $n$ entre 0 et 5.
Soit $A=30$. Déterminer graphiquement $n_A$, plus petit naturel à partir duquel l'intervalle $[A;+∞[$ contient tous les termes $u_n$.
Montrer que $\lim↙{n→+∞}u_n=+∞$ en utilisant la définition d'une limite infinie (question non exigible).
Corrigé
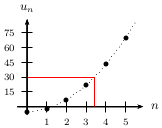
Graphiquement, on note que, pour A=30, $n_A=4$.
A partir de $n=4$, tous les $u_n$ sont supérieurs à $30$.
Soit $A$ un réel quelconque.
$u_n\text">"A⇔3n^2-5\text">"A⇔n^2\text">"{A+5}/{3}$.
Si $A\text"<"-5$, alors ${A+5}/{3}\text"<"0$, et comme le carré $n^2$ est positif ou nul,
l'inégalité précédente est toujours vraie. Dans ce cas, on pose $n_A=0$.
Par exemple, pour $A=-12$, on a $n_A=0$.
Sinon, $u_n\text">"A$ $⇔$ $n\text">"√{{A+5}/{3}}$. Dans ce cas, on pose $n_A=n_0$,
où $n_0$ est le plus petit naturel strictement supérieur à $√{{A+5}/{3}}$,
Par exemple, pour $A=30$, on a $n_A=4$.
Finalement, quel que soit $A$, l'intervalle $[A;+∞[$ contient tous les termes $u_n$ à partir du rang $n_A$.
Et par là: $\lim↙{n→+∞}u_n=+∞$.
Limites de référence
$\lim↙{n→+∞}n=+∞$ $\lim↙{n→+∞}n^2=+∞$ $\lim↙{n→+∞}n^3=+∞$ $\lim↙{n→+∞}√{n}=+∞$
Les plus curieux peuvent aussi apprendre que: $\lim↙{n→+∞}n^k=+∞$ (pour $k∈\ℕ$ et $k\text">"0$)
et: $\lim↙{n→+∞}e^n=+∞$
II Limites finies
Limite finie
La suite $(u_n)$ a pour limite $l$ quand $n$ tend vers $+∞$ lorsque tout intervalle ouvert contenant $l$ contient tous les termes $u_n$ de la suite à partir d'un certain rang.
On note $\lim↙{n→+∞}u_n=l$
On dit que la suite converge vers $l$.
Exemple
Soit $(u_n)$ la suite définie par $u_n=3+{1}/{n}$ pour tout naturel $n$ non nul.
Montrer que $\lim↙{n→+∞}u_n=3$ en utilisant la définition d'une limite finie (question non exigible).
Corrigé
Soit $]3-a;3+b[$ un intervalle ouvert quelconque contenant 3 (avec $a$ et $b$ strictement positifs).
$u_n∈]3-a;3+b[⇔3-a\text"<"u_n\text"<"3+b⇔3-a\text"<"3+{1}/{n}\text"<"3+b$.
Soit: $u_n∈]3-a;3+b[⇔-a\text"<"{1}/{n}\text"<"b$.
L'inégalité de gauche est toujours vraie car ${1}/{n}$ est strictement positif.
Donc: $u_n∈]3-a;3+b[⇔{1}/{n}\text"<"b⇔{1}/{b}\text"<"n$.
Notons que l'inégalité a conservé son sens car $n$ et $b$ sont strictement positifs.
On note alors $n_A$ le plus petit naturel strictement supérieur à ${1}/{b}$.
Finalement, quel que soient $a$ et $b$ strictement positifs,
l'intervalle ouvert $]3-a;3+b[$ contient tous les termes $u_n$ à partir du rang $n_A$.
Par exemple, l'intervalle $]2,8;3,1[$ (qui correspond à $a=0,2$ et $b=0,1$) contient tous les termes $u_n$ à partir du rang $11$.
Et par là: $\lim↙{n→+∞}u_n=3$.
Propriétés
La limite d'une suite est unique.
Si $\lim↙{n→+∞}u_n$ existe, alors $\lim↙{n→+∞}u_n=\lim↙{n→+∞}u_{n+1}$
Suite stationnaire
Soit $l$ un nombre réel; si $u_n=l$ à partir d'un certain rang, alors $\lim↙{n→+∞}u_n=l$.
Limites de référence
$\lim↙{n→+∞}{1}/{n}=0$ $\lim↙{n→+∞}{1}/{n^2}=0$ $\lim↙{n→+∞}{1}/{n^3}=0$ $\lim↙{n→+∞}{1}/{\√{n}}=0$
Les plus curieux peuvent aussi apprendre que: $\lim↙{n→+∞}{1}/{n^k}=0$ (pour $k∈\ℕ$ et $k\text">"0$)
et: $\lim↙{n→+∞}e^{-n}=0$
Limite de $(q^n)$
Si $q$>$1$, alors $\lim↙{n→+∞}(q^n)=+∞$.
Si $q=1$, alors $\lim↙{n→+∞}(q^n)=1$.
Si $-1$<$q$<$1$, alors $\lim↙{n→+∞}(q^n)=0$.
Si $q≤-1$, alors la suite $(q^n)$ n'a pas de limite.
Définition
La suite $(u_n)$ diverge lorsqu'elle a une limite infinie ou lorsqu'elle n'a pas de limite.
III Opérations
Opérations
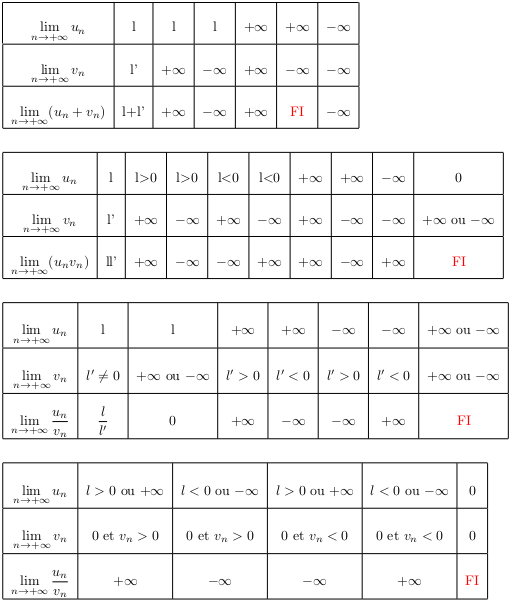
La détermination de la limite d'une somme, d'un produit ou d'un quotient de 2 suites est intuitive,
et vérifie les tableaux ci-dessous.
Retenir essentiellement les formes indéterminées (notées FI), à traiter cas par cas
(voir troisième série d'exemples ci-dessous).
Astuce
Dans une expression, toute constante peut être considérée comme une suite stationnaire, dont la limite est elle-même.
 Exemple
Exemple
Une somme de 1000 euros est placée à intérêts composés au taux de 0,2% par mois.
Soit $(u_n)$ le capital disponible au bout de $n$ mois.
- Exprimer $u_{n+1}$ en fonction de $u_n$ pour tout entier naturel $n$.
En déduire la nature de $(u_n)$.
Donner alors une formule explicite donnant $u_n$ en fonction de $n$ pour tout entier naturel $n$. - Déterminer $\lim↙{n→+∞}u_n$.
- Donner le sens de variation de $(u_n)$.
-
Soit A un nombre donné quelconque. Il existe une valeur de $n$ à partir de laquelle tous les termes $u_n$ sont supérieurs à A. Pourquoi?
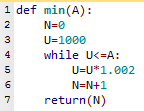
Ecrire l'algorithme d'une fonction d'un nombre A donné, appelée min(A), qui renvoie le plus petit rang $n_0$ à partir duquel $u_n$ est supérieur à A.
Que renvoie cette fonction pour A=1100?
Pourquoi votre algorithme fournit-il effectivement le plus petit $n_0$ convenable? - Ecrire en PYTHON un programme convenable pour la fonction min(A)
Corrigé
- $u_{n+1}=u_n+{0,2}/{100}u_n=(1+0,002)u_n=1,002u_n$ (pour tout entier naturel $n$).
Donc $(u_n)$ est géométrique de raison 1,002.
Donc $u_n=1,002^nu_0=1,002^n×1000$ (pour tout entier naturel $n$). - $1,002\text">"1$, donc $\lim↙{n→+∞}1,002^n=+∞$.
Par ailleurs, $\lim↙{n→+∞}1000=1000$. (cette ligne est souvent omise)
Et comme 1000>0, on obtient $\lim↙{n→+∞}u_n=+∞$. - $1,002\text">"1$, donc $(1,002^n)$ est strictement croissante (voir cours de première).
Et comme 1000>0, $(1,002^n×1000)$ est strictement croissante (voir cours de première).
Donc $(u_n)$ est strictement croissante. - Il existe une valeur de $n$ à partir de laquelle tous les termes $u_n$ sont supérieurs à A car $\lim↙{n→+∞}u_n=+∞$.
Une fonction convenable:
définition de la fonction min(A)
N $←$ 0
U ← 1000
Tant que U$≤$A
U $←$ Ux1,002
N $←$ N+1
Fin du Tant que
La valeur renvoyée est N
Pour A=1100, la fonction renvoie 48 (c'est la valeur de $n_0$).
La fonction fournit effectivement le plus petit $n_0$ convenable car $(u_n)$ est croissante. - Voici un programme convenable pour la fonction min(A)
 Exemples
Exemples
- Soit $(u_n)$ la suite définie par $u_n=(3n^2+n-5)√{n}$ pour tout naturel $n$.
Déterminer $\lim↙{n→+∞}u_n$. - Soit $(v_n)$ la suite définie par $v_n={{5}/{n^2}+9}/{√{n}-1}$ pour tout naturel $n$ supérieur ou égal à 2.
Déterminer $\lim↙{n→+∞}v_n$. - Soit $(r_n)$ la suite définie par $r_n={3+0,4^n}/{2,1^n-6}$ pour tout naturel $n$.
Déterminer $\lim↙{n→+∞}r_n$.
Corrigé
Ce corrigé est très détaillé; les suivants le seront moins....
- $\lim↙{n→+∞}n^2=+∞$. Or 3>0. Donc $\lim↙{n→+∞}3n^2=+∞$ (limite d'un produit).
Par ailleurs $\lim↙{n→+∞}n=+∞$ et $\lim↙{n→+∞}-5=-5$.
Donc $\lim↙{n→+∞}3n^2+n-5=+∞$ (limite d'une somme).
Par ailleurs $\lim↙{n→+∞}√{n}=+∞$.
On rappelle alors que $u_n=(3n^2+n-5)√{n}$.
On obtient donc finalement $\lim↙{n→+∞}u_n=+∞$ (limite d'un produit). - $\lim↙{n→+∞}{1}/{n^2}=0$. Or ${5}/{n^2}=5{1}/{n^2}$. Donc $\lim↙{n→+∞}{5}/{n^2}=5×0=0$.
Par ailleurs $\lim↙{n→+∞}9=9$.
Donc $\lim↙{n→+∞}{5}/{n^2}+9=0+9=9$ (limite d'une somme).
Par ailleurs, comme $\lim↙{n→+∞}√{n}=+∞$ et $\lim↙{n→+∞}-1=-1$,
on obtient $\lim↙{n→+∞}√{n}-1=+∞$ (limite d'une somme).
On rappelle alors que $v_n={{5}/{n^2}+9}/{√{n}-1}$.
On obtient donc finalement $\lim↙{n→+∞}v_n=0$ (limite d'un quotient). - $-1$<$0,4$<$1$, donc $\lim↙{n→+∞}(0,4^n)=0$.
Or $\lim↙{n→+∞}3=3$. Donc $\lim↙{n→+∞}(3+0,4^n)=3$.
Par ailleurs, $2,1\text">"1$, donc $\lim↙{n→+∞}2,1^n=+∞$.
Et comme $\lim↙{n→+∞}-6=-6$, on obtient $\lim↙{n→+∞}2,1^n-6=+∞$.
On rappelle alors que $r_n={3+0,4^n}/{2,1^n-6}$.
On obtient donc finalement $\lim↙{n→+∞}r_n=0$ (limite d'un quotient).
Savoir faire
En cas de forme indéterminée dans une recherche de limite, il est souvent opportun de factoriser le terme dominant
(même si la factorisation est artificielle) (voir les exemples qui suivent).
 Exemples
Exemples
- Soit $(w_n)$ la suite définie par $w_n=5n^2-n+2$ pour tout naturel $n$.
Déterminer $\lim↙{n→+∞}w_n$. - Soit $(t_n)$ la suite définie par $t_n={-3n^2+n+4}/{2n+7}$ pour tout naturel $n$.
Déterminer $\lim↙{n→+∞}t_n$. - Soit $(p_n)$ la suite définie par $p_n=(n^2-n+1){1}/{n}$ pour tout naturel $n$ non nul.
Déterminer $\lim↙{n→+∞}p_n$.
Corrigé
- On obtient facilement $\lim↙{n→+∞}5n^2=+∞$ et $\lim↙{n→+∞}-n=-∞$, ce qui conduit à une forme indéterminée.
On factorise alors le terme "dominant" de la somme $w_n$.
$w_n=n^2(5-{1}/{n}+{2}/{n^2})$.
Or $\lim↙{n→+∞}n^2=+∞$ et $\lim↙{n→+∞}5-{1}/{n}+{2}/{n^2}=5-0+0=5$.
On obtient donc finalement $\lim↙{n→+∞}w_n=+∞$ (limite d'un produit). - On obtient "facilement" $\lim↙{n→+∞}-3n^2+n+4=-∞$ (il suffit de factoriser $n^2$) et $\lim↙{n→+∞}2n+7=+∞$, ce qui conduit à une forme indéterminée.
On factorise alors les termes "dominants" dans le quotient $t_n$ et on simplifie.
$t_n={n^2(-3+{1}/{n}+{4}/{n^2})}/{n(2+{7}/{n})}=n{-3+{1}/{n}+{4}/{n^2}}/{2+{7}/{n}}$.
Or $\lim↙{n→+∞}n=+∞$ et $\lim↙{n→+∞}{-3+{1}/{n}+{4}/{n^2}}/{2+{7}/{n}}={-3+0+0}/{2+0}={-3}/{2}=-1,5$.
Donc, comme $-1,5\text"<"0$, on obtient finalement $\lim↙{n→+∞}t_n=-∞$ (limite d'un produit). - On obtient "facilement" $\lim↙{n→+∞}n^2-n+1=+∞$ (il suffit de factoriser $n^2$) et $\lim↙{n→+∞}{1}/{n}=0$, ce qui conduit à une forme indéterminée.
Mais il suffit de simplifier après avoir factorisé!
$p_n=n^2(1-{1}/{n}+{1}/{n^2}){1}/{n}=n(1-{1}/{n}+{1}/{n^2})$
Or:$\lim↙{n→+∞}n=+∞$ et $\lim↙{n→+∞}1-{1}/{n}+{1}/{n^2}=1$
Donc finalement $\lim↙{n→+∞}p_n=+∞$ (limite d'un produit).
Autre méthode: on peut aussi développer!
On obtient: $p_n=n-1+{1}/{n}$.
Or $\lim↙{n→+∞}n=+∞$ et $\lim↙{n→+∞}-1+{1}/{n}=-1+0=-1$.
Donc finalement $\lim↙{n→+∞}p_n=+∞$ (limite d'une somme).
IV Raisonnement par récurrence
Axiome de récurrence
Soit $P_n$ une propriété dépendant du naturel $n$ et soit $n_0$ un naturel fixé.
Si l'on démontre que:
-
$P_{n_0}$ est vraie (c'est l'Initialisation)
-
Pour tout naturel $n≥n_0$,
si $P_n$ est vraie, alors $P_{n+1}$ est vraie (c'est l'Hérédité)
Alors, pour tout naturel $n≥n_0$, la propriété $P_n$ est vraie.
Exemple
Démontrer que:
pour tout réel $a$ strictement positif, pour tout naturel $n$, on a:
$(1+a)^n≥1+na$
Cette inégalité s'appelle l'inégalité de Bernoulli.
Corrigé
Soit $a$ un réel strictement positif.
Soit $P_n$ la propriété: $(1+a)^n≥1+na$.
Démontrons par récurrence que, pour tout naturel $n$, la propriété $P_n$ est vraie.
Initialisation:
On a: $(1+a)^0=1$, et: $1+0×a=1$. Et donc: $(1+a)^0≥1+0×a$.
Donc $P_{0}$ est vraie.
Hérédité:
Soit $n$ un entier naturel, supposons que $P_n$ soit vraie.
On a donc: $(1+a)^n≥1+na$
En multipliant chaque membre de l'inégalité par $1+a$ (qui est strictement positif), on obtient donc:
$(1+a)^n×(1+a)≥(1+na)×(1+a)$
Soit: $(1+a)^{n+1}≥1+a+na+na^2$
Soit: $(1+a)^{n+1}≥1+(n+1)a+na^2$
Et comme $na^2$ est clairement positif (ou nul), on obtient:
$(1+a)^{n+1}≥1+(n+1)a$
Donc $P_{n+1}$ est vraie.
Conclusion: pour tout naturel $n$, l'inégalité de Bernoulli est vraie.
 Exemple
Exemple
1. Démontrer que la fonction $f$, définie sur $[-1;+∞[$ par $f(x)=\√{x+1}$, est croissante.
2. Soit $u$ la suite définie par:
- $u_0=15$
- pour tout naturel $n$, $u_{n+1}=2\√{u_n+1}$
Démontrer que, pour tout naturel, $u_n$ existe et est positif.
3. Démontrer que $u$ est décroissante.
Solution...Corrigé
1. Pour tout $x$ dans $[-1;+∞[$, $x+1$ est positif (ce qui assure l'existence de $f(x)$ pour $x$ dans $[-1;+∞[$).
Dérivons la composée $f(x)=\√{x+1}$.
Ici: $f(x)=g(x+1)$ avec $g(z)=√{z}$.
Et donc: $(f(x))\,'=1×g\,'(x+1)$ avec $g'(z)={1}/{2√{z}}$.
Donc: $f'(x)=1×{1}/{2√{x+1}}={1}/{2√{x+1}}$.
Cette dérivée est positive.
$f$ est donc croissante.
2. Soit $P_n$ la propriété: "$u_n$ existe et est positif".
Démontrons par récurrence que, pour tout naturel $n$, la propriété $P_n$ est vraie.
Initialisation:
$u_0=15$. $u_0$ existe et $u_0≥0$. Donc $P_{0}$ est vraie.
Hérédité:
Soit $n$ un entier naturel, supposons que $P_n$ soit vraie.
$u_n$ existe.
De plus, $u_n≥0$. Donc: $u_n+1≥0+1$, soit: $u_n+1≥1$, et par là $u_n+1≥0$.
Et comme $u_{n+1}=2\√{u_n+1}$, on en déduit que $u_{n+1}$ existe et que $u_{n+1}≥0$.
Donc $P_{n+1}$ est vraie.
Conclusion: pour tout naturel $n$, $u_n$ existe et est positif.
3. Soit $Q_n$ la propriété: "$u_{n+1}≤u_n$".
Démontrons par récurrence que, pour tout naturel $n$, la propriété $Q_n$ est vraie.
Initialisation:
$u_0=15$. $u_1=2\√{u_0+1}=2\√{15+1}=2\√{16}=8$.
On a bien $u_{1}≤u_0$, et par là, $Q_{0}$ est vraie.
Hérédité:
Soit $n$ un entier naturel, supposons que $Q_n$ soit vraie.
On a donc: $u_{n+1}≤u_n$.
Or, les réels $u_{n+1}$ et $u_n$ sont dans $[0;+∞[$ (d'après le 2.), intervalle sur lequel $f$ est croissante (d'après le 1.).
Donc: $f(u_{n+1})≤f(u_n)$.
Soit: $\√{u_{n+1}+1}≤\√{u_{n}+1}$.
Donc: $2\√{u_{n+1}+1}≤2\√{u_{n}+1}$.
Donc: $u_{n+2}≤u_{n+1}$.
Ainsi, $P_{n+1}$ est vraie.
Conclusion: pour tout naturel $n$, $u_{n+1}≤u_n$.
Et par là, la suite $u$ est décroissante.
V Comparaisons
Théorème de comparaison
Si $\lim↙{n→+∞}u_n=+∞$ et si, à partir d'un certain rang, $v_n≥u_n$,
alors $\lim↙{n→+∞}v_n=+∞$.
Propriété
Si $\lim↙{n→+∞}u_n=l$ et si la suite $(u_n)$ est croissante,
alors, pour tout entier naturel $n$, $u_n≤l$.
Théorème des gendarmes
Si $\lim↙{n→+∞}u_n=l$ et si $\lim↙{n→+∞}w_n=l$ et
si, à partir d'un certain rang, $u_n≤v_n≤w_n$,
alors $\lim↙{n→+∞}v_n=l$.
Exemples
- Soit $(u_n)$ la suite définie par $u_n=2n^2+\sin n$ pour tout naturel $n$.
Déterminer $\lim↙{n→+∞}u_n$. - Soit $(w_n)$ une suite telle que $\lim↙{n→+∞}w_n=5$ et $w_8=6$.
Qu'en déduire? - Soit $(v_n)$ la suite définie par $v_n={(-1)^n}/{n^3+2}$ pour tout naturel $n$.
Déterminer $\lim↙{n→+∞}v_n$.
Corrigé
- Pour tout naturel $n$, $\sin n≥-1$.
Donc, pour tout naturel $n$: $2n^2+\sin n≥2n^2-1$, soit: $u_n≥2n^2-1$.
Or, comme $\lim↙{n→+∞}2n^2=+∞$ et $\lim↙{n→+∞}-1=-1$, on a: $\lim↙{n→+∞}2n^2-1=+∞$.
Par comparaison, on obtient: $\lim↙{n→+∞}u_n=+∞$. - $\lim↙{n→+∞}w_n=5$, donc, si la suite $(w_n)$ est croissante,
alors, pour tout entier naturel $n$, $w_n≤5$.
Or $w_8=6$, et par là $w_8\text">"5$.
Par conséquent, la suite $(w_n)$ n'est pas croissante.
Attention, cela ne signifie pas qu'elle est décroissante! - Pour tout naturel $n$, $-1≤(-1)^n≤1$, et donc: ${-1}/{n^3+2}≤v_n≤{1/{n^3+2}$.
Or, comme $\lim↙{n→+∞}n^3=+∞$ et $\lim↙{n→+∞}2=2$, on a: $\lim↙{n→+∞}n^3+2=+∞$,
et par là, comme $\lim↙{n→+∞}-1=-1$, on a: $\lim↙{n→+∞}{-1}/{n^3+2}=0$,
et comme $\lim↙{n→+∞}1=1$, on a: $\lim↙{n→+∞}{1}/{n^3+2}=0$.
Donc, d'après le "théorème des gendarmes", on obtient: $\lim↙{n→+∞}v_n=0$.
Définitions
La suite $(u_n)$ est majorée par M si et seulement si $∀ n ∈ \ℕ$, $u_n≤M$.
M est un majorant de la suite $(u_n)$.
La suite $(u_n)$ est minorée par $m$ si et seulement si $∀ n ∈ \ℕ$, $u_n≥m$.
$m$ est un minorant de la suite $(u_n)$.
La suite $(u_n)$ est bornée si et seulement si elle est majorée et minorée.
Théorèmes de convergence
Si $(u_n)$ est croissante et majorée, alors $(u_n)$ converge.
Si $(u_n)$ est décroissante et minorée, alors $(u_n)$ converge.
Théorèmes de divergence
Si $(u_n)$ est croissante et non majorée, alors $(u_n)$ diverge, et $\lim↙{n→+∞}u_n=+∞$.
Si $(u_n)$ est décroissante et non minorée, alors $(u_n)$ diverge, et $\lim↙{n→+∞}u_n=-∞$.
Propriété
Si $(u_n)$ est majorée par M et si $\lim↙{n→+∞}u_n=l$, alors $l≤M$.
Si $(u_n)$ est minorée par $m$ et si $\lim↙{n→+∞}u_n=l$, alors $l≥m$.
 Exemple
Exemple
Soit $u$ la suite définie par:
- $u_0=2$
- pour tout naturel $n$, $u_{n+1}={1}/{3}u_n+5$
- Montrer par récurrence que $u$ est majorée par 7,5.
- Démontrer que $u$ est convergente.
- Démontrer que $\lim↙{n→+∞}u_n=7,5$.
Corrigé
-
Soit $P_n$ la propriété: "$u_n≤7,5$".
Démontrons par récurrence que, pour tout naturel $n$, la propriété $P_n$ est vraie.
Initialisation: $u_0=2$. On a bien $u_0≤7,5$. Donc $P_{0}$ est vraie.
Hérédité:
Soit $n$ un entier naturel, supposons que $P_n$ soit vraie.
$u_n≤7,5$.
Donc: ${1}/{3}u_n+5≤{1}/{3}7,5+5$. Soit: $u_{n+1}≤7,5$.
Donc $P_{n+1}$ est vraie.
Conclusion: pour tout naturel $n$, $u_n≤7,5$. -
$u$ étant majorée, il suffit de montrer qu'elle est croissante pour prouver qu'elle converge.
On notera que cette condition est suffisante, mais qu'elle n'est pas nécessaire!
Soit $n$ un entier naturel.
$u_{n+1}≥u_n⇔{1}/{3}u_n+5≥u_n⇔u_n({1}/{3}-1)≥-5⇔u_n≤(-5){3}/{-2}⇔u_n≤7,5$.
La dernière inégalité étant vraie pour tout naturel $n$, la première l'est également, et par là, $u$ est croissante.
Comme $u$ est croissante et majorée, elle converge. -
Soit $l$ sa limite.
On rappelle que $\lim↙{n→+∞}u_{n+1}=\lim↙{n→+∞}u_n$.
Donc, par passage à la limite dans l'égalité $u_{n+1}={1}/{3}u_n+5$,
on en déduit que $l={1}/{3}l+5$. Soit: $l×(1-{1}/{3})=5$. Et donc: $l=7,5$.
Donc $u$ admet pour limite 7,5.