Succession d'épreuves indépendantes, schéma de Bernoulli
A SAVOIR: le cours sur Succession d'épreuves indépendantes, schéma de Bernoulli
Exercice 1
Un examen comporte 3 épreuves, A, B et C.
Un candidat quelconque passe cet examen.
A: "le candidat a réussi l'épreuve A"
B: "le candidat a réussi l'épreuve B"
C: "le candidat a réussi l'épreuve C"
On a déterminé statistiquement que: $p(A)=0,7$ et $p(B)=0,2$, mais on ne connait pas $p(C)$
Le candidat est reçu à cet examen s'il a réussi au moins deux épreuves sur trois.
Soit S: "le candidat a réussi l'examen"
On sait que: $p(S)=0,388$.
Déterminer $p(C)$
Solution...
Corrigé
Nous sommes en présence de 3 épreuves indépendantes.
En posant $p(C)=p$, nous pouvons dresser l'arbre de probabilité suivant.
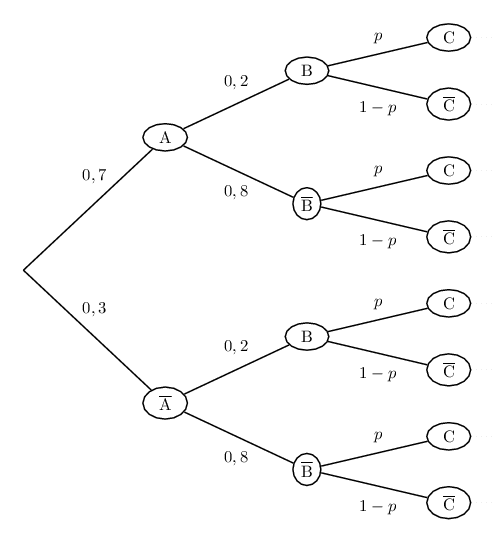
On a: $S=\{(A,B,C),(A,B,\ov{C}),(A,\ov{B},C),(\ov{A},B,C)\}$
On obtient alors:
$p(S)=p((A,B,C))+p((A,B,\ov{C}))+p((A,\ov{B},C))+p((\ov{A},B,C))$
$0,388=0,7×0,2×p + 0,7×0,2×(1-p)+0,7×0,8×p+0,3×0,2×p$
Soit: $0,388=0,14p+0,14-0,14p+0,56p+0,06p$
Soit: $0,248=0,62p$
Et par là: $p=0,4$