Succession d'épreuves indépendantes, schéma de Bernoulli
A SAVOIR: le cours sur Succession d'épreuves indépendantes, schéma de Bernoulli
Exercice 5
Le plan est rapporté à un repère orthonormé d'origine O.
Un robot est situé en O et il va rejoindre le point M(7;9) en $n$ étapes.
A chaque étape, soit il effectue une translation de vecteur ${i}↖{→}$( 1 ; 0 ), soit il effectue une translation de vecteur ${j}↖{→}$( 0 ; 1 ).
On notera, si besoin:
i: " le robot effectue une translation de vecteur ${i}↖{→}$ "
j: " le robot effectue une translation de vecteur ${j}↖{→}$ "
- Combien vaut $n$?
- Combien de chemins différents permettent au robot d'atteindre le point M?
-
Le robot effectue 16 étapes.
A chaque fois, les événements i et j sont équiprobables.
Quelle est la probabilité que le robot arrive en M? (arrondie à 0,01)
- Cette fois-ci, le robot effectue toujours 16 étapes, mais, à chaque fois, ses choix ne sont pas équiprobables. On a: $p(i)=0,4$, et par là, $p(j)=0,6$.
Quelle est la probabilité que le robot arrive en M? (arrondie à 0,01)
Solution...
Corrigé
-
Le robot va rejoindre le point M(7;9) en $n$ étapes.
Pour atteindre le point M, le robot doit effectuer 7 translations de vecteur ${i}↖{→}$( 1 ; 0 )et 9 translations de vecteur ${j}↖{→}$( 0 ; 1 ).
Or $7+9=16$. Donc $n=16$. -
Un chemin possible correspond à une combinaison de 7 éléments pris parmi 16, qui sont les rangs des 7 translations.
Par exemple, { 1, 2, 4, 5, 9, 12, 13} code le chemin suivant (i, i, j, i, i, j, j, j, i, j, j, i, i, j, j, j).
Or $(\table 16; 7)=11\,440$.
Donc il y a $11\,440$ chemins possibles! - Le nombre de chemins possibles est $2^{16}=65\,635$. Ils sont équiprobables. Or $11\,440$ de ces chemins conduisent à M. Donc la probabilité cherchée vaut ${11\,440}/{65\,635}≈0,17$
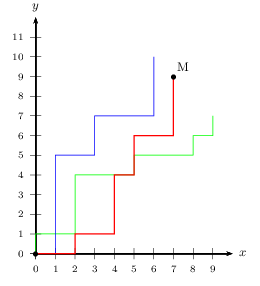
Sur le schéma ci-dessus, seul le chemin en rouge est favorable. - Cette fois-ci, les chemins ne sont pas équiprobables. Nous devons raisonner autrement.
Chacune des étapes constitue une épreuve de Bernoulli de paramètre $p=0,4$ et dont le succès est i.
Les 16 étapes sont indépendantes.
Soit X la variable aléatoire dénombrant les succès.
Par conséquent X est une binomiale de paramètres 16 et 0,4.
Soit: $X=B (\,16\,;\,0,4\,)$
La probabilité cherchée est $p(X=7)=(\table 16; 7)\,0,4^7(1-0,4)^{16-7}=11\,440×0,4^7×0,6^9≈0,19$.
A la calculatrice, on peut obtenir directement: $p(X=7)≈0,19$.