Succession d'épreuves indépendantes, schéma de Bernoulli
A SAVOIR: le cours sur Succession d'épreuves indépendantes, schéma de Bernoulli
Exercice 6
Le directeur d'un hôtel tente de louer toutes ses chambres malgré les défections de quelques clients.
Il a instauré un système de réservations et a constaté que $20\%$ des clients réservent par téléphone, les autres utilisent internet.
Mais certains clients ayant réservé ne viennent pas; cela concerne
$4\%$ des clients ayant réservé par téléphone, et $10\%$ des clients ayant réservé par internet.
On considère une réservation prise au hasard.
Soit T : " la réservation a été faite par téléphone ";
I : " la réservation a été faite par Internet " ;
P : " le client se présente à l'hôtel ".
-
Représenter la situation par un arbre de probabilité.
Montrer que $p(P)=0,912$ - On considère un client présent dans l'hôtel.
Quelle est la probabilité qu'il ait réservé par internet? (arrondie au millième) - Le directeur sait qu'il ne peut accueillir que 100 clients. Mais il a accordé 106 réservations.
Soit X la variable aléatoire qui dénombre les clients qui se présentent à l'hôtel.
Justifier que la variable aléatoire X suit une loi binomiale dont on donnera les paramètres. - Quelle est la probabilité que les 106 clients de présentent à l'hôtel? (arrondie à $10^{-5}$)
- Quelle est la probabilité, arrondie au centième) que le directeur se retrouve en situation de surréservation (c'est à dire qu'au moins 101 clients se présentent à l'hôtel)?
- Quel est le nombre maximum de réservations que doit accorder le directeur pour être certain à $99\%$ que tous les clients qui se présenteront à l'hôtel aient une chambre?
Solution...
Corrigé
-
Voici un arbre de probabilité convenable.
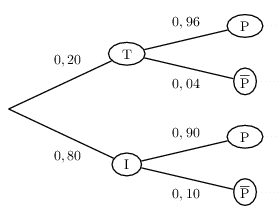
$\{T;I\}$ constitue une partition de l'univers.
On sait que $p(P)=p(T∩P)+p(I∩P)$ (par application de la formule des probabilités totales).
Soit: $p(P)=p(T)×p_T(P)+p(I)×p_I(P)$
Soit: $p(P)=0,20×0,96+0,80×0,90$
Et donc: $p(P)=0,912$ - On cherche: $p_P(I)={p(I∩P)}/{p(P)}={0,80×0,90}/{0,912}≈$$0,789$
- Le directeur sait qu'il ne peut accueillir que 100 clients. Mais il a accordé 106 réservations.
Soit X la variable aléatoire qui dénombre les clients qui se présentent à l'hôtel.
L'expérience consiste à répéter 106 fois de manière indépendante une expérience à 2 issues: $P$ et $\ov P$, et on a $p(P)=0,912$.
On en déduit que X suit une loi binomiale de paramètres $n=106$ et $p=0,912$. - On cherche: $p(X=106)=0,912^{106}≈$$6×10^{-5}$
- On cherche: $p(X≥101)=p(101≤X≤106)=p(X≤106)-p(X≤100)≈1-0,91≈$$0,09$
- On cherche le plus grand entier $n$ tel que $p(Y≤100)≥0,99$, où Y est la binomiale de paramètres $n$ inconnu et $p=0,912$.
Par essais successifs, on obtient:
pour $n=104$, $p(Y≤100)≈0,984$
pour $n=103$, $p(Y≤100)≈0,995$.
Donc le directeur doit accorder au plus 103 réservations pour être certain à $99\%$ que tous les clients qui se présenteront à l'hôtel auront une chambre.