Dérivation
A SAVOIR: le cours sur la dérivation
Exercice 5
La tangente $t$ à $\C_f$ en $-0,5$ traverse $\C_f$.
Déterminer graphiquement la convexité de la fonction $f$ définie sur $[-2\,;\,0,6\,]$.
En déduire le sens de variation de $f\,'$ et le signe de $f"$ sur $[-2\,;\,0,6\,]$.
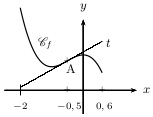
Corrigé
Il est évident que $f$ est convexe sur $[-2\,;-0,5]$ (car $\C_f$ y est au dessus de ses tangentes),
et concave sur $[-0,5\,;\,0,6]$ (car $\C_f$ y est en dessous de ses tangentes).
Par conséquent, $f'$ est croissante sur $[-2\,;-0,5]$, et $f"$ y est positive .
Et $f'$ est décroissante sur $[-0,5\,;\,0,6]$, et $f"$ y est négative.