 Oral second groupe
Oral second groupe
L'épreuve consiste en une interrogation du candidat, visant à apprécier sa maîtrise des connaissances de base.
Montrez donc que vous savez votre cours. Si vous séchez, n'hésitez pas à proposer des pistes de réflexion;
l'interrogateur vous guidera. Temps de préparation: 20 minutes.
Durée de l'interrogation: 20 minutes.
SUJET 2
Exercice 1
L'espace est muni d'un repère orthonormal.
Soit le point A de coordonnées (1 ; -1 ; 2).
Soit le plan P d'équation cartésienne $3x-y+2=0$.
Déterminer une équation paramétrique de la droite $d$ orthogonale à P et passant par A.
Cette droite passe-t-elle par B(7 ; -3 ; 2)?
Exercice 2
Soit $f$ définie sur $[1;+∞[$ par $f(x)=x^2e^{2x+1}$.
Déterminer le sens de variation de $f$ sur $[1;+∞[$.
Dresser le tableau de variation de $f$ sur $[1;+∞[$.
facultatif: Montrer que l'équation $f(x)=22$ admet une solution unique sur $[1;+∞[$.
Corrigé
Exercice 1
A savoir!Déterminer un vecteur normal à un plan donné par une équation cartésienne.
Déterminer une équation paramétrique d'une drtoite définie par un point et un vecteur directeur.
Vérifier si une droite passe par un point donné.
P, d'équation cartésienne $3x-y+2=0$, admet pour vecteur normal ${n}↖{→}(\,3\,;\,-1\,;\,0\,)$.
Comme $d$ est orthogonale à P, elle admet ${n}↖{→}$ pour vecteur directeur.
Et comme $d$ passe par A(1 ; -1 ; 2), elle a pour équation paramétrique: $\{\table x=1+3×t;y=-1+(-1)×t; z=2+0×t$
Soit: $\{\table x=1+3t;y=-1-t; z=2$
$d$ passe par B(7 ; -3 ; 2) si et seulement si il existe un réel $t$ tel que $\{\table 7=1+3t;-3=-1-t; 2=2$ (1)
(1) $ ⇔$ $\{\table 2=t;t=2; 2=2$
(1) admet une solution ($t=2$), et par là, $d$ passe par B.
Exercice 2
A savoir!Les dérivées de $uv$ et de $e^u$.
Déterminer le signe d'un produit, de $ax+b$.
Une exponentielle est strictement positive.
Construire un tableau de variation sans inverser $f$ et $f'$.
Déterminer la limite de $e^{u(x)}$.
On pose $f=uv$ avec $u=x^2$ et $v=e^{2x+1}$.
D'où $f\,'=u'v+uv'$ avec $u'=2x$ et $v'=2e^{2x+1}$.
Donc $f\,'(x)=2x×e^{2x+1}+x^2×2e^{2x+1}=e^{2x+1}(2x+2x^2)=2x(1+x)e^{2x+1}$.
$f\,'$ est un produit de 3 facteurs.
$2x$ s'annule en 0 et est strictement positif pour $x\text">"0$.
$1+x$ s'annule en -1 et est strictement positif pour $x\text">"-1$.
$e^{2x+1}$ reste strictement positif pour tout $x$.
Donc, sur $[1;+∞[$, $f\,'$ est strictement positive, et par là, $f$ y est strictement croissante.
Par ailleurs: $f(1)=e^3$.
Reste à trouver $\lim↙{x→+∞}f(x)$.
On a: $\lim↙{x→+∞}2x+1=+∞$. Or $\lim↙{y→+∞}e^y=+∞$. Donc $\lim↙{x→+∞}e^{2x+1}=+∞$.
Par ailleurs $\lim↙{x→+∞}x^2=+∞$.
Donc finalement: $\lim↙{x→+∞}f(x)=+∞$.
D'où le tableau de variation de $f$.
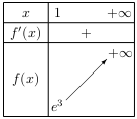
D'après le tableau de variation ci-dessus, la fonction $f$ est continue et strictement croissante sur $[1;+∞[$.
Or, d'une part: 22 est strictement supérieur à $f(1)=e^3≈20$,
et d'autre part: $\lim↙{x→+∞}f(x)=+∞$.,
Donc, d'après le théorème de la bijection, l'équation $f(x)=22$ admet une unique solution sur $[1;+∞[$.