 Oral second groupe
Oral second groupe
L'épreuve consiste en une interrogation du candidat, visant à apprécier sa maîtrise des connaissances de base.
Montrez donc que vous savez votre cours. Si vous séchez, n'hésitez pas à proposer des pistes de réflexion;
l'interrogateur vous guidera. Temps de préparation: 20 minutes.
Durée de l'interrogation: 20 minutes.
SUJET 3
Exercice 1
Lors d'un tournoi qualificatif, un joueur fait trois parties d'échecs contre trois adversaires différents: A, B et C.
On définit les événements suivants.
A: "le joueur a gagné contre l'adversaire A"
B: "le joueur a gagné contre l'adversaire B"
C: "le joueur a gagné contre l'adversaire C"
Compte tenu des classements des joueurs, on a déterminé statistiquement que: $p(A)=0,7$ et $p(B)=0,2$, mais on ne connait pas $p(C)$
Le joueur est qualifié s'il a gagné au moins deux parties sur trois.
Soit S: "le joueur est qualifié"
On sait que: $p(S)=0,388$.
Déterminer $p(C)$.
Exercice 2
Déterminer la dérivée de la fonction, puis le signe de sa dérivée,
puis le sens de variation de la fonction sur l'intervalle I pour:
$n(x)=2√{x^2+1}+(3x+1)^2$ avec $I=]0;2]$.
On admet que $n'(0)=6$. Déterminer une équation de la tangente $d$ à $\C_n$ en 0.
Corrigé
Exercice 1
A savoir!Construire un arbre de probabilités.
Déterminer la probabilité d'un événement situé sur une "feuille".
Nous sommes en présence de 3 épreuves indépendantes.
En posant $p(C)=p$, nous pouvons dresser l'arbre de probabilité suivant.
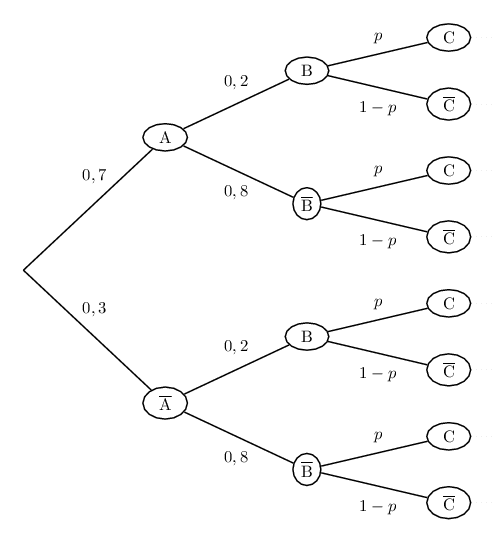
On a: $S=\{(A,B,C),(A,B,\ov{C}),(A,\ov{B},C),(\ov{A},B,C)\}$
On obtient alors:
$p(S)=p((A,B,C))+p((A,B,\ov{C}))+p((A,\ov{B},C))+p((\ov{A},B,C))$
$0,388=0,7×0,2×p + 0,7×0,2×(1-p)+0,7×0,8×p+0,3×0,2×p$
Soit: $0,388=0,14p+0,14-0,14p+0,56p+0,06p$
Soit: $0,248=0,62p$
Et par là: $p=0,4$
Exercice 2
A savoir!Les dérivées de $uv$ et de $√{u}$.
Déterminer le signe d'une expression.
Relier le signe de la dérivée $n'$ au sens de variation de la fonction $n$.
L'équation de la tangente à $\C_n$ en $a$: $y=n(a)+n'(a)×(x-a)$.
Dérivons $n(x)=2√{x^2+1}+(3x+1)^2$
On pose $u=x^2+1$. Donc $u\,'=2x$.
De même $w=3x+1$. Donc $w\,'=3$.
Ici $n=2√{u}+w^2$ et donc $n\,'=2{u\,'}/{2√{u}}+2w\,'w$.
Donc $n\,'(x)=2 ×{2x}/{2√{x^2+1}}+2 ×3 ×(3x+1)={2x}/{√{x^2+1}}+18x+6$.
Malheureusement, $n\,'(x)$ est une somme. Or le signe d'une somme n'est évident que si tous les termes sont de même signe. Mais nous allons montrer qu'ici, c'est le cas!
$√{x^2+1}$ est strictement positif pour tout $x$.
Or, sur $I$: $2x$>$0$.
Donc, sur $I$, le quotient ${2x}/{√{x^2+1}}$ est strictement positif.
Par ailleurs, sur $I$: $18x+6$>$0$.
Donc les deux termes constituant $n\,'(x)$ sont strictement positifs sur $I$.
Et finalement, sur $I$, $n\,'(x)$>$0$.
Donc $n$ est strictement croissante sur I.
On calcule: $n(0)==2√{0^2+1}+(3×0+1)^2=3$. Or $n'(0)=6$.
Donc la tangente $d$ a pour équation: $y=3+6×(x-0)$; soit: $y=6x+3$