 Oral second groupe
Oral second groupe
L'épreuve consiste en une interrogation du candidat, visant à apprécier sa maîtrise des connaissances de base.
Montrez donc que vous savez votre cours. Temps de préparation: 20 minutes.
Durée de l'interrogation: 20 minutes.
SUJET 5
Exercice 1
On considère l'arbre de probabilités suivant:
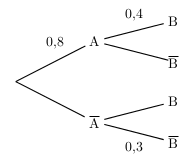
- Recopier et compléter cet arbre.
- Que représente la valeur 0,8?
Que représente la valeur 0,4? - Déterminer $p(A∩B)$.
- Déterminer $p(B)$.
- facultatif: Déterminer $p(A∪B)$.
- facultatif: Déterminer $p_B(A)$.
Exercice 2
$f(x)=2e^{3x}$. Déterminer une équation de la tangente $t$ à $\C_f$ en 1.
facultatif: Montrer que cette tangente est parallèle à la droite $d$ d'équation $y=6e^3x+7$.
Solution...
Corrigé
Exercice 1
A savoir!Construire un arbre de probabilités; ne pas confondre $p_A(B)$ et $p(A∩B)$.
Connaître les formules $p(A∩B)=p(A)×p_A(B)$ et $p_B(A)={p(A∩B)}/{p(B)}$.
Connaître la formule des probabilités totales.
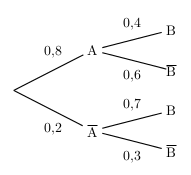
- On a: $p(A)=0,8$ (c'est une probabilité "simple")
et $p_A(B)=0,4$ (c'est une probabilité conditionnelle). - $p(A∩B)=p(A)×p_A(B)=0,8×0,4=0,32$.
- Par application de la formule des probabilités totales, on obtient:
$p(B)=p(A∩B)+p(A↖{-}∩B)=0,32+p(A↖{-})×p_{A↖{-}}(B)=0,32+0,2×0,7=0,32+0,14=0,46$. - $p(A∪B)=p(A)+p(B)-p(A∩B)=0,8+0,46-0,32=0,94$
- $p_B(A)={p(A∩B)}/{p(B)}={0,32}/{0,46}≈0,70$
Exercice 2
A savoir!La dérivée de $ku$ et celle de $e^u$.
L'équation de la tangente à $\C_f$ en $a$: $y=f(a)+f'(a)×(x-a)$.
On pose $f=2e^u$ avec $u=3x$.
Donc $f\,'=2u'e^u$ avec $u'=3$.
Donc $f\,'(x)=2×3e^{3x}=6e^{3x}$.
En particulier: $f\,'(1)=6e^{3×1}=6e^3$.
Par ailleurs: $f\,(1)=2e^{3×1}=2e^3$.
Donc $t$ admet pour équation: $y=2e^3+6e^3(x-1)$.
Soit: $y=2e^3+6e^3x-6e^3=6e^3x-4e^3$.
Finalement, $t$ a pour équation $y=6e^3x-4e^3$.
$d$ et $t$ ont toutes les deux le même coefficient directeur $6e^3$; elles sont donc parallèles.