 Représentations paramétriques et équations cartésiennes
Représentations paramétriques et équations cartésiennes
Exercice 2
Un décorateur veut tendre une toile plane dans un édifice en forme de tétraèdre.
Pour des raisons esthéthiques, il veut absolument que cette toile affleure 3 points P, Q et R qu'il a placés sur certaines faces de l'édifice.
Le tétraèdre ABCD est dessiné ci-après.
Figure 1
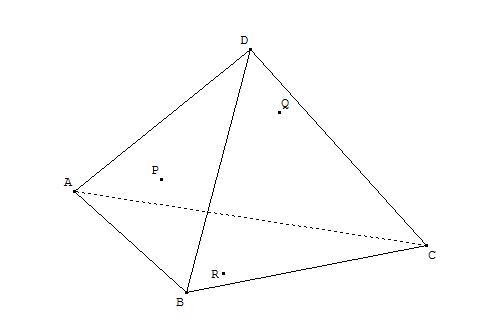
Le point P est sur la face ABD.
Le point Q est sur la face BCD.
Le point R est sur la face ABC.
La section du tétraèdre ABCD par le plan (PQR) est le quadrilatère XYZT.
Le décorateur recherche les positions exactes des points X, Y, Z et T.
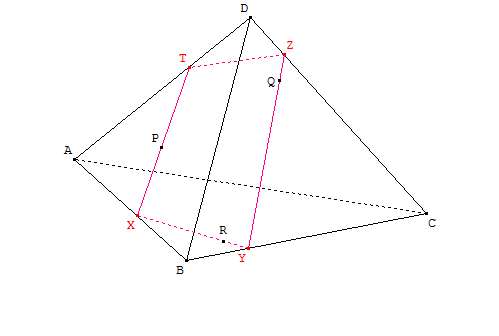
Dans tout ce qui suit, les points A, B, C, D, P, Q, R, X, Y et Z sont supposés distincts deux à deux.
Partie A
Nous allons déterminer la section XYZT par des constructions géométriques.
Reproduire la figure 1 (sans la section), et compléter la au fur et à mesure.
Soit M le point d'intersection de la droite (DP) avec la droite (AB).
Soit N le point d'intersection de la droite (DQ) avec la droite (BC).
- Pourquoi les droites (MN) et (PQ) sont-elles coplanaires?
-
Soit K le point d'intersection des droites (MN) et (PQ).
On admet que les plans (PQR) et (ABC) sont sécants.
Donner 2 points appartenant à l'intersection du plan (PQR) et du plan (ABC). - Déterminer graphiquement les points X et Y, puis terminer la section.
Partie B
Nous allons retrouver la section XYZT par des constructions analytiques.
On se place dans un repère du plan (orthonormal si cela vous fait plaisir) tel que les points A, B, C et D aient les coordonnées suivantes.
A( 0 ; -2 ; 0 ) B( 2 ; 0 ; 0 ) C( 0 ; 2 ; 0 ) D( 0 ; 0 ; 2 ).
Par ailleurs, les points P, Q et R ont les coordonnées suivantes.
P( 0,6 ; -0,8 ; 0,6 ) Q( 0,2 ; 0,4 ; 1,4 ) R( 1,4 ; 0,2 ; 0 )
- Déterminer les coordonnées des vecteurs ${PQ}↖{→}$ et ${PR}↖{→}$.
Montrer que, tout point $M(x;y;z)$ appartient au plan (PQR) si et seulement si il existe deux réels $t$ et $t'$ tels que $\{\table x=0.6-0.4t+0.8t'; y=-0.8+1.2t+t'; z=0.6+0.8t-0.6t'$
On dit alors que le plan (PQR) admet pour représentation paramétrique $\{\table x=0.6-0.4t+0.8t'; y=-0.8+1.2t+t'; z=0.6+0.8t-0.6t'$
- On admet que le plan (ABC) admet pour représentation paramétrique $\{\table x=2a; y=-2+2a+4b; z=0$
Vérifier que R est bien dans le plan (ABC). - Soit $d$ la droite admettant pour représentation paramétrique $\{\table x=1.4+{2}/{3}t; y=0.2+{7.6}/{3}t; z=0$
On admet que les plans (PQR) et (ABC) sont sécants.
Montrer que les plans (PQR) et (ABC) se coupent selon la droite $d$. - Déterminer les coordonnées $(e;f;g)$ du point X, intersection de la droite $d$ avec la droite (AB).
Ces coordonnées seront arrondies à 0,01 près.
On pourrait de même déterminer les coordonnées des points Y, Z et T.
Corrigé
Partie A
-
M est le point d'intersection de la droite (DP) avec la droite (AB), donc il est sur (DP), et donc dans le plan (DPQ).
N est le point d'intersection de la droite (DQ) avec la droite (BC), donc il est sur (DQ), et donc dans le plan (DPQ).
M et N étant dans le plan (DPQ), la droite (MN) est donc dans le plan (DPQ).
Or la droite (PQ) est évidemment dans le plan (DPQ).
Donc les droites (MN) et (PQ) sont toutes deux dans le plan (DPQ); elles sont donc coplanaires.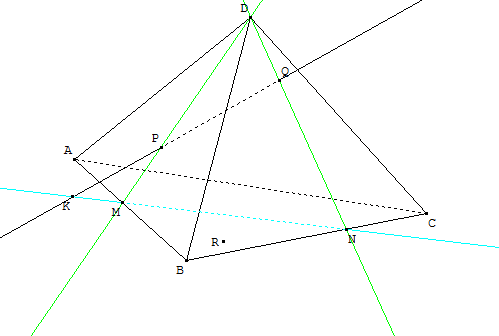
- Comme M est sur la droite (AB), il est donc dans le plan (ABC). De même, il est clair que N est également dans (ABC). Donc la droite (MN) est incluse dans (ABC).
Et comme K est sur (MN), K est donc dans le plan (ABC).
Par ailleurs, comme K est dans (PQ), il est dans le plan (PQR).
Donc finalement K appartient à l'intersection des plans (ABC) et (PQR).
Par ailleurs, R est, par hypothèse, dans le plan (ABC), et il est également évidemment dans le plan (PQR).
Donc R appartient à l'intersection des plans (ABC) et (PQR).
L'intersection des plans (ABC) et (PQR) contient donc les points K et R. - Comme les plans (PQR) et (ABC) sont sécants, d'après ce qui précède, ils se coupent selon la droite (KR).
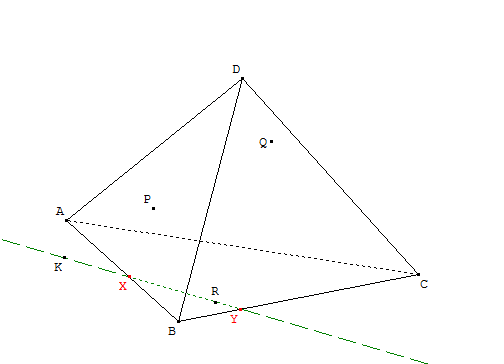
Le point X est alors à l'intersection de (KR) et de (AB).
Le point Y est alors à l'intersection de (KR) et de (BC).
La section s'obtient en traçant [XY], puis en traçant [XT], où T est à l'intersection de (XP) et de (AD), puis en traçant [YZ], où Z est à l'intersection de (YQ) et de (DC).
Elle se termine en traçant [TZ].

Partie B
- On obtient facilement: ${PQ}↖{→}$( -0.4 ; 1.2 ; 0.8 ) et ${PR}↖{→}$( 0.8 ; 1 ; -0.6 )
Ces deux vecteurs, non colinéaires (ils sont non nuls et leurs coordonnées ne sont pas proportionnelles), forment une base du plan vectoriel (PQR).
Comme P appartient à (PQR), M est sur (PQR) si et seulement si il existe deux réels $t$ et $t'$ tels que ${PM}↖{→}=t.{PQ}↖{→}+t'.{PR}↖{→}$
Soit: $\{\table x-0,6=-0.4t+0.8t'; y+0.8=1.2t+t'; z-0.6=0.8t-0.6t'$
Soit: $\{\table x=0.6-0.4t+0.8t'; y=-0.8+1.2t+t'; z=0.6+0.8t-0.6t'$
Donc le plan (PQR) a bien pour représentation paramétrique $\{\table x=0.6-0.4t+0.8t'; y=-0.8+1.2t+t'; z=0.6+0.8t-0.6t'$
- Le plan (ABC) admet pour représentation paramétrique $\{\table x=2a; y=-2+2a+4b; z=0$
Or on a: R( 1,4 ; 0,2 ; 0 ). On résout donc: $\{\table 1.4=2a; 0.2=-2+2a+4b; 0=0$
$\{\table 0.7=a; 0.2=-2+2×0.7+4b$
$\{\table a=0.7; b=0.2$
Le système admet un couple solution, ce qui prouve que R est bien dans le plan (ABC). - Le plan (ABC) admet pour représentation paramétrique $\{\table x=2a; y=-2+2a+4b; z=0$
Or le plan (PQR) a pour représentation paramétrique $\{\table x=0.6-0.4t+0.8t'; y=-0.8+1.2t+t'; z=0.6+0.8t-0.6t'$
On résout donc: $\{\table x=2a=0.6-0.4t+0.8t'; y=-2+2a+4b=-0.8+1.2t+t'; z=0=0.6+0.8t-0.6t'$
La dernière ligne donne immédiatement: $t'=1+{4}/{3}t$.
La première ligne donne alors: $x=2a=0.6-0.4t+0.8(1+{4}/{3}t)=1.4+{2}/{3}t$
Et enfin, la seconde ligne donne: $y=-2+2a+4b=-0.8+1.2t+1+{4}/{3}t=0.2+{7.6}/{3}t$
Et par là, les plans (PQR) et (ABC) se coupent selon la droite d'équation paramétrique: $\{\table x=1.4+{2}/{3}t; y=0.2+{7.6}/{3}t; z=0$
Il s'agit bien de la droite $d$.
- On obtient: ${AB}↖{→}(2;2;0)$. Et comme on a: A( 0 ; -2 ; 0 ), la droite (AB) a pour représentation paramétrique $\{\table x=2a; y=-2+2a; z=0$
On résout donc: $\{\table x=2a=1.4+{2}/{3}t; y=-2+2a=0.2+{7.6}/{3}t; z=0=0$
La première ligne et la seconde donnent: $-2+1,4+{2}/{3}t=0,2+{7,6}/{3}t$
Et par là: $t=-{2,4}/{5,6}$
Et donc finalement: $\{\table x=1.4+{2}/{3}×(-{2.4}/{5.6})≈1.11; y=0.2+{7.6}/{3}×(-{2.4}/{5.6})≈-0.89; z=0=0$
Donc: $e≈1,11$, $f≈-0,89$ et $g=0$.
On pourrait de même déterminer les coordonnées des points Y, Z et T.