 Fonction logarithme népérien
Fonction logarithme népérien
A SAVOIR: le cours sur la fonction ln
Exercice 6
Partie A algorithme de prosthaphérèse
A la Renaissance, le développement de certaines activités humaines comme l’astronomie, le commerce et la navigation nécessite la possibilité d'effectuer rapidement des calculs compliqués.
Déjà connue des astronomes arabes au X ème siècle, la prosthaphérèse (du grec "prosthesis" ajouter et "aphaeresis" soustraire) est redécouverte;
c'est une méthode permettant d'obtenir des produits ou des quotients en n'utilisant que des additions ou des soustractions grâce à des tables trigonométriques.
Ce système fera concurrence aux logarithmes de Neper bien après la parution de ses propres tables.
Voyons comment l'algorithme de prosthaphérèse fonctionne.
Pour l'utiliser, il convient de posséder une table trigonométrique, et de connaître le type de formule suivant:
$\sin a .\sin b={1}/{2}(\cos(a-b)-\cos(a+b))$
Premier calcul
Tentons de multiplier $A=20,6546$ par $B=518,922$ à l'aide de cette méthode.
On pose $p=A ×B$
Il convient de ramener ce calcul à un produit de nombres $a$ et $b$ situés entre 0 et 1 pour pouvoir utiliser l'extrait de table de sinus et de cosinus (dite "table trigonométrique") ci-dessous.

Les angles sont donnés en degrés décimaux ().
Ce n'était pas le cas à l'époque, l'écriture décimale n'étant pas encore inventée. Les angles étaient mesurés en degrés, minutes et secondes.
En outre, un sinus n'était pas considéré comme un nombre (sans unité), mais comme la longueur de la demi-corde de l'arc double d'un cercle de rayon fixé (souvent très grand).
Par exemple, pour un rayon de $1\,000$, le sinus de l'époque valait $1\,000$ fois le sinus actuel.
La table proposée ci-dessus est une table moderne par soucis de simplification...
On rappelle que $p=A ×B$ avec $A=20,6546$ par $B=518,922$
On pose: $p=10^{n}×a×b$ où $a$ et $b$ sont inférieurs à 1 et les plus grands possible.
On prend alors: $a=0,206546$ et $b=0,518922$.
- Que vaut $n$?
-
On pose alors: $a=\sin α$ et $b=\sin β$
Déterminer $α$ et $β$ à l'aide de la table.
Si les sinus n'avaient pas été dans la table, il aurait fallu approximer les valeurs des angles. - Calculer $α-β$ et $α+β$ (au XVI ème siècle, cela se faisait sans calculatrice!).
-
Déterminer $\cos(α-β)$ et $\cos(α+β)$ à l'aide de la table.
On rappelle si nécessaire que, pour tout $x$, $\cos (x)=\cos(-x)$. - Calculer ${1}/{2}(\cos (α-β)-\cos (α+β))$ (sans calculatrice!).
-
En déduire la valeur $a×b$, puis finalement celle du produit $p$.
Comparer avec le produit obtenu avec votre calculatrice.
Second calcul
Voici un autre extrait de table de sinus et de cosinus

 Multiplier $A=7490,71$ par $B=26,2358$ en s'inspirant de l'exemple précédent.
Multiplier $A=7490,71$ par $B=26,2358$ en s'inspirant de l'exemple précédent.
Partie B algorithme de Neper
Certaines opérations de l'algorithme de prosthaphérèse sont chronophages; il s'agit des 3 additions ou soustractions et de la division par 2 (à faire sans calculatrice!).
D'autres méthodes existent, par exemple en utilisant des tables d'intérêts.
Mais, toutes les méthodes existantes à l'époque sont relativement longues, et elles ne donnent des résultats précis que pour les nombres
qui sont dans les tables. Pour les autres, elles ne fournissent qu'un encadrement parfois grossier du résultat.
Neper va inventer un procédé plus efficace, qui sera amélioré par l'anglais Briggs (1556-1630)
Ce dernier a proposé une méthode basée sur une table de "logarithmes décimaux".
Voyons ceci sur un exemple.
On définit la fonction logarithme décimal, notée log, par $\log (x)={\ln x}/{\ln 10}$ pour tout $x$ strictement positif.
a. Montrer que cette fonction vérifie: $\log a +\log b=\log ab$ pour tous $a$ et $b$ strictement positifs.
b. Montrer que $\log 1=0$, que $\log 10 =1$ et que $\log 10^n =n$ pour tout entier $n$
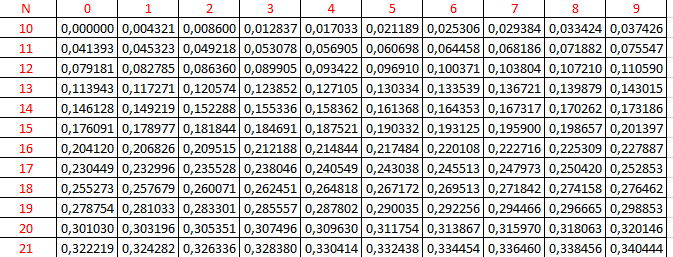
Voici un extrait d'une table de la fonction logarithme décimal.
Ici, le chiffre des unités et celui des dixièmes du nombre N figurent dans la colonne de gauche et le chiffre des centièmes dans la première ligne.
À l'intersection d'une ligne et d'une colonne, on lit la valeur de $\log(N)$.
Les tables de Neper étaient différentes de celle qui est proposée, mais elles possédaient le même type de propriétés (voir exercice 9 )
Tentons de multiplier $A=1,32$ par $B=15,6$ à l'aide de cette table.
Etape 1.
On se place sur la ligne 13 et dans la colonne 2 et on lit 0,120574. On peut donc conclure que
$\log A=\log(1,32) ≈0,120574$
$B=15,63$ n'est pas dans la table, mais on a: $B=10×1,56$
Donc: $\log B=\log 10+\log 1,56=1+\log 1,56$
On se place sur la ligne 15 et dans la colonne 6 et on lit 0,193125. On peut donc conclure que
$\log 1,56≈0,193125$, et par là: $\log B≈1,193125$
Etape 2.
On calcule alors $\log A+\log B≈0,120574+1,193125≈1,313699$
Et comme $\log A+\log B=\log A×B$, on a $\log A×B≈1,313699$
Etape 3.
Ce nombre n'est pas dans la table.
En s'inspirant de la méthode vue ci-dessus, on pose: $A×B=10×p$, et donc: $\log A×B=1+\log p$
Et par là: $\log p≈0,313699$
Ce nombre n'est pas non plus dans la table, mais on a: $\log(2,05) ≈0,311754$ et $\log(2,06) ≈0,313867$
On en déduit que $p$ est compris entre $2,05$ et $2,06$, et qu'il semble plus proche de $2,06$.
D'où: $p≈2,06$, et par là, comme $A×B=10×p$, on a: $A×B≈20,6$
Or, à la calculatrice, on obtient: $A×B=20,592$ .
Les résultats sont donc très proches. La méthode est efficace, et les calculs prennent moins de temps qu'en utilisant l'algorithme de prosthaphérèse .
c.
 Multiplier $A=1,07$ par $B=0,138$ en s'inspirant de l'exemple précédent.
Multiplier $A=1,07$ par $B=0,138$ en s'inspirant de l'exemple précédent.
Corrigé
Partie A
Premier calcul
-
On a: $A=20,65461=0,206546×10^2$ et $B=518,922=0,518922×10^3$.
Donc $p=A ×B=10^{5}×a×b$ avec $a=0,206546$ et $b=0,518922$.
Donc $n=5$ - Table trigonométrique

Comme: $a=\sin α$ et $b=\sin β$, on obtient: $α≈11,92$ et $β≈31,26$
Noter que les valeurs des tables sont approchées. La méthode donnera des résultats approximatifs! - On obtient: $α-β≈-19,34$ et $α+β≈43,18$ (sans calculatrice!).
-
Donc, comme $\cos (-19,34)=\cos(19,34)$, on obtient: $\cos (α-β)≈0,943570$ (à l'aide de la table).
Par aileurs, on obtient: $\cos (α+β)≈0,729208$ (à l'aide de la table). -
On calcule alors: $\cos (α-β)-\cos (α+β)≈0,214362$ (toujours sans calculatrice!).
Puis: ${1}/{2}(\cos (α-β)-\cos (α+β))≈0,107181$ (toujours sans calculatrice!) -
Or, on sait que: $\sin α .\sin β={1}/{2}(\cos (α-β)-\cos (α+β))$
Donc: $\sin α .\sin β≈0,107181$
Soit: $a×b≈0,107181$
Et par là, comme $p=A ×B=10^5×a×b$, on obtient: $p≈10\,718,1$
A la calculatrice, on obtient: $p=20,65461×518,922=10\,718,13153$ .
Les résultats sont très proches, mais les calculs par prosthaphérèse prennent du temps.
Second calcul
Voici un autre extrait de table de sinus et de cosinus

Multiplions $A=7490,71$ par $B=26,2358$ en s'inspirant de l'exemple précédent.
On a: $A=0,749071×10^4$ et $B=0,262358×10^2$.
Donc $p=A ×B=10^{6}×a×b$ avec $a=0,749071$ et $b=0,262358$.
Donc $n=6$
Comme: $a=\sin α$ et $b=\sin β$, on obtient: $α≈48,51$ et $β≈15,21$
Puis: $α-β≈33,30$ et $α+β≈63,72$.
Donc, on obtient: $\cos (α-β)≈0,835807$ .
Par aileurs, on obtient: $\cos (α+β)≈0,442758$ .
On calcule alors: $\cos (α-β)-\cos (α+β)≈0,393049$).
Puis: ${1}/{2}(\cos (α-β)-\cos (α+β))≈0,1965245$ .
Or, on sait que: $\sin α .\sin β={1}/{2}(\cos (α-β)-\cos (α+β))$
Donc: $\sin α .\sin β≈0,1965245$
Soit: $a×b≈0,1965245$
Et par là, comme $p=A ×B=10^6×a×b$, on obtient: $p≈196524,5$
A la calculatrice, on obtient: $p=7490,71×26,2358=196524,7694$ .
Les résultats sont à nouveau très proches, mais les calculs par prosthaphérèse prennent du temps.
Partie B algorithme de Neper
a.
pour tous $a$ et $b$ strictement positifs, on a:
$\log a +\log b={\ln a}/{\ln 10}+{\ln a}/{\ln 10}={\ln a+\ln b}/{\ln 10}={\ln ab}/{\ln 10}=\log ab$ c.q.f.d.
b. $\log 1={\ln 1}/{\ln 10}={0}/{\ln 10}=0$
$log 10 ={\ln 10}/{\ln 10}=1$
Pour tout entier $n$, $log 10^n ={\ln 10^n}/{\ln 10}={n\ln 10}/{\ln 10}=n$
c. table de log

Tentons de multiplier $A=1,07$ par $B=0,138$ à l'aide de cette table.
Etape 1.
On se place dans la ligne 10 et dans la colonne 7 et on lit 0,029384. On peut donc conclure que
$\log A=\log(1,07) ≈0,029384$
$B=0,138$ n'est pas dans la table, mais on a: $B=10^{-1}×1,38$
Donc: $\log B=\log 10^{-1}+\log 1,38=-1+\log 1,38$
On se place dans la ligne 13 et dans la colonne 8 et on lit 0,139879. On peut donc conclure que
$\log 1,38≈0,139879$, et par là: $\log B≈-1+0,139879≈-0,860121$
Etape 2.
On calcule alors $\log A+\log B≈0,029384-0,860121≈-0,830737$
Et comme $\log A+\log B=\log A×B$, on a $\log A×B≈-0,830737$
Etape 3.
Ce nombre n'est pas dans la table.
Comme ci-dessus, on pose: $A×B=10^{-1}×p$, et donc: $\log A×B=-1+\log p$
Et par là: $\log p≈0,169263$
Ce nombre n'est pas dans la table, mais on a: $\log(1,47) ≈0,167317$ et $\log(1,48) ≈0,170262$
On en déduit que $p$ est compris entre $1,47$ et $1,48$, et qu'il semble plus proche de $1,48$.
D'où: $p≈1,48$, et par là, comme $A×B=10^{-1}×p$, on a: $A×B≈0,148$
Or, à la calculatrice, on obtient: $A×B=0,14766$ .
Les résultats sont donc très proches. La méthode semble plus rapide que la prosthaphérèse