 Limites de fonctions
Limites de fonctions
I Limites en $+∞$ ou en $-∞$
Limite infinie en $+∞$ ou en $-∞$
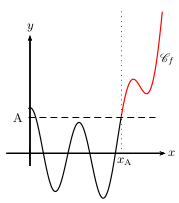
La fonction $f$ a pour limite $+∞$ en $+∞$ lorsque
tout intervalle du type $]A;+∞[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$
pour $x$ assez "grand".
On note $\lim↙{x→+∞}f(x)=+∞$.
La fonction $f$ a pour limite $-∞$ en $+∞$ lorsque
tout intervalle du type $]-∞;A[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$
pour $x$ assez "grand".
On note $\lim↙{x→+∞}f(x)=-∞$.
La fonction $f$ a pour limite $+∞$ en $-∞$ lorsque
tout intervalle du type $]A;+∞[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$
pour $x$ assez "négatif".
On note $\lim↙{x→-∞}f(x)=+∞$.
La fonction $f$ a pour limite $-∞$ en $-∞$ lorsque
tout intervalle du type $]-∞;A[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$
pour $x$ assez "négatif".
On note $\lim↙{x→-∞}f(x)=-∞$.
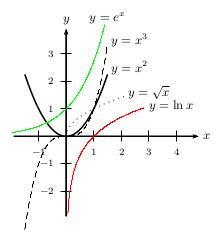
Limites de référence
$\lim↙{x→+∞}x=+∞$ $\lim↙{x→+∞}x^2=+∞$ $\lim↙{x→+∞}x^n=+∞$ (pour $n∈\ℕ$ et $n\text">"0$) $\lim↙{x→+∞}√{x}=+∞$
$\lim↙{x→-∞}x=-∞$ $\lim↙{x→-∞}x^2=+∞$ $\lim↙{x→-∞}x^3=-∞$
$\lim↙{x→+∞}e^x=+∞$ $\lim↙{x→+∞}{e^x}/{x}=+∞$ $\lim↙{x→+∞}{e^x}/{x^n}=+∞$ (pour $n∈\ℕ$)
Fonction vue en terminale
$\lim↙{x→+∞}\ln x=+∞$
Limite finie en $+∞$ ou en $-∞$
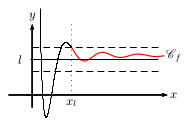
La fonction $f$ a pour limite $l$ en $+∞$ lorsque
tout intervalle ouvert contenant $l$ contient toutes les valeurs de $f(x)$
pour $x$ assez "grand".
On note $\lim↙{x→+∞}f(x)=l$.
On dit que, dans un repère, la droite $d$ d'équation $y=l$ est asymptote horizontale en $+∞$ à la courbe représentative $\C$ de $f$.
La fonction $f$ a pour limite $l$ en $-∞$ lorsque
tout intervalle ouvert contenant $l$ contient toutes les valeurs $f(x)$
pour $x$ assez "négatif".
On note $\lim↙{x→-∞}f(x)=l$.
On dit que, dans un repère, la droite $d$ d'équation $y=l$ est asymptote horizontale en $-∞$ à la courbe représentative $\C$ de $f$.
Fonction constante
Soit $l$ un nombre réel; si $f(x)=l$, alors $\lim↙{x→+∞}f(x)=\lim↙{x→-∞}f(x)=l$.
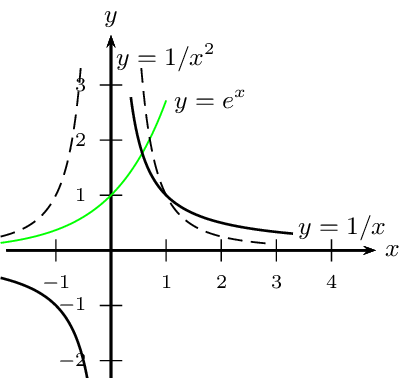
Limites de référence
$\lim↙{x→+∞}{1}/{x}=\lim↙{x→-∞}{1}/{x}=0$ $\lim↙{x→+∞}{1}/{x^2}=\lim↙{x→-∞}{1}/{x^2}=0$
$\lim↙{x→+∞}{1}/{x^n}=\lim↙{x→-∞}{1}/{x^n}=0$ (pour $n∈\ℕ$ et $n\text">"0$) $\lim↙{x→+∞}{1}/{\√{x}}=0$
$\lim↙{x→-∞}e^x=0$ $\lim↙{x→-∞}xe^x=0$ $\lim↙{x→-∞}x^n e^x=0$ (pour $n∈\ℕ$)
Fonction vue en terminale
$\lim↙{x→+∞}{\ln x}/{x}=0$
Unicité
Si elle existe, la limite d'une fonction en l'infini est unique.
II Limites en $a$
Limite infinie en un nombre réel $a$
La fonction $f$ a pour limite $+∞$ en $a$ lorsque
tout intervalle du type $]A;+∞[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$
pour $x$ assez "proche" de $a$.
On note $\lim↙{x→a}f(x)=+∞$.
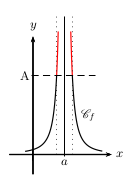
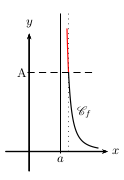
La fonction $f$ a pour limite $+∞$ à droite en $a$ lorsque
tout intervalle du type $]A;+∞[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$
pour $x$ assez "proche" de $a$ tout en restant supérieur à $a$.
On note $\lim↙{{}^{x→a}↙{x\text">"a}}f(x)=+∞$.
La fonction $f$ a pour limite $+∞$ à gauche en $a$ lorsque
tout intervalle du type $]A;+∞[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$
pour $x$ assez "proche" de $a$ en restant inférieur à $a$.
On note $\lim↙{{}^{x→a}↙{x\text"<"a}}f(x)=+∞$.
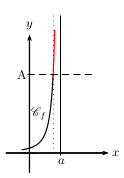
On définit de façon analogue une limite $-∞$ en $a$, à droite en $a$, ou à gauche en $a$.
Dans tous les cas précédents, on dit que, dans un repère, la droite $d$ d'équation $x=a$ est asymptote verticale en $a$ à la courbe représentative $\C$ de $f$.
Limites de référence
$\lim↙{{}^{x→0}↙{x\text">"0}}{1}/{x}=+∞$ $\lim↙{{}^{x→0}↙{x\text"<"0}}{1}/{x}=-∞$
$\lim↙{x→0}{1}/{x^2}=+∞$
Fonction vue en terminale
$\lim↙{x→0}\ln x=-∞$
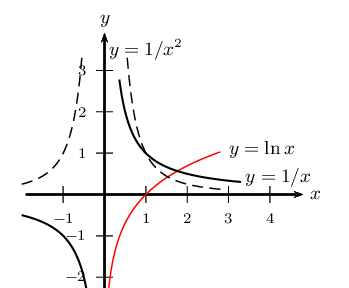
Exemple
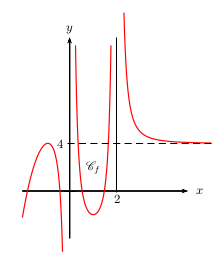
Conjecturer la valeur de chacune des limites suivantes
$\lim↙{x→+∞}f(x)$
$\lim↙{x→-∞}f(x)$
$\lim↙{{}^{x→0}↙{x\text"<"0}}f(x)$
$\lim↙{{}^{x→0}↙{x\text">"0}}f(x)$
$\lim↙{x→2}f(x)$
Donner, s'il y a lieu, l'équation réduite de l'asymptote associée.
Corrigé
$\lim↙{x→+∞}f(x)=4$, donc la droite d'équation $y=4$ est asymptote horizontale
en $+∞$ à $\C_f$.
$\lim↙{x→-∞}f(x)=-∞$
$\lim↙{{}^{x→0}↙{x\text"<"0}}f(x)=-∞$, donc la droite d'équation $x=0$ est asymptote verticale
à $\C_f$.
$\lim↙{{}^{x→0}↙{x\text">"0}}f(x)=+∞$, donc la droite d'équation $x=0$ est asymptote verticale
à $\C_f$.
$\lim↙{x→2}f(x)=+∞$, donc la droite d'équation $x=2$ est asymptote verticale
à $\C_f$.
Limite finie en un nombre réel $a$
La fonction $f$ a pour limite $l$ en $a$ lorsque
tout intervalle ouvert contenant $l$ contient toutes les valeurs de $f(x)$
pour $x$ assez "proche" de $a$.
On note $\lim↙{x→a}f(x)=l$.
Cette définition permet de définir d'une part la continuité,
d'autre part le nombre dérivé: $f\,'(a)=\lim↙{x→a}{f(x)-f(a)}/{x-a}=\lim↙{h→0}{f(a+h)-f(a)}/{h}$
Limites de référence
Elles s'obtiennent en appliquant la définition du nombre dérivé ci-dessus
(dérivée en 0 des fonctions $e^x$, $\ln(1+x)$ et $\sin x$).
$\lim↙{{x→0}↙{x≠0}}{e^x-1}/{x}=1$
Fonctions vue en terminale
$\lim↙{{x→0}↙{x≠0}}{\ln (1+x)}/{x}=1$
$\lim↙{{x→0}↙{x≠0}}{\sin x}/{x}=1$
Unicité
Si elle existe, la limite d'une fonction en $a$ est unique.
III Opérations et composées
Opérations
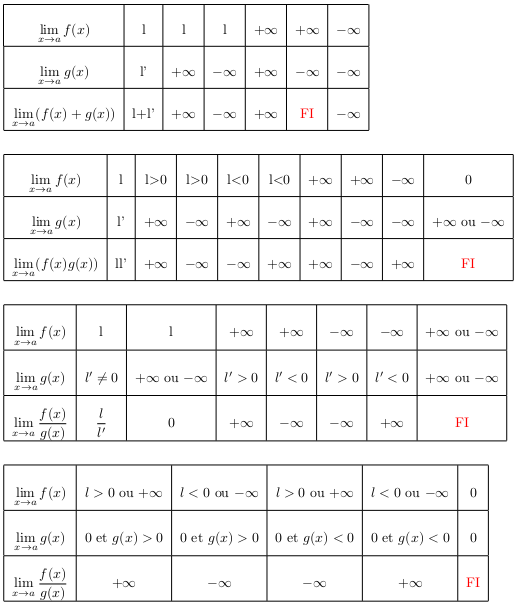
La détermination de la limite d'une somme, d'un produit ou d'un quotient de 2 fonctions est intuitive,
et vérifie les tableaux ci-dessous.
Dans ces tableaux, $a$ représente soit $+∞$, soit $-∞$, soit un nombre réel fixé.
Retenir essentiellement les formes indéterminées (notées FI), à traiter cas par cas (voir exemples).
Les méthodes utilisées pour déterminer les limites de suites se transposent aisément aux fonctions.
Savoir faire
En cas de forme indéterminée dans une recherche de limite, il est souvent opportun de factoriser le terme "dominant" (celui qui impose la limite), même si la factorisation est artificielle. (voir les exemples qui suivent).
 Exemples
Exemples
- Soit $f$ la fonction définie par $f(x)=(9x^2-x+1)√{x}$ pour tout réel $x$.
Déterminer $\lim↙{x→+∞}f(x)$. - Soit $g$ la fonction définie par $g(x)={-x^3+x^2}/{x-4}$ pour tout réel $x$ différent de $4$.
Déterminer $\lim↙{x→-∞}g(x)$. - Soit $h$ la fonction définie par $h(x)={3x-6}/{x^2+3x-10}$ pour tout réel $x$ différent de $2$ et de $-5$.
Déterminer $\lim↙{{}^{x→2}_{x≠2}}h(x)$.
Corrigé
- On obtient facilement $\lim↙{x→+∞}9x^2=+∞$ et $\lim↙{x→+∞}-x=-∞$, ce qui conduit à une forme indéterminée.
On factorise alors le terme "dominant" de la somme $9x^2-x+1$.
$9x^2-x+1=x^2(9-{1}/{x}+{1}/{x^2})$.
Or $\lim↙{x→+∞}x^2=+∞$ et $\lim↙{x→+∞}9-{1}/{x}+{1}/{x^2}=9-0+0=9$.
Donc $\lim↙{x→+∞}x^2(9-{1}/{x}+{1}/{x^2})=+∞$, soit $\lim↙{x→+∞}9x^2-x+1=+∞$.
Par ailleurs, on sait que $\lim↙{x→+∞}√{x}=+∞$.
On obtient donc finalement $\lim↙{x→+∞}f(x)=+∞$ (limite d'un produit). - On obtient facilement $\lim↙{x→-∞}-x^3+x^2=+∞$ et $\lim↙{x→-∞}x-4=-∞$, ce qui conduit à une forme indéterminée.
On factorise alors les termes "dominants" du quotient $g(x)$ et on simplifie.
$g(x)={x^3(-1+{1}/{x})}/{x^{}(1-4{}1/{x})}=x^2{-1+{1}/{x}}/{1-4{1}/{x}}$.
Or $\lim↙{x→-∞}x^2=+∞$ et $\lim↙{x→-∞}{-1+{1}/{x}}/{1-4{1}/{x}}={-1+0}/{1-4×0}=-1$.
Donc, comme $-1\text"<"0$, on obtient finalement $\lim↙{x→-∞}g(x)=-∞$ (limite d'un produit). - Numérateur et dénominateur tendent vers 0, ce qui conduit à une forme indéterminée.
On factorise alors les termes "dominants" du quotient $h(x)$ (il s'agit ici de $x-2$) et on simplifie. .
$h(x)={3(x-2)}/{(x-2)(x+5)}={3}/{x+5}$.
L'expression obtenue est celle d'une fonction continue en 2, ce qui permet de trouver facilement la limite.. .
On obtient alors finalement $\lim↙{{}^{x→2}_{x≠2}}h(x)={3}/{2+5}={3}/{7}$ (limite d'un quotient).
Composée
$a$, $b$ et $c$ désignent $+∞$, ou $-∞$, ou un nombre réel $a$.
Si $\lim↙{x→a}f(x)=b$ et si $\lim↙{y→b}g(y)=c$, alors $\lim↙{x→a}g(f(x))=c$
 Exemples
Exemples
Soit $h$ la fonction définie par $h(x)=√{x^2+{1}/{x^2}}$ pour tout réel $x$ non nul.
Déterminer $\lim↙{x→-∞}h(x)$.
Soit $m$ la fonction définie par $m(x)=e^{-3x+1}$ pour tout réel $x$.
Déterminer $\lim↙{x→+∞}m(x)$.
Soit $p$ la fonction définie par $p(x)=2xe^{-3x}$ pour tout réel $x$.
Déterminer $\lim↙{x→+∞}p(x)$.
Corrigé
On a $h(x)=g(f(x))$ avec $f(x)=x^2+{1}/{x^2}$, et $g(y)=√{y}$ (ici, $y=f(x)$)
Or, comme $\lim↙{x→-∞}x^2=+∞$ et $\lim↙{x→-∞}{1}/{x^2}=0$, on a $\lim↙{x→-∞}f(x)=+∞$.
De plus, $\lim↙{y→+∞}g(y)=+∞$.
Donc on obtient: $\lim↙{x→-∞}h(x)=+∞$.
La rédaction précédente est allégée ci-dessous...
$m(x)=e^{-3x+1}$
On a: $\lim↙{x→+∞}-3x+1=-∞$.
Or: $\lim↙{y→-∞}e^y=0$.
Donc: $\lim↙{x→+∞}m(x)=0$.
$p(x)=2xe^{-3x}$
On fait apparaître −3x devant l'exponentielle pour utiliser la limite de $ye^y$ en $−∞$
$p(x)={2}/{-3}×(-3x)×e^{-3x}$
On a: $\lim↙{x→+∞}-3x=-∞$.
Or: $\lim↙{y→-∞}ye^y=0$.
Donc: $\lim↙{x→+∞}(-3x)×e^{-3x}=0$.
Donc: $\lim↙{x→+∞}m(x)=-{2}/{3}×0=0$.
 Exemple
Exemple
Les plus aguerris peuvent retenir ce cas particulier.
Soit $k$ la fonction définie par $k(x)=√{x-3}-√{x+1}$ pour tout réel $x$ de $[3;+∞[$.
Déterminer $\lim↙{x→+∞}k(x)$.
Corrigé
Comme $\lim↙{x→+∞}x-3=+∞$ et $\lim↙{y→+∞}√{y}=+∞$, on a: $\lim↙{x→+∞}√{x-3}=+∞$.
De même, on obtient: $\lim↙{x→+∞}√{x+1}=+∞$.
Cela conduit à une forme indéterminée.
La présence d'une différence de racines carrées incite à utiliser la quantité conjuguée..
On a: $k(x)={(√{x-3}-√{x+1})(√{x-3}+√{x+1})}/{(√{x-3}+√{x+1})}$.
Soit: $k(x)={(x-3)-(x+1)}/{(√{x-3}+√{x+1})}$.
Soit: $k(x)={-4}/{√{x-3}+√{x+1}}$.
Or, comme $\lim↙{x→+∞}√{x-3}=+∞$ et $\lim↙{x→+∞}√{x+1}=+∞$, on a: .
$\lim↙{x→+∞}√{x-3}+√{x+1}=+∞$
Par ailleurs, on sait que $\lim↙{x→+∞}-4=-4$.
On obtient donc finalement $\lim↙{x→+∞}k(x)=0$ (limite d'un quotient).
IV Comparaisons
Théorème de comparaison
Si $\lim↙{x→+∞}f(x)=+∞$ et si, pour $x$ assez grand, $g(x)≥f(x)$,
alors $\lim↙{x→+∞}g(x)=+∞$.
Si $\lim↙{x→+∞}f(x)=-∞$ et si, pour $x$ assez grand, $g(x)≤f(x)$,
alors $\lim↙{x→+∞}g(x)=-∞$.
Ces deux propriétés s'étendent facilement pour des limites en $-∞$ ou en un réel $a$.
Théorème des gendarmes
Si $\lim↙{x→+∞}f(x)=l$ et si $\lim↙{x→+∞}h(x)=l$ et
si, pour $x$ assez grand, $f(x)≤g(x)≤h(x)$,
alors $\lim↙{x→+∞}g(x)=l$.
Cette propriété s'étend facilement pour des limites en $-∞$ ou en un réel $a$.
 Exemples
Exemples
- Soit $f$ la fonction définie par $f(x)=x^3+\cos x$ pour tout réel $x$.
Déterminer $\lim↙{x→+∞}f(x)$. - Soit $f$ la fonction définie par $f(x)=e^{x}\sin x$ pour tout réel $x$.
Déterminer $\lim↙{x→-∞}f(x)$.
Corrigé
- Pour tout réel $x$, on a: $-1≤\cos x$, et par là: $-1+x^3≤\cos x+x^3$.
Soit: pour tout réel $x$, $-1+x^3≤f(x)$.
Or, comme $\lim↙{x→+∞}x^3=+∞$ et $\lim↙{x→+∞}-1=-1$, on obtient: $\lim↙{x→+∞}-1+x^3=+∞$.
Donc, par comparaison, on obtient $\lim↙{x→+∞}f(x)=+∞$. - Pour tout réel $x$, on a: $-1≤\sin x≤1$.
Et par là: $-1×e^{x}≤\sin x×e^{x}≤1×e^{x}$ (comme $e^x>0$, le sens des inégalités ne change pas)
On a donc, pour tout $x$: $-e^x≤f(x)≤e^x$.
Or, $\lim↙{x→-∞}e^x=0$ et $\lim↙{x→-∞}-e^x=0$.
Donc, d'après le "théorème des gendarmes", on obtient: $\lim↙{x→-∞}f(x)=0$.